Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T16:28:29.519Z Has data issue: false hasContentIssue false
  • English
  • Français

The local Hölder exponent for the dimension of invariant subsets of the circle

Published online by Cambridge University Press:  08 March 2016

CARLO CARMINATI  and
GIULIO TIOZZO
CARLO CARMINATI
Affiliation:
Dipartimento di Matematica, Università di Pisa, Largo Pontecorvo 5, 56127 Pisa, Italy email [email protected]
GIULIO TIOZZO
Affiliation:
Yale University, 10 Hillhouse Avenue, New Haven, CT 06511, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider for each $t$ the set 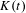$K(t)$ of points of the circle whose forward orbit for the doubling map does not intersect 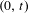$(0,t)$, and look at the dimension function 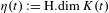$\unicode[STIX]{x1D702}(t):=\text{H.dim}\,K(t)$. We prove that at every bifurcation parameter $t$, the local Hölder exponent of the dimension function equals the value of the function 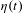$\unicode[STIX]{x1D702}(t)$ itself. A similar statement holds for general expanding maps of the circle: namely, we consider the topological entropy of the map restricted to the survival set, and obtain bounds on its local Hölder exponent in terms of the value of the function.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 6 , September 2017 , pp. 1825 - 1840
Copyright
© Cambridge University Press, 2016 

References

Bandtlow, O. F. and Rugh, H. H.. Entropy-continuity for interval maps with holes, Preprint, 2015,arXiv:1510.06043.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional dynamics. Ergebnisse der Mathematik und ihrer Grenzgebiete (3). Springer, Berlin, 1993, p. 25.Google Scholar
Dettmann, C.. Open circle maps: small hole asymptotics. Nonlinearity 26(1) (2013), 307–317.CrossRefGoogle Scholar
Guckenheimer, J.. The growth of topological entropy for one-dimensional maps. Global theory of dynamical systems (Proc. Internat. Conf., Northwestern Univertsity, Evanston, IL., 1979) (Lecture Notes in Mathematics, 819) . Springer, Berlin, 1980, pp. 216–223.CrossRefGoogle Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Isola, S. and Politi, A.. Universal encoding for unimodal maps. J. Stat. Phys. 61(1–2) (1990), 263–291.CrossRefGoogle Scholar
Keller, G. and Liverani, C.. Rare events, escape rates and quasistationarity: some exact formulae. J. Stat. Phys. 135(3) (2009), 519–534.Google Scholar
Lothaire, M.. Combinatorics on words. Encyclopedia of Mathematics and its Applications. Addison-Wesley, Reading, MA, 1983, 17.Google Scholar
Milnor, J. and Thurston, W.. On iterated maps of the interval. Dynamical systems (College Park, MD, 1986–1987) (Lecture Notes in Mathematics, 1342) . Springer, Berlin, 1988, pp. 465–563.Google Scholar
Moran, M.. Hausdorff measure of infinitely generated self-similar sets. Monatsh. Math. 122(4) (1996), 387–399.Google Scholar
Nilsson, J.. On numbers badly approximable by dyadic rationals. Israel J. Math. 171 (2009), 93–110.Google Scholar
Tiozzo, G.. Topological entropy of quadratic polynomials and dimension of sections of the Mandelbrot set. Adv. Math. 273 (2015), 651–715.CrossRefGoogle Scholar
Tiozzo, G.. Continuity of core entropy of quadratic polynomials. Invent. Math. (2015), to appear. doi:10.1007/s00222-015-0605-9.Google Scholar
Urbański, M.. On Hausdorff dimension of invariant sets for expanding maps of a circle. Ergod. Th. & Dynam. Sys. 6(2) (1986), 295–309.CrossRefGoogle Scholar
Young, L. S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2(1) (1982), 109–124.Google Scholar