Hostname: page-component-6bf8c574d5-86b6f Total loading time: 0 Render date: 2025-03-09T14:41:17.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic continuation of holonomy germs of Riccati foliations along Brownian paths

Published online by Cambridge University Press:  11 April 2016

NICOLAS HUSSENOT DESENONGES
NICOLAS HUSSENOT DESENONGES*
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, Ilha do Fundao, 68530, CEP 21941-970, Rio de Janeiro, RJ, Brasil email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a Riccati foliation whose monodromy representation is non-elementary and parabolic and consider a non-invariant section of the fibration whose associated developing map is onto. We prove that any holonomy germ from any non-invariant fibre to the section can be analytically continued along a generic Brownian path. To prove this theorem, we prove a dual result about complex projective structures. Let $\unicode[STIX]{x1D6F4}$ be a hyperbolic Riemann surface of finite type endowed with a branched complex projective structure: such a structure gives rise to a non-constant holomorphic map 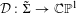${\mathcal{D}}:\tilde{\unicode[STIX]{x1D6F4}}\rightarrow \mathbb{C}\mathbb{P}^{1}$, from the universal cover of $\unicode[STIX]{x1D6F4}$ to the Riemann sphere 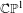$\mathbb{C}\mathbb{P}^{1}$, which is $\unicode[STIX]{x1D70C}$-equivariant for a morphism 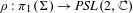$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6F4})\rightarrow \mathit{PSL}(2,\mathbb{C})$. The dual result is the following. If the monodromy representation $\unicode[STIX]{x1D70C}$ is parabolic and non-elementary and if 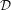${\mathcal{D}}$ is onto, then, for almost every Brownian path $\unicode[STIX]{x1D714}$ in 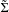$\tilde{\unicode[STIX]{x1D6F4}}$, ${\mathcal{D}}(\unicode[STIX]{x1D714}(t))$ does not have limit when $t$ goes to 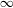$\infty$. If, moreover, the projective structure is of parabolic type, we also prove that, although 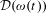${\mathcal{D}}(\unicode[STIX]{x1D714}(t))$ does not converge, it converges in the Cesàro sense.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 6 , September 2017 , pp. 1887 - 1914
Copyright
© Cambridge University Press, 2016 

References

Alvarez, S.. Mesures de Gibbs et mesures harmoniques pour les feuilletages aux feuilles courbées négativement. Thése de doctorat, Université de Dijon, 2013, tel-00958080.Google Scholar
Ahlfors, L.. Finitely generated Kleinian groups. Amer. J. Math. 86 (1964), 413–429.CrossRefGoogle Scholar
Alvarez, S. and Hussenot, N.. Singularities for analytic continuation of holonomy germs of Riccati foliations. Ann. Inst. Fourier (Grenoble) to appear. Preprint, 2014, arXiv:1406.0977.Google Scholar
Arnold, L.. Random Dynamical Systems. Springer Science and Business Media, Berlin, 2013.Google Scholar
Brunella, M.. Birational Theory of Foliations (Monografías de Matemática) . IMPA, Rio de Janeiro, 2000.Google Scholar
Ballmann, W. and Ledrappier, F.. Discretization of positive harmonic functions on Riemannian manifolds and Martin boundary. Actes de la table ronde de géométrie différentielle (Luminy, 1992) (Séminaires et Congrès, 1) . Société de Mathématique, France, Paris, 1996, pp. 77–92.Google Scholar
Bougerol, P. and Lacroix, J.. Products of Random Matrices with Applications to Schrödinger Operators (Progress in Probability and Statistics, 8) . Birkhäuser, Boston, 1985.CrossRefGoogle Scholar
Barth, W., Peters, C. and Van de Ven, A.. Compact complex surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete. Springer, Berlin, 1984.Google Scholar
Calsamiglia, G., Guillot, A., Deroin, B. and Frankel, S.. Singular sets of holonomy maps for algebraic foliations. J. Eur. Math. Soc. (JEMS) 15(3) (2013), 1067–1099.CrossRefGoogle Scholar
Deroin, B. and Dujardin, R.. Complex projective structures: Lyapunov exponent, degree and harmonic measure. Preprint, 2013, arXiv:1308.0541 [math.GT].Google Scholar
Deroin, B. and Dujardin, R.. Lyapunov exponent for surface groups: bifurcation currents. Commun. Math. Phys. to appear. Preprint, 2013, arXiv:1305.0049.Google Scholar
Dodziuk, J.. Every covering of a compact Riemann surface of genus greater than one carries a non trivial L 2 harmonic differential. Acta Math. 152(1) (1984), 49–56.CrossRefGoogle Scholar
Dumas, D.. Complex Projective Structures (Handbook of Teichmuller Theory, 2) . European Mathematical Society, Zurich, 2009, pp. 455–508.Google Scholar
Furstenberg, H.. Noncommuting random products. Trans. Amer. Math. Soc. 108 (1963), 377–428.CrossRefGoogle Scholar
Furstenberg, H.. Random walks and discrete subgroups of Lie groups. Adv. Probab. Relat. Top. 1 (1971), 1–63.Google Scholar
Heijal, D.. Monodromy groups and linearly polymorphic functions. Acta Math. 135 (1975), 1–55.CrossRefGoogle Scholar
Hussenot, N.. Mouvement Brownien appliqué à l’étude de la dynamique des feuilletages transversalement holomorphes. Thèse de doctorat, l’Université de Nantes, tel-00874410.Google Scholar
Il’Yashenko, Yu.. Some open problems in real and complex dynamics. Nonlinearity 21(7) (2008), 101–107.CrossRefGoogle Scholar
Kaimanovich, V.. Discretization of bounded harmonic functions on Riemannian manifolds and entropy. Proceedings of the International Conference on Potential Theory. Ed. Nagoya, M. K.. De Gruyter, Berlin, 1992, pp. 212–223.Google Scholar
Karlsson, A. and Ledrappier, F.. Propriété de Liouville et vitesse de fuite du mouvement Brownien. C. R. Acad. Sci. Paris, Sér. 1 344 (2007), 685–690.CrossRefGoogle Scholar
Loray, F.. Sur les théorémes 1 et 2 de Painlevé (Contemporary Mathematics, 389) . American Mathematical Society, Providence, RI, 2005, pp. 165–190.Google Scholar
Lévy, P.. Processus stochastiques et mouvement Brownien. Gauthier-Villars, Paris, 1948.Google Scholar
Lyons, T. and Sullivan, D.. Function theory, random paths and covering spaces. J. Differential Geom. 19 (1984), 299–323.CrossRefGoogle Scholar
Myrberg, P. J.. Die Kapazitat der Singularen Menge der Linearen Gruppen. Ann. Acad. Sci. Fenn. Ser. A. I. 10 (1941).Google Scholar
Prat, J. J.. Etude asymptotique et convergence angulaire du mouvement Brownien sur une variété à courbure négative. C. R. Acad. Sci. Paris Sér. A-B 22 (1975), 1539–1542.Google Scholar
Sullivan, D.. Quasiconformal homeomorphisms and dynamics: structure stability implies hyperbolicity for Kleinian groups. Acta Math. 155 (1985), 243–250.CrossRefGoogle Scholar
Woess, W.. Boundaries of random walks on graphs and groups with infinitely many ends. Israel J. Math. 3 (1989), 271–301.CrossRefGoogle Scholar