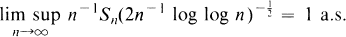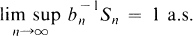Research Article
On Difference Operators and their Factorization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 873-897
-
- Article
-
- You have access
- Export citation
Some Congruences for Generalized Euler Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 687-709
-
- Article
-
- You have access
- Export citation
The Metric Fuglede Property and Normality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 516-525
-
- Article
-
- You have access
- Export citation
On Integration in Partially Ordered Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 353-372
-
- Article
-
- You have access
- Export citation
Algebraic Inner Derivations on Operator Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 710-723
-
- Article
-
- You have access
- Export citation
λ-Mappings Between Representation Rings of Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 898-960
-
- Article
-
- You have access
- Export citation
On the Structure and Tensor Products of JC-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1059-1074
-
- Article
-
- You have access
- Export citation
New Lattice Packings of Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-130
-
- Article
-
- You have access
- Export citation
Some Results on L-Indistinguishability for SL(r)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1075-1109
-
- Article
-
- You have access
- Export citation
Behrend's Theorem for Dense Subsets of Finite Vector Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 724-734
-
- Article
-
- You have access
- Export citation
Rings with Enough Invertible Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-144
-
- Article
-
- You have access
- Export citation
Central Double Centralizers on Quasi-Central Banach Algebras with Bounded Approximate Identity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-384
-
- Article
-
- You have access
- Export citation
Generalized Euler Number Sequences: Asymptotic Estimates and Congruences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-546
-
- Article
-
- You have access
- Export citation
Uniform Approximation by Polynomials with Variable Exponents
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-557
-
- Article
-
- You have access
- Export citation
The Poisson Integral of a Singular Measure
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-749
-
- Article
-
- You have access
- Export citation
Three Theorems on the Growth of Entire Transcendental Solutions of Algebraic Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1110-1128
-
- Article
-
- You have access
- Export citation
Weighted and Subsequential Ergodic Theorems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-166
-
- Article
-
- You have access
- Export citation
Sufficiency of Weierstrass Jets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-176
-
- Article
-
- You have access
- Export citation
Obtaining Prescribed Rates of Convergence for the Ergodic Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1129-1146
-
- Article
-
- You have access
- Export citation
Homomorphism-Compact Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 558-576
-
- Article
-
- You have access
- Export citation






 is zero unless
is zero unless  for
for  . Leeming and MacLeod
. Leeming and MacLeod 
 , and
, and  , and they made several conjectures which may be stated as follows:
, and they made several conjectures which may be stated as follows:



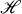 , that
, that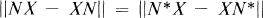
 is a complex simple Lie algebra of type
is a complex simple Lie algebra of type  be a Cartan subalgebra of
be a Cartan subalgebra of 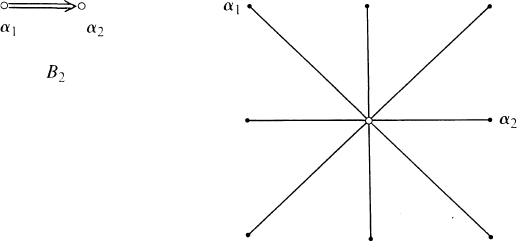
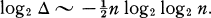

 be the Weyl group of
be the Weyl group of  . It follows from a recent work of James Arthur
. It follows from a recent work of James Arthur 


 in the notation of [
in the notation of [ there exists
there exists  such that if
such that if  ,
, 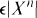 elements (that is,
elements (that is,  ), then
), then 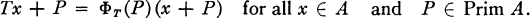
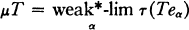
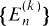 one for each positive integer
one for each positive integer 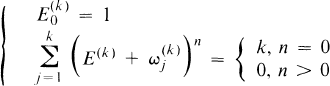
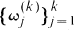 are the
are the 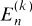 after multiplying out. We note that (1.1) implies
after multiplying out. We note that (1.1) implies 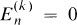 ,
, 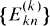 by showing that
by showing that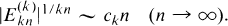
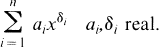
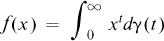


 almost everywhere with respect to Lebesgue measure on
almost everywhere with respect to Lebesgue measure on  almost everywhere
almost everywhere 
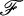 ,
, 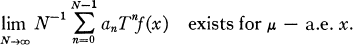

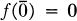 . Two maps
. Two maps 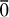 , if at
, if at 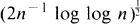 in the sense that
in the sense that