Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:11:52.353Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted and Subsequential Ergodic Theorems

Published online by Cambridge University Press:  20 November 2018

J. R. Baxter  and
J. H. Olsen
J. R. Baxter
Affiliation:
University of Minnesota, Minneapolis, Minnesota
J. H. Olsen
Affiliation:
North Dakota State University, Fargo, North Dakota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

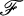1. Introduction. Let (X, , μ) be a probability space, T a linear operator on ℒp(X, 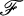, μ), for some p, 1 ≦ p ≦ ∞. Let an be a sequence of complex numbers, n = 0, 1, …, which we shall often refer to as weights. We shall say that the weighted pointwise ergodic theorem holds for T on ℒp, if, for every ƒ in ℒp,

1.1

Let a denote the sequence (an). If (1.1) holds we shall say that a is Birkhoff for T on ℒp, or, more briefly, that (a, T) is Birkhoff.

We are also interested in ergodic theorems for subsequences. Let n(k) be a subsequence. We shall say the pointwise ergodic theorem holds for the subsequence n(k) and the operator T if, for every ƒ in ℒp,

1.2

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 1 , 01 February 1983 , pp. 145 - 166
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Akcoglu, M. A., A pointwise ergodic theorem in Lp-spaces, Can. J. Math. 27 (1975), 1975–1982.Google Scholar
2. Akcoglu, M. A. and Sucheston, L., Dilations of positive contractions on Lp-spaces, Can. J. Math. Bull. 20 (1977), 285–292.Google Scholar
3. Bellow, A., Ergodic properties of isometries in Lp-spaces, 1 < p < °°, Bull. A.M.S. 70 (1964), 366–371.Google Scholar
4. Blum, J. R. and Cogburn, R., On ergodic sequences of measures, Proc. A.M.S. 51 (1975), 359–365.Google Scholar
5. Blum, J. R. and Reich, J. E., p-sets for random walks, Z. Wahrscheinlichkeitstheorie and Verw. Gebiete 48 (1979), 193–200.Google Scholar
6. Brunei, A. and Keane, M., Ergodic theorems for operator sequences, Z. Wahrscheinlichkeitstheorie and Verw. Gebiete 12 (1969), 231–240.Google Scholar
7. de la Torre, A., A simple proof of the maximal ergodic theorem, Can. J. Math. 28 (1976), 1073–1075.Google Scholar
8. Dunford, N. and Schwartz, J., Linear operators I (John Wiley, New York, 1958).Google Scholar
9. Kan, C., Ergodic properties of Lamperti operators, Can. J. Math. 80 (1978), 1206–1214.Google Scholar
10. Halmos, P. and Von Neumann, J., Operator methods in classical mechanics II, Annals of Math. 43 (1942), 333–350.Google Scholar
11. Olsen, J. H., Akcoglu's ergodic theorem for uniform sequences, Can. J. Math. 32 (1980), 880–884.Google Scholar
12. Olsen, J. H., The individual weighted ergodic theorem for bounded Besicovitch sequences, Can. Bull. Math. 25 (1982), 468–471.Google Scholar
13. Olsen, J. H., The individual ergodic theorem for Lamperti contractions, C. R. Math. Rep. Acad. Sci. Canada 3 (1981), 113–118.Google Scholar
14. Ornstein, D. S. and Shields, P. C., Mixing Markov shifts of kernel type are Bernoulli, Adv. Math. 10 (1973), 143–146.Google Scholar
15. Reich, J. I., On the individual ergodic theorem for subsequences, Annals of Prob. 5 (1977), 1039–1046.Google Scholar
16. Ryll-Nardzewski, C., Topics in ergodic theory, in Proceedings of the Winter School in Probability, Karpacz, Poland, 131-156, Lecture Notes in Mathematics 472 (Springer-Verlag, Berlin 1975).Google Scholar
17. Sato, R., Operator averages for subsequences, Math. J. of Okayama University 22 (1980).Google Scholar