No CrossRef data available.
Article contents
Sufficiency of Weierstrass Jets
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
1. Introduction. Let C(r+1)(2, 1) be the set of all (r + 1)-time continuously differentiable mappings f: R2 → R with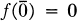 
. Two maps f and g ∈ C(r+1)(2, 1) are said to be equivalent of order r at 
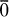, if at 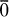, their Taylor expansions up to and including the terms of degree ≦ r are identical. An r-jet, denoted j(r)(f), is the equivalence class of f with f being called a realization of j(r)(f). The set of all r-jets is denoted Jr(2, 1).
Definition. An r-jet Z ∈ Jr(2, 1) is called C0-sufficient (in C(r+1)(2, 1)), if for any two C(r+1)(2, 1) functions f, g which realize Z, there exists a local homeomorphism h: R2 → R2, for which f(h(x, y)) = g(x, y) in a neighborhood of 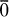. I.e., the following diagram commutes.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1983
References
1.
Kuo, T. C., A complete determination of c°-sufficiency in Jr(2, 1), Invent. Math.
8 (1969), 226–235.Google Scholar
2.
Kuo, T. C. and Lu, Y. C., On analytic function germs of two complex variables,
Topology
16 (1977), 299–310.Google Scholar
3.
Lu, Y. C., Sufficiency of jets in Jr(2, 1) via decomposition,
Inv. Math.
10 (1970), 119–127.Google Scholar
4.
Lu, Y. C., Singularity theory and an introduction to catastrophe theory (Springer-Ver lag, N.Y., 1976).Google Scholar
5.
Yu, Y. C. and Chang, S. H., On c°-sufficiency of complex jets,
Can. J. Math.
4 (1973), 874–880.Google Scholar
You have
Access