Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:42:12.616Z Has data issue: false hasContentIssue false
  • English
  • Français

On Difference Operators and their Factorization

Published online by Cambridge University Press:  20 November 2018

Patrick J. Browne  and
R. V. Nillsen
Patrick J. Browne
Affiliation:
The University of Calgary, Calgary, Alberta
R. V. Nillsen
Affiliation:
The University of Wollongong, Wollongong, New South Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper A will be used to denote a given set and g a permutation of it. We shall assume that there is a subset C ⊆ A so that

1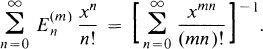

Here Z denotes the set of integers. For x ∈ A it now follows that there is an unique α(x) ∈ Z so that

2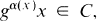

and then also

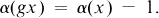
In general we shall be concerned with solving the following equation for u

3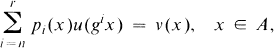

where pi, n ≤ i ≤ r, and v are given real valued functions on A and pnpr does not vanish on A. For B ⊆ A, F(B) will denote the set of all real valued functions defined on B.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 873 - 897
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. L., Brand, Differentia/ and difference equations (John Wiley, New York, 1966).Google Scholar
2. P. J., Browne and Nillsen, R. V., The two sided factorization of ordinary differential operators, Can. J. Math. 32 (1980), 1045–1057,Google Scholar
3. Casorati, P., II calcolo delle differenze finite interpretato ed accresauto di nuovi teoremi a sussidio principalmente delle odierne recerche basata sulla variabilita complessa, Annali de Math. Pura ed Applicat, Ser. 2, 10 (1880-1882), 10–43.Google Scholar
4. Hill, J. M. and Nillsen, R. V., Mutually conjugate solutions of formally self adjoint differential equations, Proc. Roy. Soc. Edin. A, 83 (1979), 93–101.Google Scholar
5. Miller, K. S., An introduction to the calculus of finite differences and difference equations (Holt, New York, 1960; Dover, New York, 1966).Google Scholar
6. Miller, K. S., Linear difference equations (Benjamin, New York, 1968).Google Scholar
7. Miller, K. S., On linear difference equations, Amer. Math. Monthly 75 (1968), 630–632.Google Scholar
8. Milne-Thomson, L. M., The calculus of finite differences (Macmillan, London, 1933).Google Scholar
9. Zettl, A., Factorization of differential operators, Proc. Amer. Math. Soc. 27 (1971), 425–426.Google Scholar
10. Zettl, A., General theory of the factorization of ordinary linear differential operators, Trans. Amer. Math. Soc. 197 (1974), 341–353.Google Scholar