Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:08:54.857Z Has data issue: false hasContentIssue false
  • English
  • Français

Obtaining Prescribed Rates of Convergence for the Ergodic Theorem

Published online by Cambridge University Press:  20 November 2018

G. L. O'Brien
G. L. O'Brien*
Affiliation:
York University, Downsview, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {Yn, n ∊ Z} be an ergodic strictly stationary sequence of random variables with mean zero, where Z denotes the set of integers. For n ∊ N = {1, 2, …}, let Sn = Y1 + Y2 + … + Yn. The ergodic theorem, alias the strong law of large numbers, says that n–lSn → 0 as n → ∞ a.s. If the Yn's are independent and have variance one, the law of the iterated logarithm tells us that this convergence takes place at the rate 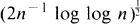in the sense that

1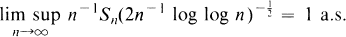

It is our purpose here to investigate what other rates of convergence are possible for the ergodic theorem, that is to say, what sequences {bn, n ≧ 1} have the property that

2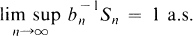

for some ergodic stationary sequence {Yn, n ∊ Z}.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 6 , 01 December 1983 , pp. 1129 - 1146
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Aaronson, J., An ergodic theorem with large normalizing constants, Israel J. Math. 38 (1981), 182–188.Google Scholar
2. Friedman, N. A., Introduction to ergodic theory (Van Nostrand, New York, 1970).Google Scholar
3. Halasz, G., Remarks on the remainder in Birkhoffs ergodic theorem. Acta. Math. Acad. Sci. Hung. 28 (1976), 389–395.Google Scholar
4. Halmos, P. A., Lectures in ergodic theory (The Math. Soc, Japan, Tokyo, 1956).Google Scholar
5. Ibragimov, I. A., Some limit theorems for stationary processes, Theor. Probability Appl. 7 (1962), 349–382.Google Scholar
6. Kakutani, S. and Petersen, K., The speed of convergence in the ergodic theorem, Mh. Math. 91 (1981), 11–18.Google Scholar
7. Kesten, H., Sums of stationary processes cannot grow slower than linearly, Proc. A.M.S. 49 (1966), 205–211.Google Scholar
8. Krengel, U., On the speed of convergence in the ergodic theorem, Mh. Math. 86 (1978), 3–6.Google Scholar
9. O'Brien, G. L. and Vervaat, W., Self similar processes with stationary increments generated by point processes, Report 576. School of Operations Research and Industrial Engineering, Cornell University (1983).Google Scholar
10. Walters, P., Ergodic theory — introductory lectures, Lecture Notes in Math. 458 (Springer-Verlag, Berlin, 1975).CrossRefGoogle Scholar