Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:00:59.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Behrend's Theorem for Dense Subsets of Finite Vector Spaces

Published online by Cambridge University Press:  20 November 2018

T. C. Brown  and
J. P. Buhler
T. C. Brown
Affiliation:
Simon Fraser University, Burnaby, British Columbia
J. P. Buhler
Affiliation:
Reed College, Portland, Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The “combinatorial line conjecture” states that for all q ≧ 2 and there exists 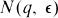such that if 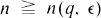, X is a q-element set, and A is any subset of X n (= cartesian product of n copies of X) with more than 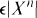elements (that is, A has density greater than ), then A contains a combinatorial line. (For a definition of combinatorial line, together with statements and proofs of many results related to the combinatorial line conjecture, including all those results mentioned below, see [5]. Since we are not directly concerned with combinatorial lines in this paper, we do not reproduce the definition here.)

This conjecture (which is a strengthened version of a conjecture of Moser [7]), if true, would bear the same relation to the Hales-Jewett theorem that Szemerédi's theorem bears to van der Waerden's theorem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 4 , 01 August 1983 , pp. 724 - 734
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Brown, T. C. and Buhler, J. P., A density version of a geometric Ramsey theorem, J. Combin. Theory Ser. A 32 (1982), 20–34.Google Scholar
2. Brown, T. C. and Buhler, J. P., Lines imply spaces in density Ramsey theory, to appear.CrossRefGoogle Scholar
3. Brown, T. C., Behrend's theorem for sequences containing no k-element arithmetic progression of a certain type, J. Combin. Theory Ser. A 18 (1975), 352–356.Google Scholar
4. Behrend, F. A., On sequences of integers containing no arithmetic progression, Casopis Mat. Fys. Praha (Cast Mat.) 67 (1938), 235–239.Google Scholar
5. Graham, R. L., Rothschild, B. L. and Spencer, J. H., Ramsey theory (John Wiley and Sons, New York, New York, 1980).Google Scholar
6. Hales, A. W. and Jewett, R. I., Regularity and positional games, Trans. Amer. Math. Soc. 106 (1963), 222–229.Google Scholar
7. Moser, L., Problem 170, Can. Math. Bull. 13 (1970), 268.Google Scholar
8. Spencer, J. H., Ramsey's theorem for spaces, Trans. Amer. Math. Soc. 249 (1979), 363–371.Google Scholar
9. Szemerédi, E., On sets of integers containing no k elements in arithmetic progression, Acta Arith. 27 (1975), 199–245.Google Scholar