After defining a generalized C-fraction (a kind of Jacobi-Perron algorithm) for an n-tuple of formal power series over 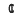(n ≥ 2), the connection between interruptions in the algorithm and linear dependence over 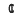[x] of the power series is studied.

Examples will be given showing that the algorithm behaves in a way similar to the Jacobi-Perron algorithm for an n-tuple of real numbers (the gcd-algorithm): there do exist n-tuples of formal power series f(1), f(2), …, f(n) with a C-n-fraction without interruptions but for which 1, f(1), f(2), …, f(n) is nevertheless linearly dependent over 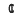[x].

Moreover an example will be given of algebraic functions f, g of degree n over 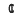[x] (formally defined) for which the C-n-fraction for f, f2, …, fn has just one interruption and that for g, g2, …, gn 1 none, while of course 1. f, f2, …, fn and 1, g, g2, …, gn admit (only) one dependence relation over [x].

The object of this paper is to establish some relations between two generalized Nörlund methods and also between two absolute generalized Nörlund methods. Our theorems obtained here generalize many known results, including McFadden's Theorems which state the inclusion relations between two absolute Nörlund methods, and results of Ikuko Kayashima.

Applying a new and very elegant method of proof of the Schur-Hardy inequality, given by E.R. Love at the Oberwolfach conference on Linear Spaces and Approximation (1977), norm estimates of integral operators with homogeneous kernels are established in the setting of abstract function norms. Applications to Flett's inequality, to integral means, and to fractional integrals are given.

It has been shown by W.F. LaMartin that the Pontryagin dual of a k-space product of Hausdorff abelian k-groups is the coproduct of their duals. Here we offer a different proof, based partly on LaMartin's, that the dual of a product is the coproduct of the duals in a more general setting.

A refinement of the Newton-Kantorovich Theorem, which has many-potential applications in existence - uniqueness theory, is used to strengthen a result of Lancaster and Rokne concerning existence and uniqueness regions for zeros of operator polynomials.

Using the notions of orthogonality in normed linear spaces such as isosceles, pythagorean, and Birkhoff-James orthogonality, in this paper we provide some new characterizations of inner product spaces besides giving simpler proofs of existing similar characterizations. In addition we prove that in a normed linear space pythagorean orthogonality is unique and that isosceles orthogonality is unique if and only if the space is strictly convex.

The local connectivity, νk(G), of a graph G is the minimum of the connectivities of neighbourhoods of the vertices of G. G is minimally locally n-connected if νk(G) = n and for every edge x of G, νk(G−x) = n − 1. A necessary and sufficient condition for a locally connected graph to be minimally locally 1-connected is given, and it is shown that for n ≥ 7, is minimally locally 1-connected.

Let Cφ be a composition operator on L2(λ), where λ is a σ-finite measure on a set X. Conditions under which Cφ is invertible, unitary, and normal are investigated in this paper.

A new construction of regeneration times is exploited to prove ergodic and renewal theorems for semi-Markov processes on general state spaces. This work extends results of the authors in Ann. Probability (6 (1978), 788–797).

A new class of algebraic systems known as loop near-rings are introduced, which includes near-rings and consequently rings. Different types of radicals are introduced in a loop near-ring N which coincide with the Jacobson radical when N happens to be a ring, and several characterizations of these radicals are obtained.

Necessary and sufficient conditions on an arbitrary Gabriel filter of left ideals of a ring R are determined in order that the ring of quotients of R with respect to the filter be semi-simple artinian. Special instances include generalizations of earlier work on classical rings of quotients and maximal rings of quotients.

In this paper we study the existence and uniqueness of solutions for the following complex nonlinear complementarity problem: find z ∈ S such that g(z) ∈ S* and re(g(z), z) = 0, where S is a closed convex cone in Cn, S* the polar cone, and g is a continuous function from Cn into itself. We show that the existence of a z ∈ S with g(z) ∈ int S* implies the existence of a solution to the nonlinear complementarity problem if g is monotone on S and the solution is unique if g is strictly monotone. We also show that the above problem has a unique solution if the mapping g is strongly monotone on S.

Let V denote the symmetric monoidal closed category of limit-space abelian groups and let L denote the full subcategory of locally compact Hausdorff abelian groups. Results of Samuel Kaplan on extension of characters to products of L–groups are used to show that each closed subgroup of a product of L-groups is a limit of L–groups. From this we deduce that the limit closure of L in V is reflective in V and has every group Pontryagin reflexive with respect to the structure of continuous convergence on the character groups. The basic duality L ≃ Lop is then extended.

Let p be a prime and let (mk)k<ω be a strictly increasing sequence of positive integers such that m0 = 1 and mk divides mk+1. A field F is said to be of type (p, (mk)k<ω) if it is the union of an increasing sequence (Fk)k<ω of fields such that Fk has pmk elements. A set X is called “finite” if it has n elements for some nonnegative integer n, and “Dedekind-finite” if every injection f: X → X is a bijection. If the Axiom of Choice is rejected, then it is relatively consistent to assume the existence of medial (that is, infinite, Dedekind-finite) sets. In this paper it is shown that given any type (p, (mk)k<ω) as above, it is relatively consistent with the usual axioms of set theory (minus Choice) to assume the existence of a medial field of type (p, (mk)k<ω). Conversely, it is shown that any medial field must be of type (p, (mk)k<ω) for some (p, (mk)k<ω) as above. The paper concludes with a few observations on Dedekind-finite rings. In the first part of the paper, a general knowledge of Fraenkel-Mostowski set theory and of the Jech-Sochor Embedding Theorems is assumed.

In a single-server queueing system, subject to the queue discipline ‘First come first served’, the equilibrium distribution function of the waiting time of a server depends on the distribution of the random variable (u) which is the difference between the service time and the inter-arrival time. If in two queueing systems u's are equivalent in distribution, the waiting times are also equivalent in distribution (known result). It has been shown in this note that equivalence in waiting time distributions does not necessarily imply equivalence in distributions of u's. The proof is heuristic. This result has useful practical implications.

In this present paper we shall prove the following. Suppose that λ1, λ2, λ3 are any non-zero real numbers not all of the same sign and that λ1/λ2 is irrational. If η is any real number and, 0 < α < 1/9, then there are infinitely many prime triples (p1, p2, p3) for which

An algebraic formulation of the density theorem for loop near-rings is presented, which generalizes the same result for near-rings.