In a recent note [1], Arkeryd presents a counterexample to my conjecture [2]. The same example appears in a preprint by von Grudzinski [3], who also points out that the corollary to Theorem 2 does not follow from the proof of the theorem as stated. The fact that x3 + xy3 and x3 + xy3y3 are right equivalent, but not under quasi-identity, provides a counterexample. The proof on p. 170 of [2] that 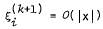 is also incorrect. In order to establish this result, we note that, from equation (31), it suffices to show that ξ(0, t) = 0 for all t. But, from equation (30), f(ξ(0, t)) = 0. If now 0 is an isolated zero of f, we are done. If not, we may assume ξ(0, t) = 0 without loss of generality. The corollary to Theorem 4 shows that this latter case is, in fact, vacuous.
is also incorrect. In order to establish this result, we note that, from equation (31), it suffices to show that ξ(0, t) = 0 for all t. But, from equation (30), f(ξ(0, t)) = 0. If now 0 is an isolated zero of f, we are done. If not, we may assume ξ(0, t) = 0 without loss of generality. The corollary to Theorem 4 shows that this latter case is, in fact, vacuous.