Published online by Cambridge University Press: 17 April 2009
After defining a generalized C-fraction (a kind of Jacobi-Perron algorithm) for an n-tuple of formal power series over 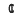 (n ≥ 2), the connection between interruptions in the algorithm and linear dependence over
(n ≥ 2), the connection between interruptions in the algorithm and linear dependence over 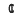 [x] of the power series is studied.
[x] of the power series is studied.
Examples will be given showing that the algorithm behaves in a way similar to the Jacobi-Perron algorithm for an n-tuple of real numbers (the gcd-algorithm): there do exist n-tuples of formal power series f(1), f(2), …, f(n) with a C-n-fraction without interruptions but for which 1, f(1), f(2), …, f(n) is nevertheless linearly dependent over 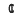 [x].
[x].
Moreover an example will be given of algebraic functions f, g of degree n over 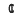 [x] (formally defined) for which the C-n-fraction for f, f2, …, fn has just one interruption and that for g, g2, …, gn 1 none, while of course 1. f, f2, …, fn and 1, g, g2, …, gn admit (only) one dependence relation over
[x] (formally defined) for which the C-n-fraction for f, f2, …, fn has just one interruption and that for g, g2, …, gn 1 none, while of course 1. f, f2, …, fn and 1, g, g2, …, gn admit (only) one dependence relation over  [x].
[x].