This paper is concerned with the almost sure convergence for arrays of independent, but not necessarily identically distributed, random variables. We show that Kolmogorov's law of the iterated logarithm does not hold for arrays and obtain an analogue of Kolmogorov's law.

We give several results dealing with denseness of certain classes of norms with many vertex points. We prove that, in Banach spaces with the Mazur or the weak* Mazur intersection property, every ball (convex body) can be uniformly approximated by balls (convex bodies) being the closed convex hull of their strongly vertex points. We also prove that given a countable set F, every norm can be uniformly approximated by norms which are locally linear at each point of F.

Let (fn) be a sequence of positive P-integrable functions such that (∫ fndP)n converges. We prove that (fn) converges in measure to if and only if equality holds in the generalised Fatou's lemma. Let f∞ be an integrable function such that (∥fn − f∞∥1)n converges. We present in terms of the modulus of uniform integrability of (fn) necessary and sufficient conditions for (fn) to converge in measure to f∞.

In this paper we provide an algebraic definition for the Schouten product and give a decomposition for homogeneous Poisson structures in any n-dimensional vector space. A large class of n-homogeneous Poisson structures in ℝk is also characterised.

We shall give an elementary proof of a characterisation for the Bloch space due to Holland and Walsh, and obtain analogous characterisations for the little Bloch space and Besov spaces of analytic functions on the unit disk in the complex plane.

A thrifty embedding scheme of an arbitrary set of groups in a simple infinite group with a given outer automorphism group is presented. One of the applications of this scheme is the existence (assuming CH) of an uncountable group G in which all proper subgroups are countable such that G contains every countable group.

A foliation on a Riemannian manifold (M, g) is harmonic if all the leaves are minimal submanifolds. We give a new characterisation of the harmonicity of a foliation on (M, g) by the harmonicity of an associated bundle map of (T M, gC), where gC is the complete lift metric of g to the tangent bundle as introduced by Yano and Ishihara.

In this note we deal with the following problem: given a nonempty closed convex subset X of Rn and two multifunctions Γ : X → 2X and , to find ( such that

We prove a very general existence result where neither Γ nor Φ are assumed to be upper semicontinuous. In particular, our result give a positive answer to an open problem raised by the first author recently.

A diagonal condition is defined which internally characterises those Cauchy spaces which have topological completions. The T2 diagonal Cauchy spaces allow both a finest and a coarsest T2 diagonal completion. The former is a completion functor, while the latter preserves uniformisability and has an extension property relative to θ-continuous maps.

In this paper, we study a family of elliptic curves with CM by which also admits a ℚ-rational isogeny of degree 3. We find a relation between the Selmer groups of the elliptic curves and the ambiguous ideal class groups of certain cubic fields. We also find some bounds for the dimension of the 3-Selmer group over ℚ, whose upper bound is also an upper bound of the rank of the elliptic curve.

A ring R is said to be an E-ring if the map R → of E (R)+ into the ring of endomorphisms of its additive group via a ↪ al = left multiplication by a, is an isomorphism. In this note torsion free rings R for which the group Rl, of left multiplication maps by elements of R, is a full subgroup of E(R)+ will be considered. These rings are called TE-rings. It will be shown that TE-rings satisfy many properties of E-rings, and that unital TE-rings are E-rings. If R is a TE-ring, then E(R+) is an E-ring, and E(R+)+ / is bounded. Some results concerning additive groups of TE-rings will be obtained.

Let (S, +) be a semigroup and (H, +) be a group (neither necessarily commutative). Suppose that J ⊂ 2s is a proper ideal in S such that

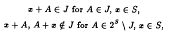
and Ω(J) = {M ⊂ S2 : there exists U(M)∈ J with M [x] ∈ J for x ∈ S/U(M)}, where M[x] = {y ∈ S : (y, x) ∈ M}. We show that if f : S → H is a function satisfying

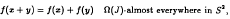
then there exists exactly one additive function F : S → H with F(x) = f(x) J-almost everywhere in S.

We also prove some results concerning regularity of the function F.

We estimate the genus of the modular curves X1(N).

Let E be a normed space, a Fréchet space or a complete (DF)-space satisfying the dual density condition. Let Ω be a Radon measure space. We prove that a function f: Ω → Eis Bochner p-integrable if (and only if) fis p-integrable with respect to the topology of uniform convergence on the norm-null sequences from E′.

We calculate the dimensions of using Erokhin's work on Niemeier lattices and geometric methods involving the hyperelliptic locus.

Some existence theorem for solutions of two kinds of differential inclusions with monotone type mappings in Hilbert spaces are given.

The ranges of the Y-integral transform in some spaces of functions are described.

We give a bound for the number of generators for groups of exponent p depending on the rank of the centre when centre and commutator subgroup coincide, provided that the group is isomorphic to the quotient group modulo the centre of some group.