Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-12T05:47:44.385Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalised quasi-variational inequality without upper semicontinuity

Published online by Cambridge University Press:  17 April 2009

Paolo Cubiotti  and
Xian-Zhi Yuan
Paolo Cubiotti
Affiliation:
Department of Mathematics, University of Messina, 98166 Sant' Agata-Messina, Italy
Xian-Zhi Yuan
Affiliation:
Department of Mathematics, The University of Queensland, Brisbane Qld 4072, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we deal with the following problem: given a nonempty closed convex subset X of Rn and two multifunctions Γ : X → 2X and 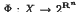, to find ( 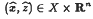such that

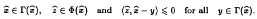
We prove a very general existence result where neither Γ nor Φ are assumed to be upper semicontinuous. In particular, our result give a positive answer to an open problem raised by the first author recently.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 54 , Issue 2 , October 1996 , pp. 247 - 254
Copyright
Copyright © Australian Mathematical Society 1996

References

REFERENCES

[1]Aubin, J.P., Optima and equilibria (Springer-Verlag, Berlin, Heidelberg, New York, 1993).CrossRefGoogle Scholar
[2]Brézis, H., Nirenberg, L. and Stampacchia, G., ‘A remark on Ky Fan's minimax principle’, Boll. Un. Mat. Hal. 6 (1972), 293–300.Google Scholar
[3]Chan, D. and Pang, J.S., ‘The generalized quasi-variational inequality problem’, Math. Oper. Res. 7 (1982), 211–222.CrossRefGoogle Scholar
[4]Cubiotti, P., ‘An existence theorem for generalized quasi-variational inequalities’, Set- Valued Anal. 1 (1993), 81–87.CrossRefGoogle Scholar
[5]Cubiotti, P., ‘A note on Chan and Pang's existence theorem for generalized quasi-variational inequalities’, Appl. Math. Lett. 9 (1996), 73–76.CrossRefGoogle Scholar
[6]Cubiotti, P., ‘An application of quasi-variational inequalities to linear control systems’, J. Optim. Theory Appl. 89 (1996), 101–113.CrossRefGoogle Scholar
[7]De Luca, M. and Maugeri, A., ‘Quasi-variational inequalities and applications to equilibrium problems with elastic demand’, in Nonsmooth Optimization and Related Topics, (Clarke, F.H., Dem'yanov, V.F. and Giannessi, F., Editors), Ettore Majorana International Science Series (Plenum Press, 1989).Google Scholar
[8]De Luca, M. and Maugeri, A., ‘Discontinuous quasi-variational inequalities and applications to equilibrium problemsin’, in Nonsmooth Optimization. Methods and Applications, (Giannessi, F., Editor) (Gordon and Breach Sc. Publ., London, Tokyo, 1992).Google Scholar
[9]Ekeland, I. and Temam, R., Analyse convexe et problemes variationnels (Dunod, Paris, 1974).Google Scholar
[10]Harker, P.T. and Pang, J.S., ‘Finite-dimensional variational inequality and nonlinear complementarity problems: A survey of theory, algorithms and applications’, Math. Programming 48 (1990), 161–220.CrossRefGoogle Scholar
[11]Klein, E. and Thompson, A.C., Theory of correspondences (John Wiley and Sons, New York, 1984).Google Scholar
[12]Michael, E., ‘Continuous selections I’, Ann. of Math. 63 (1956), 361–382.CrossRefGoogle Scholar
[13]Ricceri, O. Naselli, ‘On the covering dimension of the fixed point set of certain multifunctions’, Comment Math. Univ. Carolin. 32 (1991), 281–286.Google Scholar
[14]Tarafdar, E. and Yuan, X. Z., ‘Non-compact generalized quasi-variational inequalities in locally convex topological vector spaces’, Nonlinear World 1 (1994), 373–383.Google Scholar
[15]Yen, N.D., ‘On an existence theorem for generalized quasi-variational inequalities’, Set-Valued Anal. 3 (1995), 1–10.CrossRefGoogle Scholar
[16]Yuan, X.Z., Contributions to nonlinear analysis, Ph.D. dissertation (Department of Mathematics, Statistics and Computing Science, Dalhousie University, 1994).Google Scholar