Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Freitag, Eberhard
and
Oura, Manabu
2001.
A theta relation in genus 4.
Nagoya Mathematical Journal,
Vol. 161,
Issue. ,
p.
69.
Poor, Cris
and
Yuen, David S.
2001.
The dyadic trace and odd weight computations for Siegel modular cusp forms.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 2,
p.
269.
Poor, Cris
and
Yuen, David S.
2002.
Restriction of Siegel modular forms to modular curves.
Bulletin of the Australian Mathematical Society,
Vol. 65,
Issue. 2,
p.
239.
Poor, Cris
and
Yuen, David S.
2003.
Slopes of integral lattices.
Journal of Number Theory,
Vol. 100,
Issue. 2,
p.
363.
POOR, Cris
and
YUEN, David S.
2007.
Computations of spaces of Siegel modular cusp forms.
Journal of the Mathematical Society of Japan,
Vol. 59,
Issue. 1,
OURA, MANABU
POOR, CRIS
and
YUEN, DAVID S.
2008.
TOWARDS THE SIEGEL RING IN GENUS FOUR.
International Journal of Number Theory,
Vol. 04,
Issue. 04,
p.
563.
Gaberdiel, Matthias R
and
Volpato, Roberto
2009.
Higher genus partition functions of meromorphic conformal field theories.
Journal of High Energy Physics,
Vol. 2009,
Issue. 06,
p.
048.
OURA, Manabu
and
OZEKI, Michio
2016.
A NUMERICAL STUDY OF SIEGEL THETA SERIES OF VARIOUS DEGREES FOR THE 32-DIMENSIONAL EVEN UNIMODULAR EXTREMAL LATTICES.
Kyushu Journal of Mathematics,
Vol. 70,
Issue. 2,
p.
281.
Terras, Audrey
2016.
Harmonic Analysis on Symmetric Spaces—Higher Rank Spaces, Positive Definite Matrix Space and Generalizations.
p.
337.
Chenevier, Gaëtan
and
Lannes, Jean
2019.
Automorphic Forms and Even Unimodular Lattices.
p.
245.
Chenevier, Gaëtan
and
Lannes, Jean
2019.
Automorphic Forms and Even Unimodular Lattices.
p.
123.
Chenevier, Gaëtan
and
Lannes, Jean
2019.
Automorphic Forms and Even Unimodular Lattices.
p.
1.


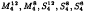 using Erokhin's work on Niemeier lattices and geometric methods involving the hyperelliptic locus.
using Erokhin's work on Niemeier lattices and geometric methods involving the hyperelliptic locus.