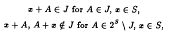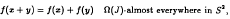Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BRZDȨK, JANUSZ
2008.
CONTINUITY OF MEASURABLE HOMOMORPHISMS.
Bulletin of the Australian Mathematical Society,
Vol. 78,
Issue. 1,
p.
171.
Brzdęk, Janusz
2008.
On solutions of a generalization of the Reynolds functional equation.
Demonstratio Mathematica,
Vol. 41,
Issue. 4,
Fechner, Włodzimierz
2013.
On a composite functional equation satisfied almost everywhere.
Indagationes Mathematicae,
Vol. 24,
Issue. 1,
p.
103.
Brzdȩk, Janusz
2013.
Remarks on hyperstability of the Cauchy functional equation.
Aequationes mathematicae,
Vol. 86,
Issue. 3,
p.
255.
BRZDĘK, JANUSZ
and
JABŁOŃSKA, ELIZA
2017.
ON EXTENSIONS OF THE GENERALISED JENSEN FUNCTIONS ON SEMIGROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 96,
Issue. 1,
p.
110.
Bahyrycz, A.
Brzdęk, J.
and
Jabłońska, E.
2020.
On extensions of the generalized quadratic functions from “large” subsets of semigroups.
Semigroup Forum,
Vol. 100,
Issue. 2,
p.
383.