Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T17:24:34.038Z Has data issue: false hasContentIssue false
  • English
  • Français

The Selmer groups and the ambiguous ideal class groups of cubic fields

Published online by Cambridge University Press:  17 April 2009

Yen-Mei J. Chen
Yen-Mei J. Chen
Affiliation:
Department of Mathematics, Tamkang University, Tamshui, Taipei 25137, Taiwan, Republic of China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

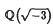In this paper, we study a family of elliptic curves with CM by which also admits a ℚ-rational isogeny of degree 3. We find a relation between the Selmer groups of the elliptic curves and the ambiguous ideal class groups of certain cubic fields. We also find some bounds for the dimension of the 3-Selmer group over ℚ, whose upper bound is also an upper bound of the rank of the elliptic curve.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 54 , Issue 2 , October 1996 , pp. 267 - 274
Copyright
Copyright © Australian Mathematical Society 1996

References

REFERENCES

[1]Cassels, J.W.S., ‘Arithmetic on Curves of Genus 1’, J. Reine Angew. Math. 217 (1965), 180–199.Google Scholar
[2]Frey, G., ‘Die Klassgruppe Quadratischer und Kubischer Zahlkörper und die Selmer Gruppen Gewisser Elliptische Kurven‘, Manuscripta Math. 16 (1975), 333–362.CrossRefGoogle Scholar
[3]Gerth, F., ’On 3-class groups of pure cubic fields’, J. Reine Angew. Math. 278/279 (1975), 52–62.Google Scholar
[4]Nekevář, J., ‘Class number of quadratic fields and Shimura's correspondence’, Math. Ann. 287 (1990), 577–594.CrossRefGoogle Scholar
[5]Tate, J., ‘Algorithm for determining the type of a singular fiber in an elliptic pencil’, in Lecture Notes Mathematics 476 (Springer-Verlag, Berlin, Heidelberg, New York, 1975), pp. 33–52.Google Scholar