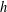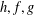234 results in 03BXX
Semantics of higher inductive types
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 17 June 2019, pp. 159-208
- Print publication:
- July 2020
-
- Article
- Export citation
Multisets in type theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 27 March 2019, pp. 1-18
- Print publication:
- July 2020
-
- Article
- Export citation
NEW GENERALIZED
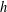 $h$-IMPLICATIONS
$h$-IMPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 276-286
-
- Article
-
- You have access
- Export citation
DNR AND INCOMPARABLE TURING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 06 April 2016, e7
-
- Article
-
- You have access
- Open access
- Export citation
Equivalences in Euler-based diagram systems through normal forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 431-484
-
- Article
-
- You have access
- Export citation
ASPECTS OF GLOBULAR HIGHER CATEGORY THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 19 May 2014, pp. 172-173
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A SIMPLE ALGORITHM FOR DEDUCTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 1 / July 2009
- Published online by Cambridge University Press:
- 09 March 2010, pp. 102-122
-
- Article
-
- You have access
- Export citation
Perfect effect algebras are categorically equivalent with Abelian interpolation po-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-207
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Free algebras in varieties of BL-algebras generated by a BLn-chain
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-439
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Loomis-Sikorski theorem for monotone σ-complete effect algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-318
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Central elements and Cantor-Bernstein's theorem for pseudo-effect algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-144
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Pseudo MV-algebras are intervals in ℓ-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 427-446
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Loomis-sikorski theorem for σ-complete MV-algebras and ℓ-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-277
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
A lambda calculus with naive substitution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-282
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation