Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T11:00:36.141Z Has data issue: false hasContentIssue false
  • English
  • Français

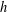NEW GENERALIZED $h$-IMPLICATIONS

Part of: Algebraic logic General logic

Published online by Cambridge University Press:  24 May 2017

D. PEI Open the ORCID record for D. PEI [Opens in a new window]  and
Y. ZHU
D. PEI*
Affiliation:
Department of Mathematics, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected], [email protected]
Y. ZHU
Affiliation:
Department of Mathematics, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A new generalized class of fuzzy implications, called (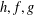$h,f,g$)-implications, is introduced and discussed in this paper. The results show that the new fuzzy implications possess some good properties, such as the left neutrality property and the exchange principle.

Keywords

fuzzy implicationh-implicationf-generated implicationg-generated implication

MSC classification

Primary: 03B50: Many-valued logic
Secondary: 03B52: Fuzzy logic; logic of vagueness 03G10: Lattices and related structures
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 3-4 , April 2017 , pp. 276 - 286
Copyright
© 2017 Australian Mathematical Society 

References

Baczyński, M. and Jayaram, B., “Yager’s classes of fuzzy implications: some properties and intersections”, Kybernetika 43 (2007) 157–182; http://eudml.org/doc/33849.Google Scholar
Baczyński, M. and Jayaram, B., Fuzzy implications (Springer, Berlin, 2008); doi:10.1007/978-3-540-69082-5.Google Scholar
Dubois, D. and Prade, H., “Fuzzy sets in approximate reasoning (I)”, Fuzzy Sets Syst. 40 (1991) 143–202; doi:10.1016/0165-0114(91)90050-Z.Google Scholar
Fodor, J. and Torrens, J., “An overview of fuzzy logic connectives on the unit interval”, Fuzzy Sets Syst. 281 (2015) 183–187; doi:10.1016/j.fss.2015.05.016.Google Scholar
Gottwald, S., A treatise on many-valued logics, Volume 9 of Studies in Logic and Computation (Research Studies Press Ltd, Baldock, 2001).Google Scholar
Hilnena, D., Kalina, M. and Kral, P., “A class of implications related to Yager’s $f$ -implications”, Inform. Sci. 260 (2014) 171–184; doi:10.1016/j.ins.2013.09.045.Google Scholar
Liu, H. W., “A new class of fuzzy implications derived from generalized $h$ -generators”, Fuzzy Sets Syst. 24 (2013) 63–92; doi:10.1016/j.fss.2012.11.022.Google Scholar
Mas, M., Monserrat, M., Torrens, J. and Trillas, E., “A survey on fuzzy implications functions”, IEEE Trans. Fuzzy Syst. 15 (2007) 1107–1121; doi:10.1109/TFUZZ.2007.896304.Google Scholar
Massanet, S. and Torrens, J., “On the characterization of Yager’s implications”, Inform. Sci. 201 (2012) 1–18; doi:10.1016/j.ins.2012.03.008.Google Scholar
Massanet, S. and Torrens, J., “On a new class of fuzzy implications: $h$ -implications and generalizations”, Inform. Sci. 181 (2014) 2111–2127; doi:10.1016/j.ins.2011.01.030.CrossRefGoogle Scholar
Pei, D., “ $R_{0}$ implication: characteristics and applications”, Fuzzy Sets Syst. 131 (2002) 297–302; doi:10.1016/S0165-0114(02)00053-2.Google Scholar
Pei, D., “The unified algorithms of triple I methods for fuzzy reasoning”, Inform. Sci. 178 (2008) 520–530; doi:10.1016/j.ins.2007.09.003.CrossRefGoogle Scholar
Wang, G. J., “On the logic foundation of fuzzy reasoning”, Inform. Sci. 117 (1999) 47–88; doi:10.1016/S0020-0255(98)10103-2.Google Scholar
Xie, A. F. and Liu, H. W., “A generalization of Yager’s $f$ -generated implications”, Internat. J. Approx. Reason. 54 (2013) 35–46; doi:10.1016/j.ijar.2012.08.005.Google Scholar
Yager, R. R., “On some new classes of implication operators and their role in approximate reasoning”, Inform. Sci. 167 (2004) 193–216; doi:10.1016/j.ins.2003.04.001.Google Scholar
Zhu, Y. and Pei, D., “On the characterizations of D-implications”, Fuzzy Syst. Math. 29 (2015) 88–98.Google Scholar