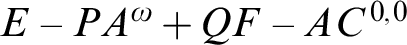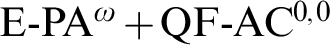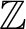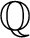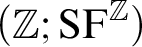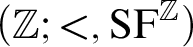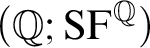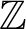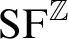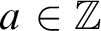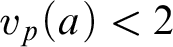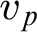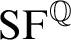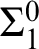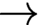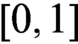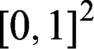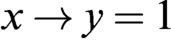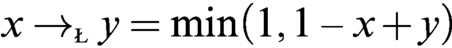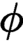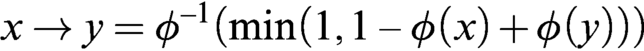239 results in 03BXX
THE CHARACTERIZATION OF WEIHRAUCH REDUCIBILITY IN SYSTEMS CONTAINING
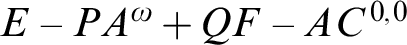 $E-PA^{\omega } + QF-AC^{0,0}$
$E-PA^{\omega } + QF-AC^{0,0}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 224-261
- Print publication:
- March 2021
-
- Article
- Export citation
DOING WITHOUT ACTION TYPES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 380-410
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPLORING THE LANDSCAPE OF RELATIONAL SYLLOGISTIC LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 728-765
- Print publication:
- September 2021
-
- Article
- Export citation
SEMANTICS FOR PURE THEORIES OF CONNEXIVE IMPLICATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 591-606
- Print publication:
- September 2022
-
- Article
- Export citation
PROBABILISTIC STABILITY, AGM REVISION OPERATORS AND MAXIMUM ENTROPY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 553-590
- Print publication:
- September 2022
-
- Article
- Export citation
THE ADDITIVE GROUPS OF
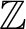 $\mathbb {Z}$
AND
$\mathbb {Z}$
AND 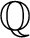 $\mathbb {Q}$
WITH PREDICATES FOR BEING SQUARE-FREE
$\mathbb {Q}$
WITH PREDICATES FOR BEING SQUARE-FREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1324-1349
- Print publication:
- December 2021
-
- Article
- Export citation
DECIDABILITY OF ADMISSIBILITY: ON A PROBLEM BY FRIEDMAN AND ITS SOLUTION BY RYBAKOV
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1-38
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RELATIONSHIPS BETWEEN COMPUTABILITY-THEORETIC PROPERTIES OF PROBLEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 47-71
- Print publication:
- March 2022
-
- Article
- Export citation
WHAT THE ŁUKASIEWICZ AXIOMS MEAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 906-917
- Print publication:
- September 2020
-
- Article
- Export citation
CATEGORICAL SEMANTICS OF METRIC SPACES AND CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1044-1078
- Print publication:
- September 2020
-
- Article
- Export citation
THE POTENTIAL IN FREGE’S THEOREM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 August 2020, pp. 553-577
- Print publication:
- June 2023
-
- Article
- Export citation
A TWO-DIMENSIONAL LOGIC FOR TWO PARADOXES OF DEONTIC MODALITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2020, pp. 991-1022
- Print publication:
- December 2022
-
- Article
- Export citation
ON THE INVARIANCE OF GÖDEL’S SECOND THEOREM WITH REGARD TO NUMBERINGS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 22 July 2020, pp. 51-84
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LOGIC OF SEQUENCE FRAMES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 July 2020, pp. 101-132
- Print publication:
- March 2022
-
- Article
- Export citation
TRANSMISSION OF VERIFICATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 866-881
- Print publication:
- December 2021
-
- Article
- Export citation
THE MODAL LOGIC OF STEPWISE REMOVAL
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 July 2020, pp. 36-63
- Print publication:
- March 2022
-
- Article
- Export citation
EXCEPTIONAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 85-111
- Print publication:
- March 2021
-
- Article
- Export citation
TWO LEVEL CREDIBILITY-LIMITED REVISIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 21 July 2020, pp. 388-408
- Print publication:
- June 2022
-
- Article
- Export citation
CUT-FREE COMPLETENESS FOR MODULAR HYPERSEQUENT CALCULI FOR MODAL LOGICS K, T, AND D
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 910-929
- Print publication:
- December 2021
-
- Article
- Export citation
EPISTEMIC MULTILATERAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 21 July 2020, pp. 505-536
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation