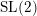 $\text{SL}(2)$,
$\text{SL}(2)$, 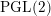 $\text{PGL}(2)$ over the pair of pants
$\text{PGL}(2)$ over the pair of pants
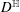 $D^{\mathbb{H}}$ Domains
$D^{\mathbb{H}}$ Domains
 $K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION
$K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION
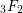 $_{3}F_{2}$
$_{3}F_{2}$
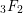 $_{3}F_{2}$
$_{3}F_{2}$
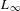 $L_{\infty }$ SPACES
$L_{\infty }$ SPACES