Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T18:53:35.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular Interpretation of a Non-Reductive Chow Quotient

Part of: Families, fibrations Cycles and subschemes

Published online by Cambridge University Press:  27 February 2018

Patricio Gallardo  and
Noah Giansiracusa
Patricio Gallardo
Affiliation:
William Chauvenet Lecturer, Department of Mathematics, Washington University, St. Louis MO, USA ([email protected])
Noah Giansiracusa
Affiliation:
Assistant Professor, Department of Mathematics and Statistics, Swarthmore College, Swarthmore PA, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space of n distinct points and adisjoint parametrized hyperplane in projective d-space up to projectivity – equivalently, configurations of n distinct points in affine d-space up to translation and homothety – has a beautiful compactification introduced by Chen, Gibney and Krashen. This variety, constructed inductively using the apparatus of Fulton–MacPherson configuration spaces, is a parameter space of certain pointed rational varieties whose dual intersection complex is a rooted tree. This generalizes 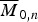$\overline M _{0,n}$ and shares many properties with it. In this paper, we prove that the normalization of the Chow quotient of (ℙd)n by the diagonal action of the subgroup of projectivities fixing a hyperplane, pointwise, is isomorphic to this Chen–Gibney–Krashen space Td, n. This is a non-reductive analogue of Kapranov's famous quotient construction of 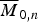$\overline M _{0,n}$, and indeed as a special case we show that 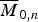$\overline M _{0,n}$ is the Chow quotient of (ℙ1)n−1 by an action of 𝔾m ⋊ 𝔾a.

Keywords

Chow quotientstable treesnon-reductive

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes) 14D20: Algebraic moduli problems, moduli of vector bundles
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 2 , May 2018 , pp. 457 - 477
Copyright
Copyright © Edinburgh Mathematical Society 2018 

References

1.Alexeev, V., Moduli of weighted hyperplane arrangements (ed. Bini, G., Lahoz, M., Macrì, E. and Stellari, P.), Advanced Courses in Mathematics – CRM Barcelona (Birkhäuser/Springer, Basel, 2015).Google Scholar
2.Bruno, A. and Mella, M., The automorphism group of , J. Eur. Math. Soc. (JEMS) 15(3) (2013), 949–968.Google Scholar
3.Castravet, A.-M. and Tevelev, J., is not a Mori dream space, Duke Math. J. 164(8) (2015), 1641–1667.Google Scholar
4.Chen, L., Gibney, A. and Krashen, D., Pointed trees of projective spaces, J. Algebraic Geom. 18(3) (2009), 477–509.CrossRefGoogle Scholar
5.Doran, B. and Giansiracusa, N., Projective linear configurations via non-reductive actions (arXiv:1401.0691; 2014).Google Scholar
6.Doran, B., Giansiracusa, N. and Jensen, D., A simplicial approach to effective divisors in , Int. Math. Res. Notices 2 (2017), 529–565.Google Scholar
7.Doran, B. and Kirwan, F., Towards non-reductive geometric invariant theory, Pure Appl. Math. Q. 3 (2007), 61–105.Google Scholar
8.Fulton, W. and MacPherson, R., A compactification of configuration spaces, Ann. of Math. (2) 139(1) (1994), 183–225.Google Scholar
9.Gerritzen, L., Herrlich, F. and Put, M. van der, Stable n-pointed trees of projective lines, Indag. Math. (N.S.) 50(2) (1988), 131–163.CrossRefGoogle Scholar
10.Giansiracusa, N., Conformal blocks and rational normal curves, J. Algebraic Geom. 22 (2013), 773–793.Google Scholar
11.Giansiracusa, N. and Gillam, W. D., On Kapranov's description of as a Chow quotient, Turkish J. Math. 38(4) (2014), 625–648.Google Scholar
12.Gibney, A. and Maclagan, D., Equations for Chow and Hilbert quotients, Algebra Number Theory 4(7) (2010), 855–885.CrossRefGoogle Scholar
13.Hacking, P., Keel, S. and Tevelev, J., Compactification of the moduli space of hyperplane arrangements, J. Algebraic Geom. 15(4) (2006), 657–680.Google Scholar
14.Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, Volume 52 (Springer-Verlag, New York, 1977).Google Scholar
15.Hu, Y., Toric degenerations of GIT quotients, Chow quotients, and , Asian J. Math. 12(1) (2008), 47–53.Google Scholar
16.Kapranov, M., Chow quotients of Grassmannians. I, In I. M. Gelfand seminar, Advances in Soviet Mathematics, Volume 16, pp. 29–110 (American Mathematical Society, Providence, RI, 1993).Google Scholar
17.Kapranov, M., Veronese curves and Grothendieck-Knudsen moduli space , J. Algebraic Geom. 2(2) (1993), 239–262.Google Scholar
18.Kapranov, M. M., Sturmfels, B. and Zelevinsky, A. V., Quotients of toric varieties, Math. Ann. 290(4) (1991), 643–655.Google Scholar
19.Keel, S., Intersection theory of moduli space of stable n-pointed curves of genus zero, Trans. Amer. Math. Soc. 330 (1992), 545–574.Google Scholar
20.Keel, S. and Tevelev, J., Geometry of Chow quotients of Grassmannians, Duke Math. J. 134(2) (2006), 259–311.Google Scholar
21.Kim, B. and Sato, F., A generalization of Fulton-MacPherson configuration spaces, Selecta Math. (N.S.) 15(3) (2009), 435–443.Google Scholar
22.Kirwan, F., Quotients by non-reductive algebraic group actions, In Moduli spaces and vector bundles, London Mathematical Society Lecture Note Series, Volume 359, pp. 311–366 (Cambridge University Press, Cambridge, 2009).Google Scholar
23.Knudsen, F. F., The projectivity of the moduli space of stable curves. II. The stacks M g, n, Math. Scand. 52(2) (1983), 161–199.Google Scholar
24.Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Volume 32 (Springer, Berlin, 1996).Google Scholar
25.Lafforgue, L., Chirurgie des grassmanniennes, CRM Monograph Series, Volume 19 (American Mathematical Society, Providence, RI, 2003).Google Scholar
26.Manin, Y. I. and Marcolli, M., Big Bang, blowup, and modular curves: algebraic geometry in cosmology, SIGMA Symmetry Integrability Geom. Methods Appl. 10 (2014), 073.Google Scholar
27.Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory, 3rd edition, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], Volume 34 (Springer, Berlin, 1994).Google Scholar
28.Pixton, A., A nonboundary nef divisor on , Geom. Topol. 17(3) (2013), 1317–1324.Google Scholar
29.Westerland, C., Operads of moduli spaces of points in ℂd, Proc. Amer. Math. Soc. 141(9) (2013), 3029–3035.Google Scholar