Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T00:24:28.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank 3 rigid representations of projective fundamental groups

Part of: Birational geometry (Co)homology theory Families, fibrations

Published online by Cambridge University Press:  30 May 2018

Adrian Langer  and
Carlos Simpson
Adrian Langer
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097 Warszawa, Poland email [email protected]
Carlos Simpson
Affiliation:
Laboratoire J. A. Dieudonné, CNRS UMR 7351, Université Côte d’Azur, 06108 Nice, Cedex 2, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 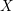$X$ be a smooth complex projective variety with basepoint $x$ . We prove that every rigid integral irreducible representation 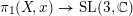$\unicode[STIX]{x1D70B}_{1}(X\!,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$ is of geometric origin, i.e., it comes from some family of smooth projective varieties. This partially generalizes an earlier result by Corlette and the second author in the rank 2 case and answers one of their questions.

Keywords

fundamental groupcomplex varietiesrigid representationcomplex variation of Hodge structure

MSC classification

Primary: 14F35: Homotopy theory; fundamental groups
Secondary: 14D06: Fibrations, degenerations 14D07: Variation of Hodge structures 14E20: Coverings
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 7 , July 2018 , pp. 1534 - 1570
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bass, H., Groups of integral representation type , Pacific J. Math. 86 (1980), 15–51.Google Scholar
Beauville, A., Annulation du H 1 pour les fibrés en droites plats , in Complex algebraic varieties (Bayreuth, 1990), Lecture Notes in Mathematics, vol. 1507 (Springer, Berlin, 1992), 1–15.CrossRefGoogle Scholar
Behrend, K. and Noohi, B., Uniformization of Deligne–Mumford curves , J. Reine Angew. Math. 599 (2006), 111–153.Google Scholar
Bhatt, B., Annihilating the cohomology of group schemes , Algebra Number Theory 6 (2012), 1561–1577.Google Scholar
Bogomolov, F. A., Holomorphic tensors and vector bundles on projective manifolds , Izv. Akad. Nauk SSSR Ser. Mat. 42 (1978), 1227–1287; 1439.Google Scholar
Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).Google Scholar
Catanese, F. and Dettweiler, M., Answer to a question by Fujita on variation of Hodge structures , in Higher Dimensional Algebraic Geometry: In Honor of Professor Yujiro Kawamata’s 60th Birthday, Advanced Studies in Pure Mathematics, vol. 74 (Kinokuniya, Tokyo, 2017), 73–102.Google Scholar
Corlette, K. and Simpson, C., On the classification of rank-two representations of quasiprojective fundamental groups , Compos. Math. 144 (2008), 1271–1331.CrossRefGoogle Scholar
Cousin, G., Projective representations of fundamental groups of quasiprojective varieties: a realization and a lifting result , C. R. Math. Acad. Sci. Paris 353 (2015), 155–159.Google Scholar
Debarre, O., Complex tori and abelian varieties, SMF/AMS Texts and Monographs, vol. 11 (American Mathematical Society, Providence, RI; Société Mathématique de France, Paris, 2005).Google Scholar
Deligne, P., Travaux de Shimura , in Séminaire N. Bourbaki (1970/71), exp. 389, Lecture Notes in Mathematics, vol. 244 (Springer, Berlin, 1971), 123–165.Google Scholar
de Jong, A. J., A conjecture on arithmetic fundamental groups , Israel J. Math. 121 (2001), 61–84.Google Scholar
Esnault, H. and Groechenig, M., Cohomologically rigid connections and integrality, Selecta Math. (N.S.), to appear. Preprint (2017), arXiv:1711.06436.Google Scholar
Esnault, H. and Viehweg, E., Lectures on vanishing theorems, DMV Seminar, vol. 20 (Birkhäuser, Basel, 1992).CrossRefGoogle Scholar
Fujita, T., The sheaf of relative canonical forms of a Kähler fiber space over a curve , Proc. Japan Acad. Ser. A 54 (1978), 183–184.CrossRefGoogle Scholar
Green, M. and Lazarsfeld, R., Higher obstructions to deforming cohomology groups of line bundles , J. Amer. Math. Soc. 4 (1991), 87–103.Google Scholar
Gromov, M. and Schoen, R., Harmonic maps into singular spaces and p-adic superrigidity for lattices in groups of rank one , Publ. Math. Inst. Hautes Études Sci. 76 (1992), 165–246.Google Scholar
Hamm, H. A. and Lê, D. T., Lefschetz theorems on quasiprojective varieties , Bull. Soc. Math. France 113 (1985), 123–142.CrossRefGoogle Scholar
Iyer, J. N. N. and Simpson, C. T., A relation between the parabolic Chern characters of the de Rham bundles , Math. Ann. 338 (2007), 347–383.CrossRefGoogle Scholar
Katz, N. M., Rigid local systems, Annals of Mathematics Studies, vol. 139 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Katz, N. M., L-functions and monodromy: four lectures on Weil II , Adv. Math. 160 (2001), 81–132.Google Scholar
Klingler, B., Sur la rigidité de certains groupes fondamentaux, l’arithméticité des réseaux hyperboliques complexes, et les “faux plans projectifs” , Invent. Math. 153 (2003), 105–143.Google Scholar
Klingler, B., Symmetric differentials, Kähler groups and ball quotients , Invent. Math. 192 (2013), 257–286.Google Scholar
Langer, A., A note on Bogomolov’s instability and Higgs sheaves , in Algebraic geometry: a volume in memory of Paolo Francia, eds Beltrametti, M. et al. (Walter de Gruyter, Berlin, 2002), 237–256.Google Scholar
Langer, A., Bogomolov’s inequality for Higgs sheaves in positive characteristic , Invent. Math. 199 (2015), 889–920.CrossRefGoogle Scholar
Langer, A., The Bogomolov–Miyaoka–Yau inequality for logarithmic surfaces in positive characteristic , Duke Math. J. 165 (2016), 2737–2769.Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 48 (Springer, Berlin, 2004).Google Scholar
Mochizuki, T., Kobayashi–Hitchin correspondence for tame harmonic bundles and an application , Astérisque 309 (2006).Google Scholar
Mochizuki, T., Kobayashi-Hitchin correspondence for tame harmonic bundles. II , Geom. Topol. 13 (2009), 359–455.CrossRefGoogle Scholar
Nori, M. V., Zariski’s conjecture and related problems , Ann. Sci. Éc. Norm. Supér. (4) 16 (1983), 305–344.CrossRefGoogle Scholar
Simpson, C. T., Higgs bundles and local systems , Publ. Math. Inst. Hautes Études Sci. 75 (1992), 5–95.Google Scholar
Simpson, C. T., Lefschetz theorems for the integral leaves of a holomorphic one-form , Compos. Math. 87 (1993), 99–113.Google Scholar
Simpson, C. T., Subspaces of moduli spaces of rank one local systems , Ann. Sci. Éc. Norm. Supér. (4) 26 (1993), 361–401.CrossRefGoogle Scholar
Totaro, B., The topology of smooth divisors and the arithmetic of abelian varieties , Michigan Math. J. 48 (2000), 611–624.CrossRefGoogle Scholar
Totaro, B., Euler and algebraic geometry , Bull. Amer. Math. Soc. 44 (2007), 541–559.CrossRefGoogle Scholar
Weil, A., Discrete subgroups of Lie groups, II , Annals of Math. 75 (1962), 97–123.Google Scholar
Xiao, G., 𝜋1 of elliptic and hyperelliptic surfaces , Internat. J. Math. 2 (1991), 599–615.CrossRefGoogle Scholar
Zuo, K., Representations of fundamental groups of algebraic varieties, Lecture Notes in Mathematics, vol. 1708 (Springer, Berlin, 1999).Google Scholar