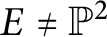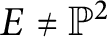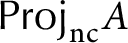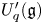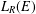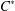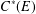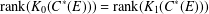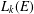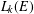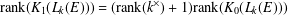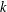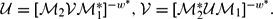41 results
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The generalized auslander–reiten duality on a module category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 167-181
-
- Article
- Export citation
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simply laced root systems arising from quantum affine algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 168-210
- Print publication:
- January 2022
-
- Article
- Export citation
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
On dualizability of braided tensor categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 435-483
- Print publication:
- March 2021
-
- Article
- Export citation
Representability and autoequivalence groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 657-668
- Print publication:
- November 2021
-
- Article
- Export citation
GORENSTEIN SILTING COMPLEXES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 January 2021, pp. 122-135
- Print publication:
- January 2022
-
- Article
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- Export citation
REPETITIVE EQUIVALENCES AND TILTING THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 97-136
- Print publication:
- September 2021
-
- Article
- Export citation
ALGEBRAIC CUNTZ–KRIEGER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 23 September 2019, pp. 93-111
- Print publication:
- August 2020
-
- Article
- Export citation
INVARIANCE OF THE GERSTENHABER ALGEBRA STRUCTURE ON TATE-HOCHSCHILD COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 15 July 2019, pp. 893-928
- Print publication:
- May 2021
-
- Article
- Export citation
Integrable Derivations and Stable Equivalences of Morita Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 343-362
-
- Article
- Export citation
LATTICE STRUCTURE OF TORSION CLASSES FOR HEREDITARY ARTIN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 05 June 2017, pp. 89-100
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
Pure Injective and Absolutely Pure Sheaves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 623-640
-
- Article
- Export citation
STABLE PROPERTIES OF HYPERRELEXIVITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 205-218
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation