Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-23T04:23:35.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Laurent family of simple modules over quiver Hecke algebras

Part of: Lie algebras and Lie superalgebras Modules, bimodules and ideals Groups and algebras in quantum theory Arithmetic rings and other special rings

Published online by Cambridge University Press:  11 September 2024

Masaki Kashiwara Open the ORCID record for Masaki Kashiwara [Opens in a new window] ,
Myungho Kim Open the ORCID record for Myungho Kim [Opens in a new window] ,
Se-jin Oh Open the ORCID record for Se-jin Oh [Opens in a new window]  and
Euiyong Park Open the ORCID record for Euiyong Park [Opens in a new window]
Masaki Kashiwara
Affiliation:
Kyoto University Institute for Advanced Study, Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan and Korea Institute for Advanced Study, Seoul 02455, South Korea masaki@kurims.kyoto-u.ac.jp
Myungho Kim
Affiliation:
Department of Mathematics, Kyung Hee University, Seoul 02447, South Korea mkim@khu.ac.kr
Se-jin Oh
Affiliation:
Department of Mathematics, Sungkyunkwan University, Suwon 16419, South Korea sejin092@gmail.com
Euiyong Park
Affiliation:
Department of Mathematics, University of Seoul, Seoul 02504, South Korea epark@uos.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notions of quasi-Laurent and Laurent families of simple modules over quiver Hecke algebras of arbitrary symmetrizable types. We prove that such a family plays a similar role of a cluster in quantum cluster algebra theory and exhibits a quantum Laurent positivity phenomenon similar to the basis of the quantum unipotent coordinate ring 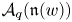$\mathcal {A}_q(\mathfrak {n}(w))$, coming from the categorification. Then we show that the families of simple modules categorifying Geiß–Leclerc–Schröer (GLS) clusters are Laurent families by using the Poincaré–Birkhoff–Witt (PBW) decomposition vector of a simple module 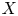$X$ and categorical interpretation of (co)degree of 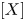$[X]$. As applications of such 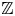$\mathbb {Z}\mspace {1mu}$-vectors, we define several skew-symmetric pairings on arbitrary pairs of simple modules, and investigate the relationships among the pairings and $\Lambda$-invariants of 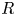$R$-matrices in the quiver Hecke algebra theory.

Keywords

Laurent familyquantum Laurent positivityquantum cluster algebrag-vectorR-matrix

MSC classification

Primary: 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 13F60: Cluster algebras 81R50: Quantum groups and related algebraic methods 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 8 , August 2024 , pp. 1916 - 1940
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berenstein, A. and Zelevinsky, A., Quantum cluster algebras, Adv. Math. 195 (2005), 405–455; MR 2146350.CrossRefGoogle Scholar
Davison, B., Positivity for quantum cluster algebras, Ann. of Math. (2) 187 (2018), 157–219.CrossRefGoogle Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: applications to cluster algebras, J. Amer. Math. Soc. 23 (2010), 749–790; MR 2629987.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations, J. Amer. Math. Soc. 15 (2002), 497–529; MR 1887642.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. IV. Coefficients, Compos. Math. 143 (2007), 112–164; MR 2295199.CrossRefGoogle Scholar
Fujita, R. and Oh, S.-j., Q-data and representation theory of untwisted quantum affine algebras, Comm. Math. Phys. 384 (2021), 1351–1407; MR 4259388.CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J., Cluster structures on quantum coordinate rings, Selecta Math. (N.S.) 19 (2013), 337–397; MR 3090232.CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J., Factorial cluster algebras, Doc. Math. 18 (2013), 249–274.CrossRefGoogle Scholar
Goodearl, K. R. and Yakimov, M. T., Quantum cluster algebra structures on quantum nilpotent algebras, Mem. Amer. Math. Soc. 247 (2017); MR 3633289.Google Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., Canonical bases for cluster algebras, J. Amer. Math. Soc. 31 (2018), 497–608; MR 3758151.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., Cluster algebras and quantum affine algebras, Duke Math. J. 154 (2010), 265–341; MR 2682185.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., Quantum Grothendieck rings and derived Hall algebras, J. Reine Angew. Math. 701 (2015), 77–126; MR 3331727.CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M. and Kim, M., Symmetric quiver Hecke algebras and $R$-matrices of quantum affine algebras, Invent. Math. 211 (2018), 591–685.CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-j., Simplicity of heads and socles of tensor products, Compos. Math. 151 (2015), 377–396.CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-j., Monoidal categorification of cluster algebras, J. Amer. Math. Soc. 31 (2018), 349–426; MR 3758148.CrossRefGoogle Scholar
Kashiwara, M. and Kim, M., Laurent phenomenon and simple modules of quiver Hecke algebras, Compos. Math. 155 (2019), 2263–2295; MR 4016058.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-j. and Park, E., Monoidal categories associated with strata of flag manifolds, Adv. Math. 328 (2018), 959–1009.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-j. and Park, E., Localizations for quiver Hecke algebras, Pure Appl. Math. Q. 17 (2021), 1465–1548.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-j. and Park, E., Localizations for quiver hecke algebras II, Proc. Lond. Math. Soc. 127 (2023), 1134–1184.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-j. and Park, E., Affinizations, $R$-matrices and reflection functors, Adv. Math. 443 (2024), 109598.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-j. and Park, E., Monoidal categorification and quantum affine algebras II, Invent. Math. 236 (2024), 837–924.CrossRefGoogle Scholar
Kashiwara, M. and Oh, S.-j., The $(q, t)$-Cartan matrix specialized at $q= 1$ and its applications, Math. Z. 303 (2023), article 42.CrossRefGoogle Scholar
Kashiwara, M. and Park, E., Affinizations and $R$-matrices for quiver Hecke algebras, J. Eur. Math. Soc. (JEMS) 20 (2018), 1161–1193.CrossRefGoogle Scholar
Khovanov, M. and Lauda, A. D., A diagrammatic approach to categorification of quantum groups $I$, Represent. Theory 13 (2009), 309–347.CrossRefGoogle Scholar
Khovanov, M. and Lauda, A. D., A diagrammatic approach to categorification of quantum groups $II$, Trans. Amer. Math. Soc. 363 (2011), 2685–2700.CrossRefGoogle Scholar
Kimura, Y., Quantum unipotent subgroup and dual canonical basis, Kyoto J. Math. 52 (2012), 277–331; MR 2914878.CrossRefGoogle Scholar
Kimura, Y. and Oya, H., Twist automorphisms on quantum unipotent cells and dual canonical bases, Int. Math. Res. Not. IMRN 2021 (2021), 6772–6847.CrossRefGoogle Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras, Ann. of Math. (2) 182 (2015), 73–125.CrossRefGoogle Scholar
McNamara, P. J., Finite dimensional representations of Khovanov–Lauda–Rouquier algebras $I$: finite type, J. Reine Angew. Math. 707 (2015), 103–124.CrossRefGoogle Scholar
Qin, F., Dual canonical bases and quantum cluster algebras, Preprint (2020), arXiv:2003.13674.Google Scholar
Qin, F., Triangular bases in quantum cluster algebras and monoidal categorification conjectures, Duke Math. J. 166 (2017), 2337–2442; MR 3694569.CrossRefGoogle Scholar
Rouquier, R., 2-Kac-Moody algebras, Preprint (2008), arXiv:0812.5023.Google Scholar
Tingley, P. and Webster, B., Mirković–Vilonen polytopes and Khovanov–Lauda–Rouquier algebras, Compos. Math. 152 (2016), 1648–1696.CrossRefGoogle Scholar
Tran, T., $F$-polynomials in quantum cluster algebras, Algebr. Represent. Theory 14 (2011), 1025–1061; MR 2844755.CrossRefGoogle Scholar