Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T06:22:02.747Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC CUNTZ–KRIEGER ALGEBRAS

Part of: Rings and algebras with additional structure Modules, bimodules and ideals Homological methods

Published online by Cambridge University Press:  23 September 2019

ALIREZA NASR-ISFAHANI
ALIREZA NASR-ISFAHANI*
Affiliation:
Department of Mathematics, University of Isfahan, PO Box 81746-73441, Isfahan, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a directed graph 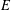$E$ is a finite graph with no sinks if and only if, for each commutative unital ring 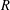$R$, the Leavitt path algebra 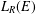$L_{R}(E)$ is isomorphic to an algebraic Cuntz–Krieger algebra if and only if the 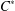$C^{\ast }$-algebra 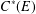$C^{\ast }(E)$ is unital and 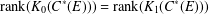$\text{rank}(K_{0}(C^{\ast }(E)))=\text{rank}(K_{1}(C^{\ast }(E)))$. Let 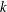$k$ be a field and 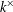$k^{\times }$ be the group of units of 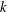$k$. 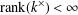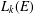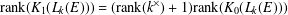When $\text{rank}(k^{\times })<\infty$, we show that the Leavitt path algebra $L_{k}(E)$ is isomorphic to an algebraic Cuntz–Krieger algebra if and only if $L_{k}(E)$ is unital and $\text{rank}(K_{1}(L_{k}(E)))=(\text{rank}(k^{\times })+1)\text{rank}(K_{0}(L_{k}(E)))$. We also show that any unital $k$-algebra which is Morita equivalent or stably isomorphic to an algebraic Cuntz–Krieger algebra, is isomorphic to an algebraic Cuntz–Krieger algebra. As a consequence, corners of algebraic Cuntz–Krieger algebras are algebraic Cuntz–Krieger algebras.

Keywords

Leavitt path algebraCuntz–Krieger algebrastably isomorphicMorita equivalence

MSC classification

Primary: 16W99: None of the above, but in this section
Secondary: 16E20: Grothendieck groups, $K$-theory, etc. 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 1 , August 2020 , pp. 93 - 111
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was in part supported by a grant from IPM (no. 95170419).

References

Abrams, G. and Aranda Pino, G., ‘The Leavitt path algebra of a graph’, J. Algebra 293(2) (2005), 319–334.Google Scholar
Abrams, G., Louly, A., Pardo, E. and Smith, C., ‘Flow invariants in the classification of Leavitt path algebras’, J. Algebra 333 (2011), 202–231.Google Scholar
Abrams, G. and Tomforde, M., ‘Isomorphism and Morita equivalence of graph algebras’, Trans. Amer. Math. Soc. 363 (2011), 3733–3767.Google Scholar
Ara, P., Brustenga, M. and Cortinas, G., ‘K-theory of Leavitt path algebras’, Münster J. Math. 2 (2009), 5–33.Google Scholar
Ara, P., Gonzalez-Barroso, M. A., Goodearl, K. R. and Pardo, E., ‘Fractional skew monoid rings’, J. Algebra 278 (2004), 104–126.Google Scholar
Ara, P., Moreno, M. A. and Pardo, E., ‘Nonstable K-theory for graph algebras’, Algebr. Represent. Theory 10 (2007), 157–178.Google Scholar
Aranda Pino, G., Martín Barquero, D., Martín González, C. and Siles Molina, M., ‘Socle theory for Leavitt path algebras of arbitrary graphs’, Rev. Mat. Iberoam. 26(2) (2010), 611–638.Google Scholar
Aranda Pino, G., Pardo, E. and Siles Molina, M., ‘Exchange Leavitt path algebras and stable rank’, J. Algebra 305(2) (2006), 912–936.Google Scholar
Arklint, A. E. and Ruiz, E., ‘Corners of Cuntz–Krieger algebras’, Trans. Amer. Math. Soc. 367 (2015), 7595–7612.Google Scholar
Crisp, T., ‘Corners of graph algebras’, J. Operator Theory 60(2) (2008), 253–271.Google Scholar
Cuntz, J. and Krieger, W., ‘A class of C ∗ -algebras and topological Markov chains’, Invent. Math. 56(3) (1980), 251–268.Google Scholar
Gabe, J., Ruiz, E., Tomforde, M. and Whalen, T., ‘K-theory for Leavitt path algebras: computation and classification’, J. Algebra 433 (2015), 35–72.Google Scholar
Gil Canto, C. and Nasr-Isfahani, A., ‘The commutative core of a Leavitt path algebra’, J. Algebra 511 (2018), 227–248.Google Scholar
Hazrat, R., ‘The dynamics of Leavitt path algebras’, J. Algebra 384 (2013), 242–266.Google Scholar
Hazrat, R., ‘The graded structure of Leavitt path algebras’, Israel J. Math. 195 (2013), 833–895.Google Scholar
Leavitt, W. G., ‘Modules without invariant basis number’, Proc. Amer. Math. Soc. 8 (1957), 322–328.Google Scholar
Nam, T. G. and Phuc, N. T., ‘A criterion for Leavitt path algebras having invariant basis number’, Preprint, 2016, arXiv:1606.04607.Google Scholar
Nasr-Isfahani, A. R., ‘Singular equivalence of finite dimensional algebras with radical square zero’, J. Pure Appl. Algebra 220 (2016), 3948–3965.Google Scholar
Raeburn, I., Graph Algebras, CBMS Regional Conference Series in Mathematics, 103 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Ruiz, E. and Tomforde, M., ‘Classification of unital simple Leavitt path algebras of infinite graphs’, J. Algebra 384 (2013), 45–83.Google Scholar
Tomforde, M., ‘Leavitt path algebras with coefficients in a commutative ring’, J. Pure Appl. Algebra 215 (2011), 471–484.Google Scholar
Watatani, Y., ‘Graph theory for C ∗ -algebras’, in: Operator Algebras and Applications, Part I (Kingston, ON, 1980), Proceedings of Symposia in Pure Mathematics, 38 (American Mathematical Society, Providence, RI, 1982), 195–197.Google Scholar