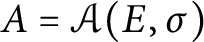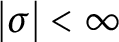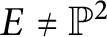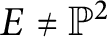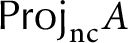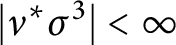1 Introduction
A quantum polynomial algebra is a noncommutative analogue of a commutative polynomial algebra, and a quantum projective space is the noncommutative projective scheme associated to a quantum polynomial algebra, so they are the most basic objects to study in noncommutative algebraic geometry. In fact, the starting point of the subject noncommutative algebraic geometry is the paper [Reference Artin and Zhang3] by Artin, Tate, and Van den Bergh, showing that there exists a nice correspondence between three-dimensional quantum polynomial algebras A and geometric pairs
![]() $(E, \sigma )$
where
$(E, \sigma )$
where
![]() $E=\mathbb P^{2}$
or a cubic divisor in
$E=\mathbb P^{2}$
or a cubic divisor in
![]() $\mathbb P^{2}$
, and
$\mathbb P^{2}$
, and
![]() $\sigma \in \text {Aut} E$
, so the classification of three-dimensional quantum polynomial algebras reduces to the classification of “regular” geometric pairs. Write
$\sigma \in \text {Aut} E$
, so the classification of three-dimensional quantum polynomial algebras reduces to the classification of “regular” geometric pairs. Write
![]() $A=\mathcal A(E, \sigma )$
for a three-dimensional quantum polynomial algebra corresponding to the geometric pair
$A=\mathcal A(E, \sigma )$
for a three-dimensional quantum polynomial algebra corresponding to the geometric pair
![]() $(E, \sigma )$
. The geometric properties of the geometric pair
$(E, \sigma )$
. The geometric properties of the geometric pair
![]() $(E, \sigma )$
provide some algebraic properties of
$(E, \sigma )$
provide some algebraic properties of
![]() $A=\mathcal A(E, \sigma )$
. One of the most striking results of such is in the companion paper [Reference Artin, Tate and Van den Bergh4].
$A=\mathcal A(E, \sigma )$
. One of the most striking results of such is in the companion paper [Reference Artin, Tate and Van den Bergh4].
Theorem 1.1 [Reference Artin, Tate and Van den Bergh4, Theorem 7.1]
Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. Then
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. Then
![]() $|\sigma |<\infty $
if and only if A is finite over its center.
$|\sigma |<\infty $
if and only if A is finite over its center.
Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. To prove the above theorem, fat points of the quantum projective plane
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. To prove the above theorem, fat points of the quantum projective plane
![]() ${\sf Proj}_{\text {nc}} A$
play an essential role. By Artin [Reference Artin2], if A is finite over its center and
${\sf Proj}_{\text {nc}} A$
play an essential role. By Artin [Reference Artin2], if A is finite over its center and
![]() $E\neq \mathbb {P}^{2}$
, then
$E\neq \mathbb {P}^{2}$
, then
![]() ${\sf Proj}_{\text {nc}} A$
has a fat point; however, the converse is not true. To check the existence of a fat point, there is a more important notion than
${\sf Proj}_{\text {nc}} A$
has a fat point; however, the converse is not true. To check the existence of a fat point, there is a more important notion than
![]() $|\sigma |$
, namely,
$|\sigma |$
, namely,
In fact,
![]() ${\sf Proj}_{\text {nc}} A$
has a fat point if and only if
${\sf Proj}_{\text {nc}} A$
has a fat point if and only if
![]() $1<\|\sigma \|<\infty $
by [Reference Artin2].
$1<\|\sigma \|<\infty $
by [Reference Artin2].
In [Reference Mori13], the notion that
![]() ${\sf Proj}_{\text {nc}} A$
is finite over its center was introduced, and the following result was proved.
${\sf Proj}_{\text {nc}} A$
is finite over its center was introduced, and the following result was proved.
Theorem 1.2 [Reference Mori13, Theorem 4.17]
Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra such that
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra such that
![]() $E\subset \mathbb P^{2}$
is a triangle. Then
$E\subset \mathbb P^{2}$
is a triangle. Then
![]() $\|\sigma \|<\infty $
if and only if
$\|\sigma \|<\infty $
if and only if
![]() ${\sf Proj}_{\text {nc}} A$
is finite over its center.
${\sf Proj}_{\text {nc}} A$
is finite over its center.
The purpose of this paper is to extend the above theorem to all three-dimensional quantum polynomial algebras. In fact, the following is our main result.
Theorem 1.3 (Theorem 3.6 and Corollary 4.1)
Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra such that
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra such that
![]() $E\neq \mathbb P^{2}$
, and
$E\neq \mathbb P^{2}$
, and
![]() $\nu \in \text {Aut} A$
the Nakayama automorphism of A. Then the following are equivalent:
$\nu \in \text {Aut} A$
the Nakayama automorphism of A. Then the following are equivalent:
-
(1)
 $|\nu ^{*}\sigma ^{3}|<\infty $
.
$|\nu ^{*}\sigma ^{3}|<\infty $
. -
(2)
 $\|\sigma \|<\infty $
.
$\|\sigma \|<\infty $
. -
(3)
 ${\sf Proj}_{\text {nc}} A$
is finite over its center.
${\sf Proj}_{\text {nc}} A$
is finite over its center. -
(4)
 ${\sf Proj}_{\text {nc}} A$
has a fat point.
${\sf Proj}_{\text {nc}} A$
has a fat point.
Note that if
![]() $E=\mathbb P^{2}$
, then
$E=\mathbb P^{2}$
, then
![]() $||\sigma ||=1$
, but
$||\sigma ||=1$
, but
![]() $\text {Proj}_{\text {nc}}A$
has no fat point (see Lemma 2.14).
$\text {Proj}_{\text {nc}}A$
has no fat point (see Lemma 2.14).
As a biproduct, we have the following corollary.
Corollary 1.4 Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. If the second Hessian of E is zero, then A is never finite over its center.
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. If the second Hessian of E is zero, then A is never finite over its center.
These results are important to study representation theory of the Beilinson algebra
![]() $\nabla A$
, which is a typical example of a
$\nabla A$
, which is a typical example of a
![]() $2$
-representation infinite algebra defined in [Reference Herschend, Iyama and Oppermann6]. This was the original motivation of the paper [Reference Mori13].
$2$
-representation infinite algebra defined in [Reference Herschend, Iyama and Oppermann6]. This was the original motivation of the paper [Reference Mori13].
2 Preliminaries
Throughout this paper, we fix an algebraically closed field k of characteristic
![]() $0$
. All algebras and (noncommutative) schemes are defined over k. We further assume that all (graded) algebras are finitely generated (in degree
$0$
. All algebras and (noncommutative) schemes are defined over k. We further assume that all (graded) algebras are finitely generated (in degree
![]() $1$
) over k, that is, algebras of the form
$1$
) over k, that is, algebras of the form
![]() $k\langle x_{1}, \dots , x_{n}\rangle /I$
for some (homogeneous) ideal
$k\langle x_{1}, \dots , x_{n}\rangle /I$
for some (homogeneous) ideal
![]() $I\lhd k\langle x_{1}, \dots , x_{n}\rangle $
(where
$I\lhd k\langle x_{1}, \dots , x_{n}\rangle $
(where
![]() $\deg x_{i}=1$
for every
$\deg x_{i}=1$
for every
![]() $i=1, \dots , n$
).
$i=1, \dots , n$
).
2.1 Geometric quantum polynomial algebras
In this subsection, we define geometric algebras and quantum polynomial algebras.
Definition 2.1 [Reference Mori12, Definition 4.3]
A geometric pair
![]() $(E,\sigma )$
consists of a projective scheme
$(E,\sigma )$
consists of a projective scheme
![]() $E \subset \mathbb P^{n-1}$
and
$E \subset \mathbb P^{n-1}$
and
![]() $\sigma \in \text {Aut}_{k}\,E$
. For a quadratic algebra
$\sigma \in \text {Aut}_{k}\,E$
. For a quadratic algebra
![]() $A=k\langle x_{1}, \dots , x_{n}\rangle /I$
where
$A=k\langle x_{1}, \dots , x_{n}\rangle /I$
where
![]() $I\lhd k\langle x_{1}, \dots , x_{n}\rangle $
is a homogeneous ideal generated by elements of degree
$I\lhd k\langle x_{1}, \dots , x_{n}\rangle $
is a homogeneous ideal generated by elements of degree
![]() $2$
, we define
$2$
, we define
-
(1) We say that A satisfies (G
 $1$
) if there exists a geometric pair
$1$
) if there exists a geometric pair
 $(E,\sigma )$
such that In this case, we write
$(E,\sigma )$
such that In this case, we write $$ \begin{align*} \mathcal{V}(I_{2})=\{ (p,\sigma(p)) \in \mathbb{P}^{n-1}\times \mathbb P^{n-1} \,|\,p \in E \}. \end{align*} $$
$$ \begin{align*} \mathcal{V}(I_{2})=\{ (p,\sigma(p)) \in \mathbb{P}^{n-1}\times \mathbb P^{n-1} \,|\,p \in E \}. \end{align*} $$
 $\mathcal {P}(A)=(E,\sigma )$
, and call E the point scheme of A.
$\mathcal {P}(A)=(E,\sigma )$
, and call E the point scheme of A.
-
(2) We say that A satisfies (G
 $2$
) if there exists a geometric pair
$2$
) if there exists a geometric pair
 $(E,\sigma )$
such that In this case, we write
$(E,\sigma )$
such that In this case, we write $$ \begin{align*} I_{2}=\{ f \in k\langle x_{1}, \dots, x_{n}\rangle_{2} \,|\,f(p,\sigma(p))=0\,\,\text{for any } p \in E \}. \end{align*} $$
$$ \begin{align*} I_{2}=\{ f \in k\langle x_{1}, \dots, x_{n}\rangle_{2} \,|\,f(p,\sigma(p))=0\,\,\text{for any } p \in E \}. \end{align*} $$
 $A=\mathcal {A}(E,\sigma )$
.
$A=\mathcal {A}(E,\sigma )$
.
-
(3) A quadratic algebra A is called geometric if A satisfies both (G1) and (G2) with
 $A=\mathcal {A}(\mathcal {P}(A))$
.
$A=\mathcal {A}(\mathcal {P}(A))$
.
Definition 2.2 A right Noetherian graded algebra A is called a d-dimensional quantum polynomial algebra if
-
(1)
 $\operatorname {gldim} A=d$
,
$\operatorname {gldim} A=d$
, -
(2)
 $\text {Ext}^{i}_{A}(k, A)\cong \begin {cases} k & \text { if } i=d, \\ 0 & \text { if } i\neq d, \end {cases}$
and
$\text {Ext}^{i}_{A}(k, A)\cong \begin {cases} k & \text { if } i=d, \\ 0 & \text { if } i\neq d, \end {cases}$
and -
(3)
 $H_{A}(t):=\sum _{i=0}^{\infty }(\dim _{k}A_{i})t^{i}=(1-t)^{-d}$
.
$H_{A}(t):=\sum _{i=0}^{\infty }(\dim _{k}A_{i})t^{i}=(1-t)^{-d}$
.
Note that a three-dimensional quantum polynomial algebra is exactly the same as a three-dimensional quadratic AS-regular algebra, so we have the following result.
Theorem 2.1 [Reference Artin and Zhang3]
Every three-dimensional quantum polynomial algebra is a geometric algebra where the point scheme is either
![]() $\mathbb P^{2}$
or a cubic divisor in
$\mathbb P^{2}$
or a cubic divisor in
![]() $\mathbb P^{2}$
.
$\mathbb P^{2}$
.
Remark 2.2 There exists a four-dimensional quantum polynomial algebra which is not a geometric algebra; however, as far as we know, there exists no example of a quantum polynomial algebra which does not satisfy (G1).
We define the type of a three-dimensional quantum polynomial algebra
![]() $A=\mathcal A(E, \sigma )$
in terms of the point scheme
$A=\mathcal A(E, \sigma )$
in terms of the point scheme
![]() $E\subset \mathbb P^{2}$
.
$E\subset \mathbb P^{2}$
.
-
Type P E is
 $\mathbb {P}^{2}$
.
$\mathbb {P}^{2}$
. -
Type S E is a triangle.
-
Type S’ E is a union of a line and a conic meeting at two points.
-
Type T E is a union of three lines meeting at one point.
-
Type T’ E is a union of a line and a conic meeting at one point.
-
Type NC E is a nodal cubic curve.
-
Type CC E is a cuspidal cubic curve.
-
Type TL E is a triple line.
-
Type WL E is a union of a double line and a line.
-
Type EC E is an elliptic curve.
2.2 Quantum projective spaces finite over their centers
Definition 2.3
A noncommutative scheme (over k) is a pair
![]() $X=({\sf mod} X, \mathcal O_{X})$
consisting of a k-linear abelian category
$X=({\sf mod} X, \mathcal O_{X})$
consisting of a k-linear abelian category
![]() ${\sf mod} X$
and an object
${\sf mod} X$
and an object
![]() $\mathcal O_{X}\in {\sf mod} X$
. We say that two noncommutative schemes
$\mathcal O_{X}\in {\sf mod} X$
. We say that two noncommutative schemes
![]() $X=(\textsf{mod} X, \mathcal O_{X})$
and
$X=(\textsf{mod} X, \mathcal O_{X})$
and
![]() $Y=(\textsf{mod} Y, \mathcal O_{Y})$
are isomorphic, denoted by
$Y=(\textsf{mod} Y, \mathcal O_{Y})$
are isomorphic, denoted by
![]() $X\cong Y$
, if there exists an equivalence functor
$X\cong Y$
, if there exists an equivalence functor
![]() $F:{\sf mod} X\to {\sf mod} Y$
such that
$F:{\sf mod} X\to {\sf mod} Y$
such that
![]() $F(\mathcal O_{X})\cong \mathcal O_{Y}$
.
$F(\mathcal O_{X})\cong \mathcal O_{Y}$
.
If X is a commutative Noetherian scheme, then we view X as a noncommutative scheme by
![]() $({\sf mod} X, \mathcal O_{X})$
where
$({\sf mod} X, \mathcal O_{X})$
where
![]() ${\sf mod} X$
is the category of coherent sheaves on X and
${\sf mod} X$
is the category of coherent sheaves on X and
![]() $\mathcal O_{X}$
is the structure sheaf on X.
$\mathcal O_{X}$
is the structure sheaf on X.
Noncommutative affine and projective schemes are defined in [Reference Artin, Tate and Van den Bergh5].
Definition 2.4 If R is a right Noetherian algebra, then we define the noncommutative affine scheme associated to R by
![]() ${\sf Spec}_{\text {nc}} R=({\sf mod} R, R)$
where
${\sf Spec}_{\text {nc}} R=({\sf mod} R, R)$
where
![]() ${\sf mod} R$
is the category of finitely generated right R-modules and
${\sf mod} R$
is the category of finitely generated right R-modules and
![]() $R\in {\sf mod} R$
is the regular right module.
$R\in {\sf mod} R$
is the regular right module.
Note that if R is commutative, then
![]() ${\sf Spec}_{\text {nc}} R\cong {\sf Spec} R$
.
${\sf Spec}_{\text {nc}} R\cong {\sf Spec} R$
.
Definition 2.5 If A is a right Noetherian graded algebra,
![]() ${\sf grmod} A$
is the category of finitely generated graded right A-modules, and
${\sf grmod} A$
is the category of finitely generated graded right A-modules, and
![]() ${\sf tors} A$
is the full subcategory of
${\sf tors} A$
is the full subcategory of
![]() ${\sf grmod} A$
consisting of finite-dimensional modules over k, then we define the noncommutative projective scheme associated to A by
${\sf grmod} A$
consisting of finite-dimensional modules over k, then we define the noncommutative projective scheme associated to A by
![]() ${\sf Proj}_{\text {nc}} A=({\sf tails} A, \pi A)$
where
${\sf Proj}_{\text {nc}} A=({\sf tails} A, \pi A)$
where
![]() ${\sf tails} A:={\sf grmod} A/{\sf tors} A$
is the quotient category,
${\sf tails} A:={\sf grmod} A/{\sf tors} A$
is the quotient category,
![]() $\pi :{\sf grmod} A\to {\sf tails} A$
is the quotient functor, and
$\pi :{\sf grmod} A\to {\sf tails} A$
is the quotient functor, and
![]() $A\in {\sf grmod} A$
is the regular graded right module. If A is a d-dimensional quantum polynomial algebra, then we call
$A\in {\sf grmod} A$
is the regular graded right module. If A is a d-dimensional quantum polynomial algebra, then we call
![]() ${\sf Proj}_{\text {nc}} A$
a quantum
${\sf Proj}_{\text {nc}} A$
a quantum
![]() $\mathbb P^{d-1}$
. In particular, if
$\mathbb P^{d-1}$
. In particular, if
![]() $d=3$
, then we call
$d=3$
, then we call
![]() ${\sf Proj}_{\text {nc}} A$
a quantum projective plane.
${\sf Proj}_{\text {nc}} A$
a quantum projective plane.
Note that if A is commutative, then
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj} A$
. It is known that if A is a two-dimensional quantum polynomial algebra, then
${\sf Proj}_{\text {nc}} A\cong {\sf Proj} A$
. It is known that if A is a two-dimensional quantum polynomial algebra, then
 ${\sf Proj}_{\text {nc}} A\cong \mathbb P^{1}$
.
${\sf Proj}_{\text {nc}} A\cong \mathbb P^{1}$
.
For a three-dimensional quantum polynomial algebra
![]() $A=\mathcal A(E, \sigma )$
, we have the following geometric characterization when A is finite over its center.
$A=\mathcal A(E, \sigma )$
, we have the following geometric characterization when A is finite over its center.
Theorem 2.3 [Reference Artin, Tate and Van den Bergh4, Theorem 7.1]
Let
![]() $A=\mathcal {A}(E,\sigma )$
be a three-dimensional quantum polynomial algebra. Then the following are equivalent:
$A=\mathcal {A}(E,\sigma )$
be a three-dimensional quantum polynomial algebra. Then the following are equivalent:
-
(1)
 $|\sigma |<\infty $
.
$|\sigma |<\infty $
. -
(2) A is finite over its center.
Since the property that A is finite over its center is not preserved under isomorphisms of noncommutative projective schemes
![]() ${\sf Proj}_{\text {nc}} A$
, we will make the following rather ad hoc definition.
${\sf Proj}_{\text {nc}} A$
, we will make the following rather ad hoc definition.
Definition 2.6 Let A be a d-dimensional quantum polynomial algebra. We say that
![]() ${\sf Proj}_{\text {nc}}A$
is finite over its center if there exists a d-dimensional quantum polynomial algebra
${\sf Proj}_{\text {nc}}A$
is finite over its center if there exists a d-dimensional quantum polynomial algebra
![]() $A^{\prime }$
finite over its center such that
$A^{\prime }$
finite over its center such that
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
For a three-dimensional quantum polynomial algebra, the above definition coincides with [Reference Mori13, Definition 4.14] by the following result.
Lemma 2.4 [Reference Abdelgadir, Okawa and Ueda1, Corollary A.10]
Let A and
![]() $A^{\prime }$
be three-dimensional quantum polynomial algebras. Then
$A^{\prime }$
be three-dimensional quantum polynomial algebras. Then
![]() ${\sf grmod} A\cong {\sf grmod} A^{\prime }$
if and only if
${\sf grmod} A\cong {\sf grmod} A^{\prime }$
if and only if
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
To characterize “geometric” quantum projective spaces finite over their centers, we will introduce the following notion.
Definition 2.7 [Reference Mori13, Definition 4.6]
For a geometric pair
![]() $(E, \sigma )$
where
$(E, \sigma )$
where
![]() $E\subset \mathbb {P}^{n-1}$
and
$E\subset \mathbb {P}^{n-1}$
and
![]() $\sigma \in \text {Aut}_{k}E$
, we define
$\sigma \in \text {Aut}_{k}E$
, we define
For a geometric pair
![]() $(E, \sigma )$
, clearly
$(E, \sigma )$
, clearly
![]() $\|\sigma \| \leq |\sigma |$
. The following are the basic properties of
$\|\sigma \| \leq |\sigma |$
. The following are the basic properties of
![]() $\|\sigma \|$
.
$\|\sigma \|$
.
Lemma 2.5 [Reference Mori13, Lemma 4.16(1)], [Reference Mori and Ueyama14, Lemma 2.5]
Let A and
![]() $A^{\prime }$
be d-dimensional quantum polynomial algebras satisfying (G1) with
$A^{\prime }$
be d-dimensional quantum polynomial algebras satisfying (G1) with
![]() $\mathcal {P}(A)=(E,\sigma )$
and
$\mathcal {P}(A)=(E,\sigma )$
and
![]() $\mathcal {P}(A^{\prime })=(E^{\prime },\sigma ^{\prime })$
.
$\mathcal {P}(A^{\prime })=(E^{\prime },\sigma ^{\prime })$
.
-
(1) If
 $A\cong A^{\prime }$
, then
$A\cong A^{\prime }$
, then
 $E\cong E^{\prime }$
and
$E\cong E^{\prime }$
and
 $|\sigma |=|\sigma ^{\prime }|$
.
$|\sigma |=|\sigma ^{\prime }|$
. -
(2) If
 $\mathsf{grmod}\,A\cong \mathsf{grmod}\,A^{\prime }$
, then
$\mathsf{grmod}\,A\cong \mathsf{grmod}\,A^{\prime }$
, then
 $E\cong E^{\prime }$
and
$E\cong E^{\prime }$
and
 $||\sigma ||=||\sigma ^{\prime }||$
.
$||\sigma ||=||\sigma ^{\prime }||$
.
In particular, if A and
![]() $A^{\prime }$
are three-dimensional quantum polynomial algebras such that
$A^{\prime }$
are three-dimensional quantum polynomial algebras such that
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
, then
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
, then
![]() $E\cong E^{\prime }$
(that is, A and
$E\cong E^{\prime }$
(that is, A and
![]() $A^{\prime }$
are of the same type) and
$A^{\prime }$
are of the same type) and
![]() $||\sigma ||=||\sigma ^{\prime }||$
.
$||\sigma ||=||\sigma ^{\prime }||$
.
For a three-dimensional quantum polynomial algebra
![]() $A=\mathcal A(E, \sigma )$
of Type S, we have the following geometric characterization when a quantum projective plane
$A=\mathcal A(E, \sigma )$
of Type S, we have the following geometric characterization when a quantum projective plane
![]() ${\sf Proj}_{\text {nc}}A$
is finite over its center.
${\sf Proj}_{\text {nc}}A$
is finite over its center.
Theorem 2.6 [Reference Mori13, Theorem 4.17]
Let
![]() $A=\mathcal {A}(E,\sigma )$
be a three-dimensional quantum polynomial algebra of Type S. Then the following are equivalent:
$A=\mathcal {A}(E,\sigma )$
be a three-dimensional quantum polynomial algebra of Type S. Then the following are equivalent:
-
(1)
 $\|\sigma \|<\infty $
.
$\|\sigma \|<\infty $
. -
(2)
 ${\sf Proj}_{\text {nc}}A$
is finite over its center.
${\sf Proj}_{\text {nc}}A$
is finite over its center.
The purpose of this paper is to extend the above theorem to all types.
2.3 Points of a noncommutative scheme
Definition 2.8 Let R be an algebra. A point of
![]() ${\sf Spec}_{\text {nc}} R$
is an isomorphism class of a simple right R-module
${\sf Spec}_{\text {nc}} R$
is an isomorphism class of a simple right R-module
![]() $M\in {\sf mod} R$
such that
$M\in {\sf mod} R$
such that
![]() $\dim _{k}M<\infty $
. A point M is called fat if
$\dim _{k}M<\infty $
. A point M is called fat if
![]() $\dim _{k}M>1$
.
$\dim _{k}M>1$
.
Remark 2.7 If R is a commutative algebra and
![]() $p\in {\sf Spec} A$
is a closed point, then
$p\in {\sf Spec} A$
is a closed point, then
![]() $A/\mathfrak{m}_{p}\in {\sf mod} R$
is a point where
$A/\mathfrak{m}_{p}\in {\sf mod} R$
is a point where
![]() $\mathfrak{m}_{p}$
is the maximal ideal of R corresponding to p. In fact, this gives a bijection between the set of closed points of
$\mathfrak{m}_{p}$
is the maximal ideal of R corresponding to p. In fact, this gives a bijection between the set of closed points of
![]() ${\sf Spec} R$
and the set of points of
${\sf Spec} R$
and the set of points of
![]() ${\sf Spec}_{\text {nc}} R$
. In this commutative case, there exists no fat point.
${\sf Spec}_{\text {nc}} R$
. In this commutative case, there exists no fat point.
Remark 2.8 Fat points are not preserved under Morita equivalences. For example,
![]() ${\sf mod} k\cong {\sf mod} M_{2}(k)$
, but it is easy to see that
${\sf mod} k\cong {\sf mod} M_{2}(k)$
, but it is easy to see that
![]() ${\sf Spec}_{\text {nc}} k$
has no fat point while
${\sf Spec}_{\text {nc}} k$
has no fat point while
![]() ${\sf Spec}_{\text {nc}} M_{2}(k)$
has a fat point. However, since
${\sf Spec}_{\text {nc}} M_{2}(k)$
has a fat point. However, since
![]() ${\sf Spec}_{\text {nc}} R\cong {\sf Spec}_{\text {nc}} R^{\prime }$
if and only if
${\sf Spec}_{\text {nc}} R\cong {\sf Spec}_{\text {nc}} R^{\prime }$
if and only if
![]() $R\cong R^{\prime }$
, fat points are preserved under isomorphisms of
$R\cong R^{\prime }$
, fat points are preserved under isomorphisms of
![]() ${\sf Spec}_{\text {nc}} R$
.
${\sf Spec}_{\text {nc}} R$
.
Example 2.9 If
![]() $R=k\langle u, v\rangle /(uv-vu-1)$
is the first Weyl algebra, then it is well known that there exists no finite-dimensional right R-module, so
$R=k\langle u, v\rangle /(uv-vu-1)$
is the first Weyl algebra, then it is well known that there exists no finite-dimensional right R-module, so
![]() ${\sf Spec}_{\text {nc}} R$
has no point at all.
${\sf Spec}_{\text {nc}} R$
has no point at all.
Example 2.10 (cf. [Reference Smith15])
If
![]() $R=k\langle u, v\rangle /(vu-uv-u)$
is the enveloping algebra of a two-dimensional nonabelian Lie algebra, then the set of points of
$R=k\langle u, v\rangle /(vu-uv-u)$
is the enveloping algebra of a two-dimensional nonabelian Lie algebra, then the set of points of
![]() ${\sf Spec}_{\text {nc}} R$
is given by
${\sf Spec}_{\text {nc}} R$
is given by
![]() $\{R/uR+(v-\mu )R\}_{\mu \in k}$
, so
$\{R/uR+(v-\mu )R\}_{\mu \in k}$
, so
![]() ${\sf Spec}_{\text {nc}} R$
has no fat point. In fact, the linear map
${\sf Spec}_{\text {nc}} R$
has no fat point. In fact, the linear map
![]() $\delta :k[u]\to k[u]$
defined by
$\delta :k[u]\to k[u]$
defined by
![]() $\delta (f(u))=uf^{\prime }(u)$
is a derivation of
$\delta (f(u))=uf^{\prime }(u)$
is a derivation of
![]() $k[u]$
such that
$k[u]$
such that
![]() $R=k[u][v; \delta ]$
is the Ore extension, so that
$R=k[u][v; \delta ]$
is the Ore extension, so that
![]() $vf(u)=f(u)v+uf^{\prime }(u)$
. If M is a finite-dimensional right R-module, then there exists
$vf(u)=f(u)v+uf^{\prime }(u)$
. If M is a finite-dimensional right R-module, then there exists
![]() $f(u)=a_{d}u^{d}+\cdots +a_{1}u+a_{0}\in k[u]\subset R$
of the minimal degree
$f(u)=a_{d}u^{d}+\cdots +a_{1}u+a_{0}\in k[u]\subset R$
of the minimal degree
![]() $\deg f(u)=d\geq 1$
such that
$\deg f(u)=d\geq 1$
such that
![]() $Mf(u)=0$
. Since
$Mf(u)=0$
. Since
![]() $uf^{\prime }(u)=vf(u)-f(u)v$
,
$uf^{\prime }(u)=vf(u)-f(u)v$
,
![]() $M(df(u)-uf^{\prime }(u))=0$
such that
$M(df(u)-uf^{\prime }(u))=0$
such that
![]() $\deg (df(u)-uf^{\prime }(u))<\deg f(u)$
,
$\deg (df(u)-uf^{\prime }(u))<\deg f(u)$
,
![]() $df(u)=uf^{\prime }(u)$
by minimality of
$df(u)=uf^{\prime }(u)$
by minimality of
![]() $\deg f(u)=d\geq 1$
, but this is possible only if
$\deg f(u)=d\geq 1$
, but this is possible only if
![]() $f(u)=a_{1}u$
, so
$f(u)=a_{1}u$
, so
![]() $Mu=0$
. It follows that M can be viewed as an
$Mu=0$
. It follows that M can be viewed as an
![]() $R/(u)$
-module, a point of
$R/(u)$
-module, a point of
![]() ${\sf Spec}_{\text {nc}} (R/(u))\cong {\sf Spec}_{\text {nc}} k[v]$
, so
${\sf Spec}_{\text {nc}} (R/(u))\cong {\sf Spec}_{\text {nc}} k[v]$
, so
![]() $M\cong R/uR+(v-\mu )R$
for some
$M\cong R/uR+(v-\mu )R$
for some
![]() $\mu \in k$
. Since
$\mu \in k$
. Since
![]() ${\sf Spec}_{\text {nc}} (R/(u))\cong {\sf Spec}_{\text {nc}} k[v]$
is a commutative scheme,
${\sf Spec}_{\text {nc}} (R/(u))\cong {\sf Spec}_{\text {nc}} k[v]$
is a commutative scheme,
![]() ${\sf Spec}_{\text {nc}} R$
has no fat point.
${\sf Spec}_{\text {nc}} R$
has no fat point.
Example 2.11 [Reference Mori13, Lemma 4.19]
If
![]() $R=k\langle u, v\rangle /(uv+vu)$
is a two-dimensional (ungraded) quantum polynomial algebra, then the set of points of
$R=k\langle u, v\rangle /(uv+vu)$
is a two-dimensional (ungraded) quantum polynomial algebra, then the set of points of
![]() ${\sf Spec}_{\text {nc}} R$
is given by
${\sf Spec}_{\text {nc}} R$
is given by
 $$ \begin{align*} \{R/(u-\lambda)R+vR\}_{\lambda\in k}&\cup\{R/uR+(v-\mu)R\}_{\mu\in k}\\ &\cup\{R/(x^{2}-\lambda)R+(\sqrt{\mu}x+\sqrt{-\lambda}y)R+(y^{2}-\mu)R\}_{0\neq \lambda, \, \mu\in k}. \end{align*} $$
$$ \begin{align*} \{R/(u-\lambda)R+vR\}_{\lambda\in k}&\cup\{R/uR+(v-\mu)R\}_{\mu\in k}\\ &\cup\{R/(x^{2}-\lambda)R+(\sqrt{\mu}x+\sqrt{-\lambda}y)R+(y^{2}-\mu)R\}_{0\neq \lambda, \, \mu\in k}. \end{align*} $$
Among them,
 $\{R/(x^{2}-\lambda )R+(\sqrt {\mu }x+\sqrt {-\lambda }y)R+(y^{2}-\mu )R\}_{0\neq \lambda , \, \mu \in k}$
is the set of fat points of
$\{R/(x^{2}-\lambda )R+(\sqrt {\mu }x+\sqrt {-\lambda }y)R+(y^{2}-\mu )R\}_{0\neq \lambda , \, \mu \in k}$
is the set of fat points of
![]() ${\sf Spec}_{\text {nc}} R$
.
${\sf Spec}_{\text {nc}} R$
.
Definition 2.9 Let A be a graded algebra. A point of
![]() ${\sf Proj}_{\text {nc}} A$
is an isomorphism class of a simple object of the form
${\sf Proj}_{\text {nc}} A$
is an isomorphism class of a simple object of the form
![]() $\pi M\in {\sf tails} A$
where
$\pi M\in {\sf tails} A$
where
![]() $M\in {\sf grmod} A$
is a graded right A-module such that
$M\in {\sf grmod} A$
is a graded right A-module such that
![]() $\lim _{i\to \infty }\dim _{k}M_{i}<\infty $
. A point
$\lim _{i\to \infty }\dim _{k}M_{i}<\infty $
. A point
![]() $\pi M$
is called fat if
$\pi M$
is called fat if
![]() $\lim _{i\to \infty } \dim _{k}M_{i}>1$
, and, in this case, M is called a fat point module over A.
$\lim _{i\to \infty } \dim _{k}M_{i}>1$
, and, in this case, M is called a fat point module over A.
Remark 2.12 If A is a graded commutative algebra and
![]() $p\in {\sf Proj} A$
is a closed point, then
$p\in {\sf Proj} A$
is a closed point, then
![]() $\pi (A/\mathfrak m_{p})\in {\sf tails} A$
is a point where
$\pi (A/\mathfrak m_{p})\in {\sf tails} A$
is a point where
![]() $\mathfrak m_{p}$
is the homogeneous maximal ideal of A corresponding to p. In fact, this gives a bijection between the set of closed points of
$\mathfrak m_{p}$
is the homogeneous maximal ideal of A corresponding to p. In fact, this gives a bijection between the set of closed points of
![]() ${\sf Proj} A$
and the set of points of
${\sf Proj} A$
and the set of points of
![]() ${\sf Proj}_{\text {nc}} A$
. In this commutative case, there exists no fat point.
${\sf Proj}_{\text {nc}} A$
. In this commutative case, there exists no fat point.
Remark 2.13 It is unclear that fat points are preserved under isomorphisms of
![]() ${\sf Proj}_{\text {nc}} A$
in general. However, fat point modules are preserved under graded Morita equivalences, so if A and
${\sf Proj}_{\text {nc}} A$
in general. However, fat point modules are preserved under graded Morita equivalences, so if A and
![]() $A^{\prime }$
are both three-dimensional quantum polynomial algebras such that
$A^{\prime }$
are both three-dimensional quantum polynomial algebras such that
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
, then there exists a natural bijection between the set of fat points of
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
, then there exists a natural bijection between the set of fat points of
![]() ${\sf Proj}_{\text {nc}} A$
and that of
${\sf Proj}_{\text {nc}} A$
and that of
![]() ${\sf Proj}_{\text {nc}} A^{\prime }$
by Lemma 2.4.
${\sf Proj}_{\text {nc}} A^{\prime }$
by Lemma 2.4.
The following facts will be used to prove our main results.
Lemma 2.14 [Reference Artin2, Reference Mori13]
Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra.
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra.
-
(1)
 $\|\sigma \|=1$
if and only if
$\|\sigma \|=1$
if and only if
 $E=\mathbb {P}^{2}$
.
$E=\mathbb {P}^{2}$
. -
(2)
 $1<\|\sigma \|<\infty $
if and only if
$1<\|\sigma \|<\infty $
if and only if
 ${\sf Proj}_{\text {nc}} A$
has a fat point.
${\sf Proj}_{\text {nc}} A$
has a fat point.
Theorem 2.15 [Reference Mori13, Theorem 4.20]
If A is a quantum polynomial algebra and
![]() $x\in A$
is a homogeneous normal element of positive degree, then there exists a bijection between the set of points of
$x\in A$
is a homogeneous normal element of positive degree, then there exists a bijection between the set of points of
![]() ${\sf Proj}_{\text {nc}} A$
and the disjoint union of the set of points of
${\sf Proj}_{\text {nc}} A$
and the disjoint union of the set of points of
![]() ${\sf Proj}_{\text {nc}} A/(x)$
and the set of points of
${\sf Proj}_{\text {nc}} A/(x)$
and the set of points of
![]() ${\sf Spec}_{\text {nc}} A[x^{-1}]_{0}$
. In this bijection, fat points correspond to fat points.
${\sf Spec}_{\text {nc}} A[x^{-1}]_{0}$
. In this bijection, fat points correspond to fat points.
3 Main results
In this section, we will state and prove our main results.
Let A be a graded algebra and
![]() $\nu \in \text {Aut} A$
a graded algebra automorphism. For a graded A–A-bimodule M, we define a new graded A–A bimodule
$\nu \in \text {Aut} A$
a graded algebra automorphism. For a graded A–A-bimodule M, we define a new graded A–A bimodule
![]() $M_{\nu }=M$
as a graded vector space with the new actions
$M_{\nu }=M$
as a graded vector space with the new actions
![]() $a*m*b:=am\nu (b)$
for
$a*m*b:=am\nu (b)$
for
![]() $a, b\in A, m\in M$
. Let A be a d-dimensional quantum polynomial algebra. The canonical module of A is defined by
$a, b\in A, m\in M$
. Let A be a d-dimensional quantum polynomial algebra. The canonical module of A is defined by
![]() $\omega _{A}:=\lim _{i\to \infty }\text {Ext}^{d}_{A}(A/A_{\geq i}, A)$
, which has a natural graded A–A bimodule structure. It is known that there exists
$\omega _{A}:=\lim _{i\to \infty }\text {Ext}^{d}_{A}(A/A_{\geq i}, A)$
, which has a natural graded A–A bimodule structure. It is known that there exists
![]() $\nu \in \text {Aut} A$
such that
$\nu \in \text {Aut} A$
such that
![]() $\omega _{A}\cong A_{\nu ^{-1}}(-d)$
as graded A–A bimodules. We call
$\omega _{A}\cong A_{\nu ^{-1}}(-d)$
as graded A–A bimodules. We call
![]() $\nu $
the Nakayama automorphism of A. Since
$\nu $
the Nakayama automorphism of A. Since
![]() $A_{0}=k$
, the Nakayama automorphism
$A_{0}=k$
, the Nakayama automorphism
![]() $\nu $
is uniquely determined by A. Among quantum polynomial algebras, Calabi–Yau quantum polynomial algebras defined below are easier to handle.
$\nu $
is uniquely determined by A. Among quantum polynomial algebras, Calabi–Yau quantum polynomial algebras defined below are easier to handle.
Definition 3.1 A quantum polynomial algebra A is called Calabi–Yau if the Nakayama automorphism of A is the identity.
The following theorem plays an essential role to prove our main results, claiming that every quantum projective plane has a three-dimensional Calabi–Yau quantum polynomial algebra as a homogeneous coordinate ring.
Theorem 3.1 [Reference Itaba and Matsuno8, Theorem 4.4]
For every three-dimensional quantum polynomial algebra A, there exists a three-dimensional Calabi–Yau quantum polynomial algebra
![]() $A^{\prime }$
such that
$A^{\prime }$
such that
![]() ${\sf grmod} A\cong {\sf grmod} A^{\prime }$
, so that
${\sf grmod} A\cong {\sf grmod} A^{\prime }$
, so that
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
.
By the above theorem, the proofs of our main results reduce to the Calabi–Yau case.
3.1 Calabi–Yau case
Let
![]() $E=\mathcal V(x^{3}+y^{3}+z^{3}-\lambda xyz)\subset \mathbb P^{2}, \; \lambda \in k, \lambda ^{3}\neq 27$
be an elliptic curve in the Hesse form. We fix a group structure with the identity element
$E=\mathcal V(x^{3}+y^{3}+z^{3}-\lambda xyz)\subset \mathbb P^{2}, \; \lambda \in k, \lambda ^{3}\neq 27$
be an elliptic curve in the Hesse form. We fix a group structure with the identity element
![]() $o:=(1,-1,0)\in E$
, and write
$o:=(1,-1,0)\in E$
, and write
![]() $E[n]:=\{p\in E\mid np=o\}$
the set of n-torsion points. We also denote by
$E[n]:=\{p\in E\mid np=o\}$
the set of n-torsion points. We also denote by
![]() $\sigma _{p}\in \text {Aut}_{k} E$
the translation automorphism by a point
$\sigma _{p}\in \text {Aut}_{k} E$
the translation automorphism by a point
![]() $p\in E$
. It is known that
$p\in E$
. It is known that
![]() $\sigma _{p}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
$\sigma _{p}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
![]() $p\in E[3]$
(cf. [Reference Mori12, Lemma 5.3]).
$p\in E[3]$
(cf. [Reference Mori12, Lemma 5.3]).
Lemma 3.2 Denote a three-dimensional Calabi–Yau quantum polynomial algebra as
Then Table 1
gives a list of defining relations
![]() $f_{1}, f_{2}, f_{3}$
and the corresponding geometric pairs
$f_{1}, f_{2}, f_{3}$
and the corresponding geometric pairs
![]() $(E,\sigma )$
for such algebras up to isomorphism. In Table 1, we remark that:
$(E,\sigma )$
for such algebras up to isomorphism. In Table 1, we remark that:
-
(1) Type S and Type T are further divided into Type S
 $_{1}$
and Type S
$_{1}$
and Type S
 $_{3}$
, and Type T
$_{3}$
, and Type T
 $_{1}$
and Type T
$_{1}$
and Type T
 $_{3}$
, respectively, in terms of the form of
$_{3}$
, respectively, in terms of the form of
 $\sigma $
.
$\sigma $
. -
(2) The point scheme E may consist of several irreducible components, and, in this case,
 $\sigma $
is described on each component.
$\sigma $
is described on each component. -
(3) For Type NC and Type CC,
 $\sigma $
in Table 1 is defined except for the unique singular point
$\sigma $
in Table 1 is defined except for the unique singular point
 $(0, 0, 1)\in E$
, which is preserved by
$(0, 0, 1)\in E$
, which is preserved by
 $\sigma $
.
$\sigma $
. -
(4) For Type TL and Type WL, E is nonreduced, and the description of
 $\sigma $
is omitted.
$\sigma $
is omitted.
Proof The list of the defining relations
![]() $f_{1}, f_{2}, f_{3}$
is given in [Reference Itaba and Matsuno7, Theorem 3.3] and [Reference Matsuno9, Corollary 4.3]. It is not difficult to calculate their corresponding geometric pairs
$f_{1}, f_{2}, f_{3}$
is given in [Reference Itaba and Matsuno7, Theorem 3.3] and [Reference Matsuno9, Corollary 4.3]. It is not difficult to calculate their corresponding geometric pairs
![]() $(E, \sigma )$
using the condition (G1) (see, for example, [Reference Ueyama16, proof of Theorem 3.1] for Type P, S
$(E, \sigma )$
using the condition (G1) (see, for example, [Reference Ueyama16, proof of Theorem 3.1] for Type P, S
![]() $_{1}$
, S
$_{1}$
, S
![]() $_{3}$
, S’, and [Reference Mori and Ueyama14, proof of Theorem 3.6] for Type T
$_{3}$
, S’, and [Reference Mori and Ueyama14, proof of Theorem 3.6] for Type T
![]() $_{1}$
, T’). We only give some calculations to check that
$_{1}$
, T’). We only give some calculations to check that
![]() $(E, \sigma )$
in Table 1 is correct for Type CC.
$(E, \sigma )$
in Table 1 is correct for Type CC.
Table 1 List of defining relations and the corresponding geometric pairs.


Let
![]() $A=k\langle x,y,z \rangle /(f_{1}, f_{2}, f_{3})$
be a three-dimensional Calabi–Yau quantum polynomial algebra of Type CC where
$A=k\langle x,y,z \rangle /(f_{1}, f_{2}, f_{3})$
be a three-dimensional Calabi–Yau quantum polynomial algebra of Type CC where
and let
![]() $E=\mathcal {V}(x^{3}-y^{2}z)$
, and
$E=\mathcal {V}(x^{3}-y^{2}z)$
, and
 $$ \begin{align*}\sigma(a,b,c)=\begin{cases} \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right) & \text{ if } (a, b, c)\neq (0, 0, 1), \\ (0, 0, 1) & \text{ if } (a, b, c)=(0, 0, 1), \end{cases}\end{align*} $$
$$ \begin{align*}\sigma(a,b,c)=\begin{cases} \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right) & \text{ if } (a, b, c)\neq (0, 0, 1), \\ (0, 0, 1) & \text{ if } (a, b, c)=(0, 0, 1), \end{cases}\end{align*} $$
as in Table 1. If
![]() $p=(a, b, c)\in E$
, then
$p=(a, b, c)\in E$
, then
![]() $a^{3}-b^{2}c=0$
, so
$a^{3}-b^{2}c=0$
, so
 $$ \begin{align*} f_{1}(p, \sigma(p)) &= f_{1}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right) \\ &= \; b\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)-cb+b^{2}+3a(a-b) \\ &= \; -3a^{2}+3ab-b^{2}+bc-bc+b^{2}+3a^{2}-3ab =0, \\ f_{2}(p, \sigma(p)) &= f_{2}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right)\\ &= \; c(a-b)-a\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)+b(a-b)\\ &\quad +ab-b\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)-cb \\ &= \; ac-bc+3\dfrac{a^{3}}{b}-3a^{2}+ab-ac+ab-b^{2}\\ &\quad+ab+3a^{2}-3ab+b^{2}-bc-bc \\ &= \; \dfrac{3}{b}(a^{3}-b^{2}c)=0, \\ f_{3}(p, \sigma(p)) &= f_{3}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right) \\ &= \; ab-b(a-b)-b^{2} = ab-ab+b^{2}-b^{2} = 0, \end{align*} $$
$$ \begin{align*} f_{1}(p, \sigma(p)) &= f_{1}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right) \\ &= \; b\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)-cb+b^{2}+3a(a-b) \\ &= \; -3a^{2}+3ab-b^{2}+bc-bc+b^{2}+3a^{2}-3ab =0, \\ f_{2}(p, \sigma(p)) &= f_{2}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right)\\ &= \; c(a-b)-a\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)+b(a-b)\\ &\quad +ab-b\left(-3\dfrac{a^{2}}{b}+3a-b+c\right)-cb \\ &= \; ac-bc+3\dfrac{a^{3}}{b}-3a^{2}+ab-ac+ab-b^{2}\\ &\quad+ab+3a^{2}-3ab+b^{2}-bc-bc \\ &= \; \dfrac{3}{b}(a^{3}-b^{2}c)=0, \\ f_{3}(p, \sigma(p)) &= f_{3}\left((a, b, c), \left(a-b,b, -3\dfrac{a^{2}}{b}+3a-b+c\right)\right) \\ &= \; ab-b(a-b)-b^{2} = ab-ab+b^{2}-b^{2} = 0, \end{align*} $$
hence
![]() $\{(p, \sigma (p))\in \mathbb P^{2}\times \mathbb P^{2}\mid p\in E\}\subset \mathcal V(f_{1}, f_{2}, f_{3})$
. Since
$\{(p, \sigma (p))\in \mathbb P^{2}\times \mathbb P^{2}\mid p\in E\}\subset \mathcal V(f_{1}, f_{2}, f_{3})$
. Since
![]() $E\subset \mathbb P^{2}$
is a cuspidal cubic curve (and we know that the point scheme of A is not
$E\subset \mathbb P^{2}$
is a cuspidal cubic curve (and we know that the point scheme of A is not
![]() $\mathbb P^{2}$
), E is the point scheme of A, so
$\mathbb P^{2}$
), E is the point scheme of A, so
![]() ${\mathcal P}(A)=(E, \sigma )$
. ▪
${\mathcal P}(A)=(E, \sigma )$
. ▪
Theorem 3.3 If
![]() $A=\mathcal A(E, \sigma )$
is a three-dimensional Calabi–Yau quantum polynomial algebra, then
$A=\mathcal A(E, \sigma )$
is a three-dimensional Calabi–Yau quantum polynomial algebra, then
![]() $||\sigma ||=|\sigma ^{3}|$
, so the following are equivalent:
$||\sigma ||=|\sigma ^{3}|$
, so the following are equivalent:
-
(1)
 $|\sigma |<\infty $
.
$|\sigma |<\infty $
. -
(2)
 $||\sigma ||<\infty $
.
$||\sigma ||<\infty $
. -
(3) A is finite over its center.
-
(4)
 ${\sf Proj}_{\text {nc}} A$
is finite over its center.
${\sf Proj}_{\text {nc}} A$
is finite over its center.
Proof First, we will show that
![]() $||\sigma ||=|\sigma ^{3}|$
for each type using the defining relations
$||\sigma ||=|\sigma ^{3}|$
for each type using the defining relations
![]() $f_{1}, f_{2}, f_{3}$
and geometric pairs
$f_{1}, f_{2}, f_{3}$
and geometric pairs
![]() $(E, \sigma )$
given in Lemma 3.2. Recall that
$(E, \sigma )$
given in Lemma 3.2. Recall that
![]() $\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if it is represented by a matrix in
$\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if it is represented by a matrix in
![]() $\text {PGL}_{3}(k)\cong \text {Aut}_{k} \mathbb P^{2}$
.
$\text {PGL}_{3}(k)\cong \text {Aut}_{k} \mathbb P^{2}$
.
Type P Since
![]() $\sigma ^{3}=\text {id}$
,
$\sigma ^{3}=\text {id}$
,
![]() $||\sigma ||=1=|\sigma ^{3}|$
.
$||\sigma ||=1=|\sigma ^{3}|$
.
![]() $\underline {\text {Type S}_{1}}$
Since
$\underline {\text {Type S}_{1}}$
Since
 $$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,\alpha^{i} c), \\ \sigma^{i}(a,0,c)=(\alpha^{i} a,0,c)=(\alpha^{2i}a, 0, \alpha^{i}c), \\ \sigma^{i}(a,b,0)=(a,\alpha^{i} b,0)=(\alpha^{2i}a, \alpha^{3i}b, 0), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,\alpha^{i} c), \\ \sigma^{i}(a,0,c)=(\alpha^{i} a,0,c)=(\alpha^{2i}a, 0, \alpha^{i}c), \\ \sigma^{i}(a,b,0)=(a,\alpha^{i} b,0)=(\alpha^{2i}a, \alpha^{3i}b, 0), \end{cases} \end{align*} $$
![]() $\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
$\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
![]() $\alpha ^{3i}=1$
, so
$\alpha ^{3i}=1$
, so
![]() $||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
$||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
![]() $\underline {\text {Type S}_{3}}$
Since
$\underline {\text {Type S}_{3}}$
Since
 $$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,\alpha^{i} c)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \\ \sigma^{i}(a,0,c)=(\alpha^{i} a,0,c)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \\ \sigma^{i}(a,b,0)=(a,\alpha^{i} b,0)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,\alpha^{i} c)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \\ \sigma^{i}(a,0,c)=(\alpha^{i} a,0,c)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \\ \sigma^{i}(a,b,0)=(a,\alpha^{i} b,0)\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}^{i}, \end{cases} \end{align*} $$
and
 $\begin {pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end {pmatrix}\in \text {Aut}_{k} (\mathbb P^{2}, E)$
,
$\begin {pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end {pmatrix}\in \text {Aut}_{k} (\mathbb P^{2}, E)$
,
![]() $\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
$\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
![]() $\alpha ^{3i}=1$
, so
$\alpha ^{3i}=1$
, so
![]() $||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
$||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
Type S’ Since
 $$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b, \alpha^{i} c), \\ \sigma^{i}(a,b,c)=(a,\alpha^{i} b,\alpha^{-i} c)=(\alpha^{-i}a, b, \alpha^{-2i}c), \\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b, \alpha^{i} c), \\ \sigma^{i}(a,b,c)=(a,\alpha^{i} b,\alpha^{-i} c)=(\alpha^{-i}a, b, \alpha^{-2i}c), \\ \end{cases} \end{align*} $$
![]() $\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
$\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
![]() $\alpha ^{3i}=1$
, so
$\alpha ^{3i}=1$
, so
![]() $||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
$||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
![]() $\underline {\text {Type T}_{1}}$
Since
$\underline {\text {Type T}_{1}}$
Since
 $$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,ib+c), \\ \sigma^{i}(a,0,c)=(a,0,ia+c), \\ \sigma^{i}(a,a,c)=(a,a,-ia+c), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{i}(0,b,c)=(0,b,ib+c), \\ \sigma^{i}(a,0,c)=(a,0,ia+c), \\ \sigma^{i}(a,a,c)=(a,a,-ia+c), \end{cases} \end{align*} $$
![]() $\sigma ^{i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
$\sigma ^{i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
![]() $i\geq 1$
, so
$i\geq 1$
, so
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
.
$||\sigma ||=\infty =|\sigma ^{3}|$
.
![]() $\underline {\text {Type T}_{3}}$
Since
$\underline {\text {Type T}_{3}}$
Since
 $$ \begin{align*} \begin{cases} \sigma^{3i}(0,b,c)=(0,b,ib+c), \\ \sigma^{3i}(a,0,c)=(a,0, ia+c), \\ \sigma^{3i}(a,a,c)=(a,a,-ia+c), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{3i}(0,b,c)=(0,b,ib+c), \\ \sigma^{3i}(a,0,c)=(a,0, ia+c), \\ \sigma^{3i}(a,a,c)=(a,a,-ia+c), \end{cases} \end{align*} $$
![]() $\sigma ^{3i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
$\sigma ^{3i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
![]() $i\geq 1$
, so
$i\geq 1$
, so
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
.
$||\sigma ||=\infty =|\sigma ^{3}|$
.
Type T’ Since
 $$ \begin{align*} \begin{cases} \sigma^{i}(a,0,c)=(a,0,ia+c), \\ \sigma^{i}(a,b,c)=(a-ib,b,-2ia+i^{2}b+c), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \sigma^{i}(a,0,c)=(a,0,ia+c), \\ \sigma^{i}(a,b,c)=(a-ib,b,-2ia+i^{2}b+c), \end{cases} \end{align*} $$
![]() $\sigma ^{i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
$\sigma ^{i}\not \in \text {Aut}_{k} (\mathbb P^{2}, E)$
for every
![]() $i\geq 1$
, so
$i\geq 1$
, so
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
.
$||\sigma ||=\infty =|\sigma ^{3}|$
.
Type NC Since
 $$ \begin{align*}\sigma^{i}(a, b, c)=\left(a, \alpha^{i} b, -\frac{\alpha^{3i}-1}{\alpha^{i-1}(\alpha^{3}-1)}\frac{a^{2}}{b}+\alpha^{2i} c\right),\end{align*} $$
$$ \begin{align*}\sigma^{i}(a, b, c)=\left(a, \alpha^{i} b, -\frac{\alpha^{3i}-1}{\alpha^{i-1}(\alpha^{3}-1)}\frac{a^{2}}{b}+\alpha^{2i} c\right),\end{align*} $$
![]() $\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
$\sigma ^{i}\in \text {Aut}_{k}(\mathbb P^{2}, E)$
if and only if
![]() $\alpha ^{3i}=1$
, so
$\alpha ^{3i}=1$
, so
![]() $||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
$||\sigma ||=|\alpha ^{3}|=|\sigma ^{3}|$
.
Type CC Since
 $$ \begin{align*}\sigma^{i}(a, b, c)=\left(a-ib, b, -3i\frac{a^{2}}{b}+3i^{2}a-i^{3}b+c\right),\end{align*} $$
$$ \begin{align*}\sigma^{i}(a, b, c)=\left(a-ib, b, -3i\frac{a^{2}}{b}+3i^{2}a-i^{3}b+c\right),\end{align*} $$
![]() $\sigma ^{i}\not \in \text {Aut} (\mathbb P^{2}, E)$
for every
$\sigma ^{i}\not \in \text {Aut} (\mathbb P^{2}, E)$
for every
![]() $i\geq 1$
, so
$i\geq 1$
, so
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
.
$||\sigma ||=\infty =|\sigma ^{3}|$
.
Type TL Since
![]() $A=k\langle x, y, z\rangle /(yz-\alpha zy-x^{2}, zx-\alpha xz, xy-\alpha yx), \; \alpha ^{3}=1$
, we see that
$A=k\langle x, y, z\rangle /(yz-\alpha zy-x^{2}, zx-\alpha xz, xy-\alpha yx), \; \alpha ^{3}=1$
, we see that
![]() $x\in A_{1}$
is a regular normal element. Since
$x\in A_{1}$
is a regular normal element. Since
![]() $A/(x)\cong k\langle y, z\rangle /(yz-\alpha zy)$
is a two-dimensional quantum polynomial algebra,
$A/(x)\cong k\langle y, z\rangle /(yz-\alpha zy)$
is a two-dimensional quantum polynomial algebra,
 ${\sf Proj}_{\text {nc}} A/(x)\cong \mathbb P^{1}$
has no fat point. Since
${\sf Proj}_{\text {nc}} A/(x)\cong \mathbb P^{1}$
has no fat point. Since
![]() $A[x^{-1}]_{0}\cong k\langle u, v\rangle /(uv-vu-\alpha )$
where
$A[x^{-1}]_{0}\cong k\langle u, v\rangle /(uv-vu-\alpha )$
where
![]() $u=yx^{-1}, v=zx^{-1}$
is isomorphic to the first Weyl algebra,
$u=yx^{-1}, v=zx^{-1}$
is isomorphic to the first Weyl algebra,
![]() ${\sf Spec}_{\text {nc}} A[x^{-1}]_{0}$
has no (fat) point by Example 2.9. By Theorem 2.15,
${\sf Spec}_{\text {nc}} A[x^{-1}]_{0}$
has no (fat) point by Example 2.9. By Theorem 2.15,
![]() ${\sf Proj}_{\text {nc}} A$
has no fat point. Since
${\sf Proj}_{\text {nc}} A$
has no fat point. Since
![]() $E\neq \mathbb P^{2}$
,
$E\neq \mathbb P^{2}$
,
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
by Lemma 2.14.
$||\sigma ||=\infty =|\sigma ^{3}|$
by Lemma 2.14.
Type WL Since
![]() $A=k\langle x, y, z\rangle /(yz-zy-(1/3)y^{2}, zx-xz-(1/3)(yx+xy), xy-yx)$
, we see that
$A=k\langle x, y, z\rangle /(yz-zy-(1/3)y^{2}, zx-xz-(1/3)(yx+xy), xy-yx)$
, we see that
![]() $y\in A_{1}$
is a regular normal element. Since
$y\in A_{1}$
is a regular normal element. Since
![]() $A/(y)\cong k[x, z]$
is a two-dimensional (quantum) polynomial algebra,
$A/(y)\cong k[x, z]$
is a two-dimensional (quantum) polynomial algebra,
 ${\sf Proj}_{\text {nc}} A/(y)= \mathbb P^{1}$
has no fat point. Since
${\sf Proj}_{\text {nc}} A/(y)= \mathbb P^{1}$
has no fat point. Since
![]() $A[y^{-1}]_{0}\cong k\langle u, v\rangle /(vu-uv-u)$
where
$A[y^{-1}]_{0}\cong k\langle u, v\rangle /(vu-uv-u)$
where
![]() $u=xy^{-1}, v=zy^{-1}$
is isomorphic to the enveloping algebra of a two-dimensional nonabelian Lie algebra,
$u=xy^{-1}, v=zy^{-1}$
is isomorphic to the enveloping algebra of a two-dimensional nonabelian Lie algebra,
![]() ${\sf Spec}_{\text {nc}} A[y^{-1}]_{0}$
has no fat point by Example 2.10. By Theorem 2.15,
${\sf Spec}_{\text {nc}} A[y^{-1}]_{0}$
has no fat point by Example 2.10. By Theorem 2.15,
![]() ${\sf Proj}_{\text {nc}} A$
has no fat point. Since
${\sf Proj}_{\text {nc}} A$
has no fat point. Since
![]() $E\neq \mathbb P^{2}$
,
$E\neq \mathbb P^{2}$
,
![]() $||\sigma ||=\infty =|\sigma ^{3}|$
by Lemma 2.14.
$||\sigma ||=\infty =|\sigma ^{3}|$
by Lemma 2.14.
Type EC Since
 $\sigma _{p}^{i}=\sigma _{ip}\in \text {Aut}_{k} (\mathbb P^{2}, E)$
if and only if
$\sigma _{p}^{i}=\sigma _{ip}\in \text {Aut}_{k} (\mathbb P^{2}, E)$
if and only if
![]() $ip\in E[3]$
if and only if
$ip\in E[3]$
if and only if
![]() $3ip=o$
,
$3ip=o$
,
 $||\sigma _{p}||=|3p|=|\sigma ^{3}_{p}|$
.
$||\sigma _{p}||=|3p|=|\sigma ^{3}_{p}|$
.
Next, we will show the equivalences (1)
![]() $\Leftrightarrow $
(2)
$\Leftrightarrow $
(2)
![]() $\Leftrightarrow $
(3)
$\Leftrightarrow $
(3)
![]() $\Leftrightarrow $
(4). Since
$\Leftrightarrow $
(4). Since
![]() $||\sigma ||=|\sigma ^{3}|$
for every type, (1)
$||\sigma ||=|\sigma ^{3}|$
for every type, (1)
![]() $\Leftrightarrow $
(2). By Theorem 2.3, (1)
$\Leftrightarrow $
(2). By Theorem 2.3, (1)
![]() $\Leftrightarrow $
(3). By definition, (3)
$\Leftrightarrow $
(3). By definition, (3)
![]() $\Rightarrow $
(4), so it is enough to show that (4)
$\Rightarrow $
(4), so it is enough to show that (4)
![]() $\Rightarrow $
(2). Indeed, if
$\Rightarrow $
(2). Indeed, if
![]() ${\sf Proj}_{\text {nc}}A$
is finite over its center, then there exists a three-dimensional quantum polynomial algebra
${\sf Proj}_{\text {nc}}A$
is finite over its center, then there exists a three-dimensional quantum polynomial algebra
![]() $A^{\prime }=\mathcal {A}(E^{\prime },\sigma ^{\prime })$
which is finite over its center such that
$A^{\prime }=\mathcal {A}(E^{\prime },\sigma ^{\prime })$
which is finite over its center such that
![]() ${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
by Definition 2.6, so
${\sf Proj}_{\text {nc}} A\cong {\sf Proj}_{\text {nc}} A^{\prime }$
by Definition 2.6, so
![]() $\|\sigma \|=\|\sigma ^{\prime }\| \leq $
$\|\sigma \|=\|\sigma ^{\prime }\| \leq $
![]() $|\sigma ^{\prime }|<\infty $
by Lemma 2.5 and Theorem 2.3.▪
$|\sigma ^{\prime }|<\infty $
by Lemma 2.5 and Theorem 2.3.▪
3.2 General case
Definition 3.2 [Reference Mori and Ueyama14, Definition 3.2]
For a d-dimensional geometric quantum polynomial algebra
![]() $A=\mathcal A(E, \sigma )$
with the Nakayama automorphism
$A=\mathcal A(E, \sigma )$
with the Nakayama automorphism
![]() $\nu \in \text {Aut} A$
, we define a new graded algebra
$\nu \in \text {Aut} A$
, we define a new graded algebra
![]() $\overline A:=\mathcal A(E, \nu ^{*}\sigma ^{d})$
satisfying (G2).
$\overline A:=\mathcal A(E, \nu ^{*}\sigma ^{d})$
satisfying (G2).
Lemma 3.4 [Reference Mori and Ueyama14, Theorem 3.5]
Let A and
![]() $A^{\prime }$
be geometric quantum polynomial algebras. If
$A^{\prime }$
be geometric quantum polynomial algebras. If
![]() ${\sf grmod} A\cong {\sf grmod} A^{\prime }$
, then
${\sf grmod} A\cong {\sf grmod} A^{\prime }$
, then
![]() $\overline A\cong \overline {A^{\prime }}$
.
$\overline A\cong \overline {A^{\prime }}$
.
Remark 3.5 If A and
![]() $A^{\prime }$
are both three-dimensional quantum polynomial algebras of the same Type P, S
$A^{\prime }$
are both three-dimensional quantum polynomial algebras of the same Type P, S
![]() $_{1}$
, S’
$_{1}$
, S’
![]() $_{1}$
, T
$_{1}$
, T
![]() $_{1}$
, T’
$_{1}$
, T’
![]() $_{1}$
, then the converse of the above lemma was proved in [Reference Mori and Ueyama14, Theorem 3.6].
$_{1}$
, then the converse of the above lemma was proved in [Reference Mori and Ueyama14, Theorem 3.6].
Theorem 3.6 If
![]() $A=\mathcal A(E, \sigma )$
is a three-dimensional quantum polynomial algebra with the Nakayama automorphism
$A=\mathcal A(E, \sigma )$
is a three-dimensional quantum polynomial algebra with the Nakayama automorphism
![]() $\nu \in \text {Aut} A$
, then
$\nu \in \text {Aut} A$
, then
![]() $||\sigma ||=|\nu ^{*}\sigma ^{3}|$
, so the following are equivalent:
$||\sigma ||=|\nu ^{*}\sigma ^{3}|$
, so the following are equivalent:
-
(1)
 $|\nu ^{*}\sigma ^{3}|<\infty $
.
$|\nu ^{*}\sigma ^{3}|<\infty $
. -
(2)
 $||\sigma ||<\infty $
.
$||\sigma ||<\infty $
. -
(3)
 ${\sf Proj}_{\text {nc}} A$
is finite over its center.
${\sf Proj}_{\text {nc}} A$
is finite over its center.
Moreover, if A is of Type T, T’, CC, TL, WL, then A is never finite over its center.
Proof For every three-dimensional quantum polynomial algebra
![]() $A=\mathcal A(E, \sigma )$
, there exists a three-dimensional Calabi–Yau quantum polynomial algebra
$A=\mathcal A(E, \sigma )$
, there exists a three-dimensional Calabi–Yau quantum polynomial algebra
![]() $A^{\prime }=\mathcal A(E^{\prime }, \sigma ^{\prime })$
such that
$A^{\prime }=\mathcal A(E^{\prime }, \sigma ^{\prime })$
such that
![]() ${\sf grmod} A\cong {\sf grmod} A^{\prime }$
by Theorem 3.1. Since the Nakayama automorphism of
${\sf grmod} A\cong {\sf grmod} A^{\prime }$
by Theorem 3.1. Since the Nakayama automorphism of
![]() $A^{\prime }$
is the identity,
$A^{\prime }$
is the identity,
 $\mathcal A(E, \nu ^{*}\sigma ^{3})\ =\ \overline A \ \cong\ \overline {A^{\prime }}\ =\ \mathcal A(E^{\prime }, {\sigma ^{\prime }}^{3})$
by Lemma 3.4, so
$\mathcal A(E, \nu ^{*}\sigma ^{3})\ =\ \overline A \ \cong\ \overline {A^{\prime }}\ =\ \mathcal A(E^{\prime }, {\sigma ^{\prime }}^{3})$
by Lemma 3.4, so
 $$ \begin{align*}||\sigma||=||\sigma^{\prime}||=|{\sigma^{\prime}}^{3}|=|\nu^{*}\sigma^{3}|\end{align*} $$
$$ \begin{align*}||\sigma||=||\sigma^{\prime}||=|{\sigma^{\prime}}^{3}|=|\nu^{*}\sigma^{3}|\end{align*} $$
by Lemma 2.5 and Theorem 3.3. Since
![]() ${\sf Proj}_{\text {nc}} A$
is finite over its center if and only if
${\sf Proj}_{\text {nc}} A$
is finite over its center if and only if
![]() ${\sf Proj}_{\text {nc}} A^{\prime }$
is finite over its center if and only if
${\sf Proj}_{\text {nc}} A^{\prime }$
is finite over its center if and only if
![]() $||\sigma ^{\prime }||<\infty $
by Theorem 3.3, we have the equivalences (1)
$||\sigma ^{\prime }||<\infty $
by Theorem 3.3, we have the equivalences (1)
![]() $\Leftrightarrow $
(2)
$\Leftrightarrow $
(2)
![]() $\Leftrightarrow $
(3).
$\Leftrightarrow $
(3).
If A is a three-dimensional quantum polynomial algebra of Type T, T’, CC, TL, WL, then
![]() $A^{\prime }$
is of the same type by Lemma 2.5, so
$A^{\prime }$
is of the same type by Lemma 2.5, so
![]() $||\sigma ||=||\sigma ^{\prime }||=\infty $
by the proof of Theorem 3.3. It follows that
$||\sigma ||=||\sigma ^{\prime }||=\infty $
by the proof of Theorem 3.3. It follows that
![]() $|\sigma |=\infty $
, so A is not finite over its center by Theorem 2.3.▪
$|\sigma |=\infty $
, so A is not finite over its center by Theorem 2.3.▪
4 An application to Beilinson algebras
We finally apply our results to representation theory of finite-dimensional algebras.
Definition 4.1 [Reference Herschend, Iyama and Oppermann6, Definition 2.7]
Let R be a finite-dimensional algebra of
![]() $\text {gldim} R=d<\infty $
. We define an autoequivalence
$\text {gldim} R=d<\infty $
. We define an autoequivalence
![]() $\nu _{d}\in \text {Aut} D^{b}({\sf mod} R)$
by
$\nu _{d}\in \text {Aut} D^{b}({\sf mod} R)$
by
![]() $\nu _{d}(M):=M\otimes _{R}^{\text {L}}DR[-d]$
where
$\nu _{d}(M):=M\otimes _{R}^{\text {L}}DR[-d]$
where
![]() $D^{b}({\sf mod} R)$
is the bounded derived category of
$D^{b}({\sf mod} R)$
is the bounded derived category of
![]() ${\sf mod} R$
and
${\sf mod} R$
and
![]() $DR:=\text {Hom}_{k}(R, k)$
. We say that R is d-representation infinite if
$DR:=\text {Hom}_{k}(R, k)$
. We say that R is d-representation infinite if
![]() $\nu _{d}^{-i}(R)\in {\sf mod} R$
for all
$\nu _{d}^{-i}(R)\in {\sf mod} R$
for all
![]() $i\in \mathbb N$
. In this case, we say that a module
$i\in \mathbb N$
. In this case, we say that a module
![]() $M\in {\sf mod} R$
is d-regular if
$M\in {\sf mod} R$
is d-regular if
![]() $\nu _{d}^{i}(M)\in {\sf mod} R$
for all
$\nu _{d}^{i}(M)\in {\sf mod} R$
for all
![]() $i\in \mathbb Z$
.
$i\in \mathbb Z$
.
By [Reference Minamoto10], a
![]() $1$
-representation infinite algebra is exactly the same as a finite-dimensional hereditary algebra of infinite representation type. For representation theory of such an algebra, regular modules play an essential role.
$1$
-representation infinite algebra is exactly the same as a finite-dimensional hereditary algebra of infinite representation type. For representation theory of such an algebra, regular modules play an essential role.
For a d-dimensional quantum polynomial algebra A, we define the Beilinson algebra of A by
 $$ \begin{align*}\nabla A:=\begin{pmatrix} A_{0} & A_{1} & \cdots & A_{d-1} \\ 0 & A_{0} & \cdots & A_{d-2} \\ \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & A_{0} \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\nabla A:=\begin{pmatrix} A_{0} & A_{1} & \cdots & A_{d-1} \\ 0 & A_{0} & \cdots & A_{d-2} \\ \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & A_{0} \end{pmatrix}.\end{align*} $$
The Beilinson algebra is a typical example of a
![]() $(d-1)$
-representation infinite algebra by [Reference Minamoto and Mori11, Theorem 4.12]. To investigate representation theory of such an algebra, it is important to classify simple
$(d-1)$
-representation infinite algebra by [Reference Minamoto and Mori11, Theorem 4.12]. To investigate representation theory of such an algebra, it is important to classify simple
![]() $(d-1)$
-regular modules.
$(d-1)$
-regular modules.
Corollary 4.1 Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra with the Nakayama automorphism
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra with the Nakayama automorphism
![]() $\nu \in \text {Aut} A$
. Then the following are equivalent:
$\nu \in \text {Aut} A$
. Then the following are equivalent:
-
(1)
 $|\nu ^{*}\sigma ^{3}|=1$
or
$|\nu ^{*}\sigma ^{3}|=1$
or
 $\infty $
.
$\infty $
. -
(2)
 ${\sf Proj}_{\text {nc}} A$
has no fat point.
${\sf Proj}_{\text {nc}} A$
has no fat point. -
(3) The isomorphism classes of simple
 $2$
-regular modules over
$2$
-regular modules over
 $\nabla A$
are parameterized by the set of closed points of
$\nabla A$
are parameterized by the set of closed points of
 $E\subset \mathbb P^{2}$
.
$E\subset \mathbb P^{2}$
.
In particular, if A is of P, T, T’, CC, TL, WL, then A satisfies all of the above conditions.
Proof (1)
![]() $\Leftrightarrow $
(2): This follow from Theorem 3.6 and Lemma 2.14.
$\Leftrightarrow $
(2): This follow from Theorem 3.6 and Lemma 2.14.
(2)
![]() $\Leftrightarrow $
(3): By [Reference Mori13, Theorem 3.6], isomorphism classes of simple
$\Leftrightarrow $
(3): By [Reference Mori13, Theorem 3.6], isomorphism classes of simple
![]() $2$
-regular modules over
$2$
-regular modules over
![]() $\nabla A$
are parameterized by the set of points of
$\nabla A$
are parameterized by the set of points of
![]() ${\sf Proj}_{\text {nc}} A$
. On the other hand, it is well known that the points of
${\sf Proj}_{\text {nc}} A$
. On the other hand, it is well known that the points of
![]() ${\sf Proj}_{\text {nc}} A$
which are not fat (called ordinary points in [Reference Mori13]) are parameterized by the set of closed points of E (see [Reference Mori13, Proposition 4.4]); hence, the result holds.▪
${\sf Proj}_{\text {nc}} A$
which are not fat (called ordinary points in [Reference Mori13]) are parameterized by the set of closed points of E (see [Reference Mori13, Proposition 4.4]); hence, the result holds.▪
Remark 4.2 We have the following characterization of Type P, T, T’, CC, TL, WL. Let
![]() $A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. Write
$A=\mathcal A(E, \sigma )$
be a three-dimensional quantum polynomial algebra. Write
![]() $E=\mathcal V(f)\subset \mathbb P^{2}$
where
$E=\mathcal V(f)\subset \mathbb P^{2}$
where
![]() $f\in k[x, y, z]_{3}$
. Recall that the Hessian of f is defined by
$f\in k[x, y, z]_{3}$
. Recall that the Hessian of f is defined by
 $H(f):=\det \begin {pmatrix} f_{xx} & f_{xy} & f_{xz} \\ f_{yx} & f_{yy} & f_{yz} \\ f_{zx} & f_{zy} & f_{zz} \end {pmatrix}\in k[x, y, z]_{3}$
. Then A is of Type P, T, T’, CC, TL, WL if and only if
$H(f):=\det \begin {pmatrix} f_{xx} & f_{xy} & f_{xz} \\ f_{yx} & f_{yy} & f_{yz} \\ f_{zx} & f_{zy} & f_{zz} \end {pmatrix}\in k[x, y, z]_{3}$
. Then A is of Type P, T, T’, CC, TL, WL if and only if
![]() $H^{2}(f):=H(H(f))=0$
.
$H^{2}(f):=H(H(f))=0$
.
Remark 4.3 If A is a two-dimensional quantum polynomial algebra, then
 , so
, so
![]() $\nabla A$
is a finite-dimensional hereditary algebra of tame representation type. It is known that the isomorphism classes of simple regular modules over
$\nabla A$
is a finite-dimensional hereditary algebra of tame representation type. It is known that the isomorphism classes of simple regular modules over
![]() $\nabla A$
are parameterized by
$\nabla A$
are parameterized by
![]() $\mathbb P^{1}$
(cf. [Reference Mori13, Theorem 3.19]). For a three-dimensional quantum polynomial algebra A, we expect that the following are equivalent:
$\mathbb P^{1}$
(cf. [Reference Mori13, Theorem 3.19]). For a three-dimensional quantum polynomial algebra A, we expect that the following are equivalent:
-
(1)
 ${\sf Proj}_{\text {nc}} A$
is finite over its center.
${\sf Proj}_{\text {nc}} A$
is finite over its center. -
(2)
 $\nabla A$
is
$\nabla A$
is
 $2$
-representation tame in the sense of [Reference Herschend, Iyama and Oppermann6].
$2$
-representation tame in the sense of [Reference Herschend, Iyama and Oppermann6]. -
(3) The isomorphism classes of simple
 $2$
-regular modules over
$2$
-regular modules over
 $\nabla A$
are parameterized by
$\nabla A$
are parameterized by
 $\mathbb P^{2}$
.
$\mathbb P^{2}$
.
These equivalences are shown for Type S in [Reference Mori13, Theorems 4.17 and 4.21].