We consider the periodic injection and extraction of fluid from a line well in a horizontal saturated aquifer of finite thickness as part of an aquifer thermal energy storage system. We focus on the case in which the injected fluid is dense relative to the original fluid in the aquifer and we explore the competition between the driving pressure and buoyancy force in controlling the dispersal of the injected fluid through the aquifer. We show that, after each cycle, a progressively larger fraction of the injected fluid is extracted, while the remainder of the injected fluid gradually migrates away from the well such that, after time  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}t$, the position of the leading edge of the injected fluid,
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}t$, the position of the leading edge of the injected fluid, 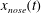 $x_{nose}(t)$, scales as
$x_{nose}(t)$, scales as 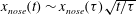 $ x_{nose}(t)\sim x_{nose}(\tau )\sqrt{t/\tau }$, where
$ x_{nose}(t)\sim x_{nose}(\tau )\sqrt{t/\tau }$, where  $\tau $ is the period of injection. If the fluid is extracted from the base of the layer, then, near the well, the thickness of the injected fluid at the end of the extraction cycle tends to a constant value, which decreases with injection rate. We also show that there is a class of self-similar exchange-flow solutions that develop when a saturated porous layer of thickness
$\tau $ is the period of injection. If the fluid is extracted from the base of the layer, then, near the well, the thickness of the injected fluid at the end of the extraction cycle tends to a constant value, which decreases with injection rate. We also show that there is a class of self-similar exchange-flow solutions that develop when a saturated porous layer of thickness 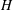 $H$ is in contact with a stratified fluid reservoir, filled to thickness
$H$ is in contact with a stratified fluid reservoir, filled to thickness 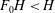 $F_0H<H$ with relatively dense fluid, and with original reservoir fluid above this level. We show that these solutions coincide exactly with the far-field flow produced by the injection–extraction cycles. We successfully test the models with a series of analogue experiments of both the injection–extraction flow and the exchange flow using a Hele-Shaw cell. In the case that the fluid is injected and extracted from the top of the aquifer, the value
$F_0H<H$ with relatively dense fluid, and with original reservoir fluid above this level. We show that these solutions coincide exactly with the far-field flow produced by the injection–extraction cycles. We successfully test the models with a series of analogue experiments of both the injection–extraction flow and the exchange flow using a Hele-Shaw cell. In the case that the fluid is injected and extracted from the top of the aquifer, the value 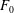 $F_0$ tends to unity in all cases, although the convergence time depends on the rate and period of injection, the buoyancy speed and the vertical extent and the porosity of the aquifer. We use the model to explore how the concentration of reservoir fluid in the produced fluid varies as the system evolves from cycle to cycle, and we also examine the time required to transport a localised but distant contaminant to the production well through the far-field exchange flow. Finally, we consider the analogous axisymmetric injection–extraction flow problem, and show, through both numerical solution of the governing equations and experiment, that, although there is no simple class of similarity solutions, the fraction of injected fluid that is extracted progressively increases in each cycle.
$F_0$ tends to unity in all cases, although the convergence time depends on the rate and period of injection, the buoyancy speed and the vertical extent and the porosity of the aquifer. We use the model to explore how the concentration of reservoir fluid in the produced fluid varies as the system evolves from cycle to cycle, and we also examine the time required to transport a localised but distant contaminant to the production well through the far-field exchange flow. Finally, we consider the analogous axisymmetric injection–extraction flow problem, and show, through both numerical solution of the governing equations and experiment, that, although there is no simple class of similarity solutions, the fraction of injected fluid that is extracted progressively increases in each cycle.