Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T06:36:19.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyant convection from a discrete source in a leaky porous medium

Published online by Cambridge University Press:  14 August 2014

Mark A. Roes ,
Diogo T. Bolster  and
M. R. Flynn
Mark A. Roes
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2G8, Canada
Diogo T. Bolster
Affiliation:
Department of Civil and Environmental Engineering and Earth Sciences, University of Notre Dame, Notre Dame, IN 46556, USA
M. R. Flynn*
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2G8, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The application of turbulent plume theory in describing the dynamics of emptying filling boxes, control volumes connected to an infinite exterior through a series of openings along the upper and lower boundaries, has yielded novel strategies for the natural ventilation of buildings. Making the plume laminar and having it fall through a porous medium yields a problem of fundamental significance in its own right, insights from which may be applied, for example, in minimizing the contamination of drinking water by geologically sequestered 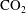$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathrm{CO}}_2$ or the chemicals leached from waste piles. After reviewing the theory appropriate to rectilinear and axisymmetric plumes in porous media, we demonstrate how the model equations may be adapted to the case of an emptying filling box. In this circumstance, the long-time solution consists of two ambient layers, each of which has a uniform density. The lower and upper layers comprise fluid that is respectively discharged by the plume and advected into the box through the upper opening. Our theory provides an estimate for both the height and thickness of the associated interface in terms of, for example, the source volume and buoyancy fluxes, the outlet area and permeability, and the depth-average solute dispersion coefficient, which is itself a function of the far-field horizontal flow speed. Complementary laboratory experiments are provided for the case of a line source plume and show very good agreement with model predictions. Our measurements also indicate that the permeability, 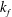$k_f$, of the lower opening (or fissure) decreases with the density of the fluid being discharged, a fact that has been overlooked in some previous studies, wherein 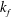$k_f$ is assumed to depend only on the fissure geometry.

JFM classification

Convection: Convection in porous media Low-Reynolds-number flows: Low-Reynolds-number flows Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 204 - 229
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.CrossRefGoogle Scholar
Adalsteinsson, D., Camassa, R., Harenberg, S., Lin, Z., McLaughlin, R. M., Mertens, K., Reis, J., Schlieper, W. & White, B. 2011 Subsurface trapping of oil plumes in stratification: laboratory investigations. In Monitoring and Modeling the Deepwater Horizon Oil Spill (ed. Liu, Y., MacFadyen, A., Ji, Z.-G. & Weisberg, R. H.), Geophysical Monograph Series, vol. 195, pp. 257–262. American Geophysical Union.Google Scholar
Baines, W. D. 1983 Direct measurement of volume flux of a plume. J. Fluid Mech. 132, 247–256.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Barrington, S., Choinière, D., Trigui, M. & Knight, W. 2003 Compost convective airflow under passive aeration. Bioresour. Technol. 86 (3), 259–266.CrossRefGoogle ScholarPubMed
Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bolster, D. T. & Linden, P. F. 2007 Contaminants in ventilated filling boxes. J. Fluid Mech. 591, 97–116.CrossRefGoogle Scholar
Bolster, D. T., Neuweiler, I., Dentz, M. & Carrera, J. 2011 The impact of buoyancy on front spreading in heterogeneous porous media in two-phase immiscible flow. Water Resour. Res. 47 (2), W02508.CrossRefGoogle Scholar
Bower, D. J., Caulfield, C. P., Fitzgerald, S. D. & Woods, A. W. 2008 Transient ventilation dynamics following a change in strength of a point source of heat. J. Fluid Mech. 614, 15–37.Google Scholar
Drysdale, D. 2011 An Introduction to Fire Dynamics. Wiley.CrossRefGoogle Scholar
Fetter, C. W. 1993 Contaminant Hydrogeology. McMillan.Google Scholar
Flynn, M. R. & Caulfield, C. P. 2006 Natural ventilation in interconnected chambers. J. Fluid Mech. 564, 139–158.Google Scholar
Freeze, R. A. & Cherry, J. A. 1979 Groundwater. Prentice-Hall.Google Scholar
Germeles, A. E. 1975 Forced plumes and mixing of liquids in tanks. J. Fluid Mech. 71, 601–623.Google Scholar
Happel, J. & Brenner, H. 1991 Low Reynolds Number Hydrodynamics: with Special Applications to Particulate Media, 2nd edn. Kluwer Academic.Google Scholar
Holford, J. M. & Hunt, G. R. 2001 The dependence of the discharge coefficient on density contrast – experimental measurements. In Proceedings of the 14th Australian Fluid Mechanics Conference, Adelaide University, 10–14 December 2001, pp. 123–126.Google Scholar
Houseworth, J. E.1984 Longitudinal dispersion in non-uniform isotropic porous media. Tech. Rep. KH-R-45. W. M. Keck Laboratory, California Institute of Technology.Google Scholar
Joseph, D. D., Nield, D. A. & Papanicolaou, G. 1982 Nonlinear equation governing flow in a saturated porous medium. Water Resour. Res. 18, 1049–1052.Google Scholar
Kaye, N. B., Flynn, M. R., Cook, M. J. & Ji, Y. 2010 The role of diffusion on the interface thickness in a ventilated filling box. J. Fluid Mech. 652, 195–205.Google Scholar
Kaye, N. B. & Hunt, G. R. 2004 Time-dependent flows in an emptying filling box. J. Fluid Mech. 520, 135–156.CrossRefGoogle Scholar
Kaye, N. B. & Hunt, G. R. 2007 Smoke filling time for a room due to a small fire: the effect of ceiling height to floor width aspect ratio. Fire Safety J. 42 (5), 329–339.CrossRefGoogle Scholar
Killworth, P. D. 1983 Deep convection in the world ocean. Rev. Geophys. 21 (1), 1–26.CrossRefGoogle Scholar
Kuo, E. Y. & Ritchie, A. I. M. 1999 The impact of convection on the overall oxidation rate in sulfidic waste rock dumps. In Proceedings of Mining and the Environment II, 1999, pp. 211–220. Centre in Mining and Mineral Exploration Research.Google Scholar
Lai, F. C. 1991 Non-Darcy natural convection from a line source of heat in a saturated porous medium. Intl Commun. Heat Mass Transfer 18, 445–457.CrossRefGoogle Scholar
Linden, P. F. 1999 The fluid mechanics of natural ventilation. Annu. Rev. Fluid Mech. 31, 201–238.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
McDougall, T. J. 1978 Bubble plumes in stratified environments. J. Fluid Mech. 85 (4), 655–672.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nabi, S. & Flynn, M. R. 2014 Influence of geometric parameters on the eventual buoyancy stratification that develops due to architectural exchange flow. Build. Environ. 71, 33–46.Google Scholar
National Research Council 2012 Alternatives for Managing the Nation’s Complex Contaminated Groundwater Sites. Committee on Future Options for Management in the Nation’s Subsurface Remediation Effort and Water Science and Technology Board (WSTB) and Division on Earth and Life Studies (DELS). The National Academies Press.Google Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.Google Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 1. A localized sink. J. Fluid Mech. 666, 391–413.CrossRefGoogle Scholar
Nield, D. A. & Kuznetsov, A. V. 2013 An historical and topical note on convection in porous media. Trans. ASME: J. Heat Transfer 135, 061201.Google Scholar
Nordbotten, J. M., Celia, M. & Bachu, S. 2004 Analytical solutions for leakage rates through abandoned wells. Water Resour. Res. 40 (4), W04204.CrossRefGoogle Scholar
Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks, 1st edn. Cambridge University Press.Google Scholar
Pritchard, D. & Hogg, A. J. 2002 Draining viscous gravity currents in a vertical fracture. J. Fluid Mech. 459, 207–216.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Roes, M. A.2014 Buoyancy-driven convection in a ventilated porous medium. Master’s thesis, University of Alberta.Google Scholar
Rumpf, H. & Gupte, A. R. 1971 Einflüsse der Porosität und Korngrössenverteilung im Widerstandsgesetz der Porenströmung. Chem. Ing. Tech. 43, 367–375.Google Scholar
Speer, K. G. & Rona, P. A. 1989 A model of an Atlantic and Pacific hydrothermal plume. J. Geophys. Res. Oceans 94 (C5), 6213–6220.CrossRefGoogle Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.Google Scholar
Turcotte, D. L. & Schubert, G. 2014 Geodynamics, 3rd edn. Cambridge University Press.CrossRefGoogle Scholar
Turner, J. S. & Campbell, I. H. 1986 Convection and mixing in magma chambers. Earth-Sci. Rev. 23 (4), 255–352.Google Scholar
Welty, C. & Gelhar, L. W. 1991 Stochastic analysis of the effects of fluid density and viscosity variability on macrodispersion in heterogeneous porous media. Water Resour. Res. 27 (8), 2061–2075.Google Scholar
Wong, A. B. D. & Griffiths, R. W. 2001 Two-basin filling boxes. J. Geophys. Res. Oceans 106, 26929–26941.Google Scholar
Wooding, R. A. 1963 Convection in a saturated porous medium at large Rayleigh number or Péclét number. J. Fluid Mech. 15, 527–544.CrossRefGoogle Scholar
Woods, A. W. 1988 The fluid dynamics and thermodynamics of eruption columns. Bull. Volcanol. 50 (3), 169–193.CrossRefGoogle Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.CrossRefGoogle Scholar
Wüest, A., Brooks, N. H. & Imboden, D. M. 1992 Bubble plume modeling for lake restoration. Water Resour. Res. 28, 3235–3250.CrossRefGoogle Scholar