Published online by Cambridge University Press: 19 August 2014
First, we review analytical and observational studies on third-order structure functions including velocity and buoyancy increments in rotating and stratified turbulence and discuss how these functions can be used in order to estimate the flux of energy through different scales in a turbulent cascade. In particular, we suggest that the negative third-order velocity–temperature–temperature structure function that was measured by Lindborg & Cho (Phys. Rev. Lett., vol. 85, 2000, p. 5663) using stratospheric aircraft data may be used in order to estimate the downscale flux of available potential energy (APE) through the mesoscales. Then, we calculate third-order structure functions from idealized simulations of forced stratified and rotating turbulence and compare with mesoscale results from the lower stratosphere. In the range of scales with a downscale energy cascade of kinetic energy (KE) and APE we find that the third-order structure functions display a negative linear dependence on separation distance  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}} r $, in agreement with observation and supporting the interpretation of the stratospheric data as evidence of a downscale energy cascade. The spectral flux of APE can be estimated from the relevant third-order structure function. However, while the sign of the spectral flux of KE is correctly predicted by using the longitudinal third-order structure functions, its magnitude is overestimated by a factor of two. We also evaluate the third-order velocity structure functions that are not parity invariant and therefore display a cyclonic–anticyclonic asymmetry. In agreement with the results from the stratosphere, we find that these functions have an approximate
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}} r $, in agreement with observation and supporting the interpretation of the stratospheric data as evidence of a downscale energy cascade. The spectral flux of APE can be estimated from the relevant third-order structure function. However, while the sign of the spectral flux of KE is correctly predicted by using the longitudinal third-order structure functions, its magnitude is overestimated by a factor of two. We also evaluate the third-order velocity structure functions that are not parity invariant and therefore display a cyclonic–anticyclonic asymmetry. In agreement with the results from the stratosphere, we find that these functions have an approximate 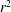 $ r^{2} $-dependence, with strong dominance of cyclonic motions.
$ r^{2} $-dependence, with strong dominance of cyclonic motions.