Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T06:39:36.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow structure on a rotating wing: effect of radius of gyration

Published online by Cambridge University Press:  14 August 2014

M. Wolfinger  and
D. Rockwell
M. Wolfinger
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
D. Rockwell*
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow structure on a rotating wing (flat plate) is characterized over a range of Rossby number 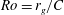$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ro} = r_g/C$, in which 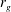$r_g$ and 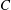$C$ are the radius of gyration and chord of the wing, as well as travel distance $\mathit{Ro} = r_g \Phi /C$, where 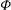$\Phi $ is the angle of rotation. Stereoscopic particle image velocimetry (SPIV) is employed to determine the flow patterns on defined planes, and by means of reconstruction, throughout entire volumes. Images of the 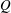$Q$-criterion and spanwise vorticity, velocity and vorticity flux are employed to represent the flow structure. At low Rossby number, the leading-edge, tip and root vortices are highly coherent with large dimensionless values of 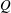$Q$ in the interior regions of all vortices and large downwash between these components of the vortex system. For increasing Rossby number, however, the vortex system rapidly degrades, accompanied by loss of large 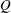$Q$ within its interior and downstream displacement of the region of large downwash. These trends are accompanied by increased deflection of the leading-edge vorticity layer away from the surface of the wing, and decreased spanwise velocity and vorticity flux in the trailing region of the wing, which are associated with the degree of deflection of the tip vortex across the wake region. Combinations of large Rossby number 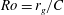$\mathit{Ro} =r_g/C$ and travel distance 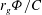$r_g \Phi /C$ lead to separated flow patterns similar to those observed on rectilinear translating wings at high angle of attack $\alpha $. In the extreme case where the wing travels a distance corresponding to a number of revolutions, the highly coherent flow structure is generally preserved if the Rossby number is small; it degrades substantially, however, at larger Rossby number.

JFM classification

Aerodynamics: Aerodynamics Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 83 - 110
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Ansari, S. A., Phillips, N., Stabler, G., Wilkins, P. C., Zbikowski, R. & Knowles, K. 2009 Experimental investigation of some aspects of insect-like flapping flight aerodynamics for application to micro air vehicles. Exp. Fluids 46, 777–798.CrossRefGoogle Scholar
Aono, H., Liang, F. & Liu, H. 2008 Near- and far-field aerodynamics in insect hovering flight: an integrated computational study. J. Expl Biol. 211, 239–257.CrossRefGoogle ScholarPubMed
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412, 729–733.CrossRefGoogle Scholar
Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl Biol. 207, 1063–1072.CrossRefGoogle Scholar
Bomphrey, R. J., Lawson, N. J., Taylor, G. K. & Thomas, A. L. R. 2006 Application of digital particle image velocimetry to insect aerodynamics: measurement of the leading-edge vortex and near wake of a hawkmoth. Exp. Fluids 40, 546–554.CrossRefGoogle Scholar
Bross, M., Ozen, C. A. & Rockwell, D. 2013 Flow structure on a rotating wing: effect of steady incident flow. Phys. Fluids 25, 081901.CrossRefGoogle Scholar
Carr, Z. R., Chen, C. & Ringuette, M. J. 2013 Finite-span rotating wings: three-dimensional vortex formation and variations with aspect ratio. Exp. Fluids 54, 1444.CrossRefGoogle Scholar
Dickinson, M. H. & Götz, K. G. 1993 Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Expl Biol. 174, 45–64.CrossRefGoogle Scholar
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284, 1954–1960.CrossRefGoogle ScholarPubMed
Eldredge, J. D., Wang, C. & Ol, M. V.2009 A computational study of a canonical pitch-up, pitch-down wing maneuver. AIAA Paper 2009-3687.Google Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight I–VI. Phil. Trans. R. Soc. Lond. B 305, 1–181.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 748, 932–956.CrossRefGoogle Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D.2013 Investigation of aspect ratio and dynamic effects due to rotation for a revolving wing using high-fidelity simulation. AIAA Paper 2013-0086.CrossRefGoogle Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.CrossRefGoogle Scholar
Hill, M. J. M. 1894 On a spherical vortex. Phil. Trans. R. Soc. Lond. 185, 213–245.Google Scholar
Hubel, T. Y. & Tropea, C. 2009 Experimental investigation of a flapping wing model. Exp. Fluids 46, 945–961.CrossRefGoogle Scholar
Hunt, J. C., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2, pp. 193–208.Google Scholar
Jardin, T., Farcy, A. & David, L. 2012 Three-dimensional effects in hovering flapping flight. J. Fluid Mech. 702, 102–125.CrossRefGoogle Scholar
Jones, A. R. & Babinsky, H. 2011 Reynolds number effects on leading edge vortex development on a waving wing. Exp. Fluids 51, 197–210.CrossRefGoogle Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49, 329–339.CrossRefGoogle Scholar
Kweon, J. & Choi, H. 2010 Sectional lift coefficient of a flapping wing in hovering motion. Phys. Fluids 22, 071703.CrossRefGoogle Scholar
Lawson, N. J. & Wu, J. 1997 Three-dimensional particle image velocimetry: error analysis of stereoscopic techniques. Meas. Sci. Technol. 8, 894–900.CrossRefGoogle Scholar
Lentink, D. & Dickinson, M. H. 2009a Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Expl Biol. 212, 2691–2704.CrossRefGoogle ScholarPubMed
Lentink, D. & Dickinson, M. H. 2009b Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.CrossRefGoogle ScholarPubMed
Liu, H., Ellington, C. P., Kawachi, K., van den Berg, C. & Willmott, A. P. 1998 A computational fluid dynamic study of hawkmoth hovering. J. Expl Biol. 201, 461–477.CrossRefGoogle ScholarPubMed
Lu, Y. & Shen, G. X. 2008 Three-dimensional flow structures and evolution of the leading-edge vortices on a flapping wing. J. Expl Biol. 211, 1221–1230.CrossRefGoogle Scholar
Luo, G. & Sun, M. 2005 The effects of corrugation and wing planform on the aerodynamic force production of sweeping model insect wings. Acta Mechanica Sin. 21, 531–541.CrossRefGoogle Scholar
Mayo, D. B. & Jones, A. R.2013 Evolution and breakdown of a leading edge vortex on a rotating wing. AIAA Paper 2013-0843.CrossRefGoogle Scholar
Ozen, C. A. & Rockwell, D. 2011 Flow structure on a rotating plate. Exp. Fluids 52, 207–223.CrossRefGoogle Scholar
Ozen, C. A. & Rockwell, D. 2012 Three-dimensional vortex structure on a rotating wing. J. Fluid Mech. 707, 541–550.CrossRefGoogle Scholar
Pines, D. J. & Bohorquez, F. 2006 Challenges facing future micro-air-vehicle development. J. Aircraft 43, 290–305.CrossRefGoogle Scholar
Poelma, C., Dickson, W. B. & Dickinson, M. H. 2006 Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Exp. Fluids 41, 213–225.CrossRefGoogle Scholar
Prasad, A. K. 2000 Stereoscopic particle image velocimetry. Exp. Fluids 29, 103–116.CrossRefGoogle Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206, 4191–4208.CrossRefGoogle ScholarPubMed
Sane, S. P. & Dickinson, M. H. 2001 The control of flight force by a flapping wing: lift and drag production. J. Expl Biol. 204, 2607–2626.CrossRefGoogle ScholarPubMed
Schlueter, K., Jones, A. R., Granlund, K. & Ol, M. 2014 Effect of root cutout on force coefficients of rotating wings. AIAA J. 52 (6), 1322–1325.CrossRefGoogle Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C. K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46, 284–327.CrossRefGoogle Scholar
Sun, M. & Tang, J. 2002 Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J. Expl Biol. 205, 55–70.CrossRefGoogle Scholar
Usherwood, J. R. & Ellington, C. P. 2002a The aerodynamics of revolving wings I. Model hawkmoth wings. J. Expl Biol. 205, 1547–1564.CrossRefGoogle ScholarPubMed
Usherwood, J. R. & Ellington, C. P. 2002b The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Expl Biol. 205, 1565–1576.CrossRefGoogle ScholarPubMed
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.CrossRefGoogle Scholar
Willmott, A. P. & Ellington, C. P. 1997a The mechanics of flight in the hawkmoth manduca sexta. I. Kinematics of hovering and forward flight. J. Expl Biol. 200, 2705–2722.CrossRefGoogle ScholarPubMed
Willmott, A. P. & Ellington, C. P. 1997b The mechanics of flight in the hawkmoth manduca sexta. II. Aerodynamic consequences of kinematic and morphological variation. J. Expl Biol. 200, 2723–2745.CrossRefGoogle ScholarPubMed
Wojcik, C. J. & Buchholz, J. H. J. 2014 Vorticity transport in the leading-edge vortex on a rotating blade. J. Fluid Mech. 743, 249–261.CrossRefGoogle Scholar