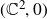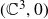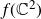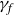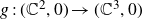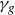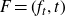1. Introduction
Throughout this paper, we assume that
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow(\mathbb{C}^3,0)$
is a finite, generically
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow(\mathbb{C}^3,0)$
is a finite, generically
![]() $1-1$
, holomorphic map germ, unless otherwise stated. If f has corank 1, local coordinates can be chosen so that these map germs can be written in the form
$1-1$
, holomorphic map germ, unless otherwise stated. If f has corank 1, local coordinates can be chosen so that these map germs can be written in the form
for some function germs
![]() $p,q \in m_2^2$
, where
$p,q \in m_2^2$
, where
![]() $m_2$
is the maximal ideal of the local ring of holomorphic function germs in two variables
$m_2$
is the maximal ideal of the local ring of holomorphic function germs in two variables
![]() $\mathcal{O}_2$
.
$\mathcal{O}_2$
.
In [
Reference Marar and Nuño–Ballesteros12
], Nuño–Ballesteros and Marar studied the generic hyperplane sections of
![]() $f(\mathbb{C}^2)$
, usually called, the transversal slice of f (see Definition 3·1). They showed that if a certain genericity condition is satisfied, then the transverse slice curve
$f(\mathbb{C}^2)$
, usually called, the transversal slice of f (see Definition 3·1). They showed that if a certain genericity condition is satisfied, then the transverse slice curve
![]() $\gamma_f$
contains some information on the geometry of f.
$\gamma_f$
contains some information on the geometry of f.
In this paper, we consider a corank 1, finitely determined, quasi-homogeneous map germ
![]() $f(x,y)=(x,p(x,y),q(x,y))$
from
$f(x,y)=(x,p(x,y),q(x,y))$
from
![]() $(\mathbb{C}^2,0)$
to
$(\mathbb{C}^2,0)$
to
![]() $(\mathbb{C}^3,0)$
. To illustrate the problem that we will present, consider the map germs:
$(\mathbb{C}^3,0)$
. To illustrate the problem that we will present, consider the map germs:
which are the singularities
![]() $P_3$
and
$P_3$
and
![]() $H_2$
of Mond’s list [
Reference Mond16
, p. 378], respectively. Note that both
$H_2$
of Mond’s list [
Reference Mond16
, p. 378], respectively. Note that both
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are corank 1, finitely determined and quasi-homogeneous map germs.
$f_2$
are corank 1, finitely determined and quasi-homogeneous map germs.
Denote by (X, Y, Z) the coordinates of
![]() $\mathbb{C}^3$
and consider the hyperplane H given by the equation
$\mathbb{C}^3$
and consider the hyperplane H given by the equation
![]() $X=0$
. Note that the hyperplanes sections
$X=0$
. Note that the hyperplanes sections
![]() $H\cap f_1(\mathbb{C}^2)$
and
$H\cap f_1(\mathbb{C}^2)$
and
![]() $H\cap f_2(\mathbb{C}^2)$
of
$H\cap f_2(\mathbb{C}^2)$
of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are reduced plane curves parametrised by
$f_2$
are reduced plane curves parametrised by
![]() $u \mapsto (u^3,u^4)$
and
$u \mapsto (u^3,u^4)$
and
![]() $u\mapsto (u^3,u^5)$
, respectively. One can check that
$u\mapsto (u^3,u^5)$
, respectively. One can check that
![]() $H\cap f_1(\mathbb{C}^2)$
is in fact the transversal slice of f, in the sense that it satisfies the transversality conditions of [
Reference Marar and Nuño–Ballesteros12
, section 3]. However, in [
Reference Marar and Nuño–Ballesteros12
, example 5·2], Marar and Nuño–Ballesteros showed that
$H\cap f_1(\mathbb{C}^2)$
is in fact the transversal slice of f, in the sense that it satisfies the transversality conditions of [
Reference Marar and Nuño–Ballesteros12
, section 3]. However, in [
Reference Marar and Nuño–Ballesteros12
, example 5·2], Marar and Nuño–Ballesteros showed that
![]() $H\cap g(\mathbb{C}^2)$
is not the transversal slice of
$H\cap g(\mathbb{C}^2)$
is not the transversal slice of
![]() $f_2$
. This means that the hyperplane H defined by
$f_2$
. This means that the hyperplane H defined by
![]() $X=0$
is not a generic plane for
$X=0$
is not a generic plane for
![]() $f_2$
in the sense of [
Reference Marar and Nuño–Ballesteros12
, section 3]. On the other hand, there are germs of diffeomorphism
$f_2$
in the sense of [
Reference Marar and Nuño–Ballesteros12
, section 3]. On the other hand, there are germs of diffeomorphism
![]() $\Phi:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^2,0)$
and
$\Phi:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^2,0)$
and
![]() $\Psi: (\mathbb{C}^3,0)\rightarrow (\mathbb{C}^3,0)$
such that
$\Psi: (\mathbb{C}^3,0)\rightarrow (\mathbb{C}^3,0)$
such that
![]() $g= \Psi \circ f_2 \circ \Phi$
, where
$g= \Psi \circ f_2 \circ \Phi$
, where
In other words, we have that
![]() $f_2$
is
$f_2$
is
![]() $\mathcal{A}$
-equivalent to g. Furthermore, now the hyperplane
$\mathcal{A}$
-equivalent to g. Furthermore, now the hyperplane
![]() $H=V(X)$
is generic for g. So, the transversal slice of g is the reduced plane curve parametrised by
$H=V(X)$
is generic for g. So, the transversal slice of g is the reduced plane curve parametrised by
![]() $u\mapsto (u^3,u^4)$
. We conclude that the embedded topological type of the transversal slice of
$u\mapsto (u^3,u^4)$
. We conclude that the embedded topological type of the transversal slice of
![]() $f_2$
is the same as the plane curve parametrised by
$f_2$
is the same as the plane curve parametrised by
![]() $u\mapsto (u^3,u^4)$
.
$u\mapsto (u^3,u^4)$
.
This example shows that for a corank 1, finitely determined, quasi-homogeneous map germ in the normal form (1) the plane H defined by
![]() $X=0$
may not be generic for f. Since the embedded topological type of the transversal slice of f does not depend on the choice of the coordinates (see [
Reference Pellikaan22
]), a solution to fix this inconvenience is to work with the
$X=0$
may not be generic for f. Since the embedded topological type of the transversal slice of f does not depend on the choice of the coordinates (see [
Reference Pellikaan22
]), a solution to fix this inconvenience is to work with the
![]() $\mathcal{A}$
-equivalence. However, as illustrated in the above example, when we compose a quasi-homogeneous map germ with germs of diffeormorphisms in the source and target we may lose the property of the resulting composite map being quasi-homogeneous (in relation to the new coordinate system). That seems to mean that the embedded topological type of the transversal slice curve of f is not related to the quasi-homogeneous type of f. So, the following question is natural:
$\mathcal{A}$
-equivalence. However, as illustrated in the above example, when we compose a quasi-homogeneous map germ with germs of diffeormorphisms in the source and target we may lose the property of the resulting composite map being quasi-homogeneous (in relation to the new coordinate system). That seems to mean that the embedded topological type of the transversal slice curve of f is not related to the quasi-homogeneous type of f. So, the following question is natural:
Question 1. Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ on the form (1), i.e.,
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ on the form (1), i.e.,
![]() $f(x,y)=(x,p(x,y),q(x,y))$
. Is the embedded topological type of the transversal slice
$f(x,y)=(x,p(x,y),q(x,y))$
. Is the embedded topological type of the transversal slice
![]() $\gamma_f$
of f determined by the weights of x and y and the weighted degrees of p and q?
$\gamma_f$
of f determined by the weights of x and y and the weighted degrees of p and q?
We know that if f has corank 1, then
![]() $\gamma_f$
is an irreducible plane curve. It is well known that for an irreducible plane curve the characteristic exponents determine and are determined by the embedded topological type of the curve. Thus Question 1 can be reformulated in terms of the characteristic exponents of
$\gamma_f$
is an irreducible plane curve. It is well known that for an irreducible plane curve the characteristic exponents determine and are determined by the embedded topological type of the curve. Thus Question 1 can be reformulated in terms of the characteristic exponents of
![]() $\gamma_f$
. That is, we can ask if the characteristic exponents of
$\gamma_f$
. That is, we can ask if the characteristic exponents of
![]() $\gamma_f$
are determined by the weights and degrees of f. In the first part of this paper, we present a positive answer to Question 1, (see Propositions 3·5 and 3·10). We show that the number of characteristic exponents of
$\gamma_f$
are determined by the weights and degrees of f. In the first part of this paper, we present a positive answer to Question 1, (see Propositions 3·5 and 3·10). We show that the number of characteristic exponents of
![]() $\gamma_f$
can only be two or three, depending on some relations between the weights and degrees of f. More precisely, we show the following result:
$\gamma_f$
can only be two or three, depending on some relations between the weights and degrees of f. More precisely, we show the following result:
Theorem 1·1.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ. Write f in the normal form
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ. Write f in the normal form
and let a,b be the weights of the variables x,y, respectively. Let
![]() $ d_2$
and
$ d_2$
and
![]() $d_3$
be the weighted degrees of p and q, respectively, with
$d_3$
be the weighted degrees of p and q, respectively, with
![]() $2 \leq d_2\leq d_3$
. Set
$2 \leq d_2\leq d_3$
. Set
![]() $c=min\lbrace a,d_2 \rbrace$
. Then:
$c=min\lbrace a,d_2 \rbrace$
. Then:
If
![]() $a\leq d_2$
,
$a\leq d_2$
,
![]() $4\leq {d_2}/{b}$
and
$4\leq {d_2}/{b}$
and
![]() $gcd(d_2,d_3)=2$
, then
$gcd(d_2,d_3)=2$
, then
![]() $\gamma_f$
has three characteristic exponents given by
$\gamma_f$
has three characteristic exponents given by
Otherwise,
![]() $\gamma_f$
has only two characteristic exponents given by
$\gamma_f$
has only two characteristic exponents given by
where
Clearly when
![]() $\gamma_f$
has three characteristic exponents it is not a quasi-homogeneous curve. However, we note that the number s in Theorem 1·1 is determined by the weights and degrees of f (see Remark 3·11). In this way, Theorem 1·1 shows that in fact the embedded topological type of the transversal slice of f is determined by the weights and degrees of f, even in the case where the curve
$\gamma_f$
has three characteristic exponents it is not a quasi-homogeneous curve. However, we note that the number s in Theorem 1·1 is determined by the weights and degrees of f (see Remark 3·11). In this way, Theorem 1·1 shows that in fact the embedded topological type of the transversal slice of f is determined by the weights and degrees of f, even in the case where the curve
![]() $\gamma_f$
is not quasi-homogeneous.
$\gamma_f$
is not quasi-homogeneous.
In the second part of this work, we present two natural consequences of Theorem 1·1. More precisely, in Section 4 we show that a necessary condition for a corank 1 finitely determined map germ
![]() $g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
to be quasi-homogeneous (in a suitable system of coordinates) is that the transversal slice of g must be have either two or three characteristic exponents (Corollary 4·1).
$g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
to be quasi-homogeneous (in a suitable system of coordinates) is that the transversal slice of g must be have either two or three characteristic exponents (Corollary 4·1).
Also in Section 4, we show that any one-parameter unfolding
![]() $F=(f_t,t)$
of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular (Corollary 4·4). We also consider some natural questions and provide counterexamples for them. For instance, we show that Question 1 has a negative answer in corank 2 case (see Example 4·6). We also show that Question 1 has a negative answer for corank 1 map germs from
$F=(f_t,t)$
of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular (Corollary 4·4). We also consider some natural questions and provide counterexamples for them. For instance, we show that Question 1 has a negative answer in corank 2 case (see Example 4·6). We also show that Question 1 has a negative answer for corank 1 map germs from
![]() $(\mathbb{C}^n,0) \rightarrow (\mathbb{C}^{n+1},0)$
with
$(\mathbb{C}^n,0) \rightarrow (\mathbb{C}^{n+1},0)$
with
![]() $n\geq 3$
(see Example 4·7). We finish presenting examples to illustrates our results, more precisely, we describe the embedded topological type of any quasi-homogeneous map germ of Mond’s list (see Section 4).
$n\geq 3$
(see Example 4·7). We finish presenting examples to illustrates our results, more precisely, we describe the embedded topological type of any quasi-homogeneous map germ of Mond’s list (see Section 4).
2. Preliminaries
Throughout this paper, given a finite map
![]() $f\,{:}\,\mathbb{C}^2\rightarrow \mathbb{C}^3$
, (x, y) and (X, Y, Z) are used to denote systems of coordinates in
$f\,{:}\,\mathbb{C}^2\rightarrow \mathbb{C}^3$
, (x, y) and (X, Y, Z) are used to denote systems of coordinates in
![]() $\mathbb{C}^2$
(source) and
$\mathbb{C}^2$
(source) and
![]() $\mathbb{C}^3$
(target), respectively. Also,
$\mathbb{C}^3$
(target), respectively. Also,
![]() $\mathbb{C} \lbrace x_1,\ldots,x_n \rbrace \simeq \mathcal{O}_n$
denotes the local ring of convergent power series in n variables. The letters U,V and W are used to denote open neighbourhoods of 0 in
$\mathbb{C} \lbrace x_1,\ldots,x_n \rbrace \simeq \mathcal{O}_n$
denotes the local ring of convergent power series in n variables. The letters U,V and W are used to denote open neighbourhoods of 0 in
![]() $\mathbb{C}^2$
,
$\mathbb{C}^2$
,
![]() $\mathbb{C}^3$
and
$\mathbb{C}^3$
and
![]() $\mathbb{C}$
, respectively. For unfoldings, we will use T to denote the parameter space, which is also an open neighbourhood of 0 in
$\mathbb{C}$
, respectively. For unfoldings, we will use T to denote the parameter space, which is also an open neighbourhood of 0 in
![]() $\mathbb{C}$
. Throughout, we use the standard notation of singularity theory as the reader can find in Wall’s survey paper [
Reference Wall29
], see also [
Reference Mond and Nuño–Ballesteros19
].
$\mathbb{C}$
. Throughout, we use the standard notation of singularity theory as the reader can find in Wall’s survey paper [
Reference Wall29
], see also [
Reference Mond and Nuño–Ballesteros19
].
2·1. Double point curves for corank 1 map germs
In this section, we deal only with of corank 1 map germs. We follow [ Reference Marar and Mond14 , section 1] and [ Reference Mond17 , section 3].
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a finite corank 1 map germ. As we said in Introduction, up to
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a finite corank 1 map germ. As we said in Introduction, up to
![]() $\mathcal{A}-$
equivalence, f can be written in the form
$\mathcal{A}-$
equivalence, f can be written in the form
![]() $f(x,y)=(x,p(x,y),q(x,y))$
. In this case, the lifting of the double point space is defined as:
$f(x,y)=(x,p(x,y),q(x,y))$
. In this case, the lifting of the double point space is defined as:
where (
![]() $x,y,x',y'$
) are coordinates of
$x,y,x',y'$
) are coordinates of
![]() $\mathbb{C}^2 \times \mathbb{C}^2$
and
$\mathbb{C}^2 \times \mathbb{C}^2$
and
![]() $V(h_1,\ldots,h_l)$
denotes the set of common zeros of
$V(h_1,\ldots,h_l)$
denotes the set of common zeros of
![]() $h_1, \ldots, h_l$
.
$h_1, \ldots, h_l$
.
Once the lifting
![]() $D^2(f) \subset \mathbb{C}^2 \times \mathbb{C}^2$
is defined, we now consider its image on
$D^2(f) \subset \mathbb{C}^2 \times \mathbb{C}^2$
is defined, we now consider its image on
![]() $\mathbb{C}^2$
by the projection
$\mathbb{C}^2$
by the projection
![]() $\pi:\mathbb{C}^2 \times \mathbb{C}^2 \rightarrow \mathbb{C}^2$
onto the first factor, which will be denoted by D(f). For our purposes, the most appropriate structure for D(f) is the one given by the Fitting ideals, because it relates in a simple way the properties of the spaces
$\pi:\mathbb{C}^2 \times \mathbb{C}^2 \rightarrow \mathbb{C}^2$
onto the first factor, which will be denoted by D(f). For our purposes, the most appropriate structure for D(f) is the one given by the Fitting ideals, because it relates in a simple way the properties of the spaces
![]() $D^2(f)$
and D(f). Also, this structure is well behaved by deformations.
$D^2(f)$
and D(f). Also, this structure is well behaved by deformations.
More precisely, given a finite morphism of complex spaces
![]() $g:X\rightarrow Y$
the push-forward
$g:X\rightarrow Y$
the push-forward
![]() $g_{\ast}\mathcal{O}_{X}$
is a coherent sheaf of
$g_{\ast}\mathcal{O}_{X}$
is a coherent sheaf of
![]() $\mathcal{O}_{Y}-$
modules (see [
Reference Grauert and Remmert10
, chapter 1]) and to it we can (as in [
Reference Mond and Pellikaan20
, section 1]) associate the Fitting ideal sheaves
$\mathcal{O}_{Y}-$
modules (see [
Reference Grauert and Remmert10
, chapter 1]) and to it we can (as in [
Reference Mond and Pellikaan20
, section 1]) associate the Fitting ideal sheaves
![]() $\mathcal{F}_{k}(g_{\ast}\mathcal{O}_{X})$
. Notice that the support of
$\mathcal{F}_{k}(g_{\ast}\mathcal{O}_{X})$
. Notice that the support of
![]() $\mathcal{F}_{0}(g_{\ast}\mathcal{O}_{X})$
is just the image g(X). Analogously, if
$\mathcal{F}_{0}(g_{\ast}\mathcal{O}_{X})$
is just the image g(X). Analogously, if
![]() $g:(X,x)\rightarrow(Y,y)$
is a finite map germ then we denote also by
$g:(X,x)\rightarrow(Y,y)$
is a finite map germ then we denote also by
![]() $ \mathcal{F}_{k}(g_{\ast}\mathcal{O}_{X})$
the kth Fitting ideal of
$ \mathcal{F}_{k}(g_{\ast}\mathcal{O}_{X})$
the kth Fitting ideal of
![]() $\mathcal{O}_{X,x}$
as
$\mathcal{O}_{X,x}$
as
![]() $\mathcal{O}_{Y,y}-$
module.
$\mathcal{O}_{Y,y}-$
module.
Another important space to study the topology of
![]() $f(\mathbb{C}^{2})$
is the double point curve in the target, that is, the image of D(f) by f, denoted by f(D(f)), which will also be consider with the structure given by Fitting ideals. In this way, we have the following definition:
$f(\mathbb{C}^{2})$
is the double point curve in the target, that is, the image of D(f) by f, denoted by f(D(f)), which will also be consider with the structure given by Fitting ideals. In this way, we have the following definition:
Definition 2·1. Let
![]() $f\,{:}\,U \subset \mathbb{C}^2 \rightarrow V \subset \mathbb{C}^3 $
be a finite mapping.
$f\,{:}\,U \subset \mathbb{C}^2 \rightarrow V \subset \mathbb{C}^3 $
be a finite mapping.
-
(a) Let
 ${\pi}|_{D^2(f)}:D^2(f) \subset U \times U \rightarrow U$
be the restriction to
${\pi}|_{D^2(f)}:D^2(f) \subset U \times U \rightarrow U$
be the restriction to
 $D^2(f)$
of the projection
$D^2(f)$
of the projection
 $\pi$
. The double point space is the complex space
$\pi$
. The double point space is the complex space \begin{align*}D(f)=V(\mathcal{F}_{0}({\pi}_{\ast}\mathcal{O}_{D^2(f)})).\end{align*}
\begin{align*}D(f)=V(\mathcal{F}_{0}({\pi}_{\ast}\mathcal{O}_{D^2(f)})).\end{align*}
Set theoretically we have the equality
![]() $D(f)=\pi(D^{2}(f))$
.
$D(f)=\pi(D^{2}(f))$
.
-
(b) The double point space in the target is the complex space
 $f(D(f))=V(\mathcal{F}_{1}(f_{\ast}\mathcal{O}_2))$
. Notice that the underlying set of
$f(D(f))=V(\mathcal{F}_{1}(f_{\ast}\mathcal{O}_2))$
. Notice that the underlying set of
 $f(D(f))$
is the image of
$f(D(f))$
is the image of
 $D(f)$
by f.
$D(f)$
by f. -
(c) Given a finite map germ
 $f\,{:}\,(\mathbb{C}^{2},0)\rightarrow (\mathbb{C}^3,0)$
, the germ of the double point space is the germ of complex space
$f\,{:}\,(\mathbb{C}^{2},0)\rightarrow (\mathbb{C}^3,0)$
, the germ of the double point space is the germ of complex space
 $D(f)=V(F_{0}(\pi_{\ast}\mathcal{O}_{D^2(f)}))$
. The germ of the double point space in the target is the germ of the complex space
$D(f)=V(F_{0}(\pi_{\ast}\mathcal{O}_{D^2(f)}))$
. The germ of the double point space in the target is the germ of the complex space
 $f(D(f))=V(F_{1}(f_{\ast}\mathcal{O}_2))$
.
$f(D(f))=V(F_{1}(f_{\ast}\mathcal{O}_2))$
.
Remark 2·2. If
![]() $f\,{:}\,U \subset \mathbb{C}^2 \rightarrow V \subset \mathbb{C}^3 $
is finite and generically 1-to-1, then
$f\,{:}\,U \subset \mathbb{C}^2 \rightarrow V \subset \mathbb{C}^3 $
is finite and generically 1-to-1, then
![]() $D^2(f)$
is Cohen–Macaulay and has dimension 1 (see [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, proposition 2·1]). Hence,
$D^2(f)$
is Cohen–Macaulay and has dimension 1 (see [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, proposition 2·1]). Hence,
![]() $D^2(f)$
,
$D^2(f)$
,
![]() $D(f)$
and
$D(f)$
and
![]() $f(D(f))$
are curves. In this case, without any confusion, we also call these complex spaces by the “lifting of the double point curve”, the “double point curve” and the “image of the double point curve”, respectively.
$f(D(f))$
are curves. In this case, without any confusion, we also call these complex spaces by the “lifting of the double point curve”, the “double point curve” and the “image of the double point curve”, respectively.
2·2. Finite determinacy and the invariant C(f)
Definition 2·3.
-
(a) Two map germs
 $f,g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
are
$f,g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
are
 $\mathcal{A}$
-equivalent, denoted by
$\mathcal{A}$
-equivalent, denoted by
 $g\sim_{\mathcal{A}}f$
, if there exist germs of diffeomorphisms
$g\sim_{\mathcal{A}}f$
, if there exist germs of diffeomorphisms
 $\Phi:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^2,0)$
and
$\Phi:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^2,0)$
and
 $\Psi:(\mathbb{C}^3,0)\rightarrow (\mathbb{C}^3,0)$
, such that
$\Psi:(\mathbb{C}^3,0)\rightarrow (\mathbb{C}^3,0)$
, such that
 $g=\Psi \circ f \circ \Phi$
.
$g=\Psi \circ f \circ \Phi$
. -
(b) A map germ
 $f\,{:}\,(\mathbb{C}^2,0) \rightarrow (\mathbb{C}^3,0)$
is finitely determined (
$f\,{:}\,(\mathbb{C}^2,0) \rightarrow (\mathbb{C}^3,0)$
is finitely determined (
 $\mathcal{A}$
-finitely determined) if there exists a positive integer k such that for any g with k-jets satisfying
$\mathcal{A}$
-finitely determined) if there exists a positive integer k such that for any g with k-jets satisfying
 $j^kg(0)=j^kf(0)$
we have
$j^kg(0)=j^kf(0)$
we have
 $g \sim_{\mathcal{A}}f$
.
$g \sim_{\mathcal{A}}f$
.
Remark 2·4. Consider a finite map germ
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
. By Mather–Gaffney criterion ([
Reference Wall29
, theorem 2·1]), f is finitely determined if and only if there is a finite representative
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
. By Mather–Gaffney criterion ([
Reference Wall29
, theorem 2·1]), f is finitely determined if and only if there is a finite representative
![]() $f\,{:}\,U \rightarrow V$
, where
$f\,{:}\,U \rightarrow V$
, where
![]() $U\subset \mathbb{C}^2$
,
$U\subset \mathbb{C}^2$
,
![]() $V \subset \mathbb{C}^3$
are open neighbourhoods of the origin, such that
$V \subset \mathbb{C}^3$
are open neighbourhoods of the origin, such that
![]() $f^{-1}(0)=\lbrace 0 \rbrace$
and the restriction
$f^{-1}(0)=\lbrace 0 \rbrace$
and the restriction
![]() $f\,{:}\,U \setminus \lbrace 0 \rbrace \rightarrow V \setminus \lbrace 0 \rbrace$
is stable.
$f\,{:}\,U \setminus \lbrace 0 \rbrace \rightarrow V \setminus \lbrace 0 \rbrace$
is stable.
This means that the only singularities of f on
![]() $U \setminus \lbrace 0 \rbrace$
are cross-caps (or Whitney umbrellas), transverse double and triple points. By shrinking U if necessary, we can assume that there are no cross-caps nor triple points in U. Then, since we are in the nice dimensions of Mather ([
Reference Mather15
, p. 208]), we can take a stabilisation of f,
$U \setminus \lbrace 0 \rbrace$
are cross-caps (or Whitney umbrellas), transverse double and triple points. By shrinking U if necessary, we can assume that there are no cross-caps nor triple points in U. Then, since we are in the nice dimensions of Mather ([
Reference Mather15
, p. 208]), we can take a stabilisation of f,
where T is a neighbourhood of 0 in
![]() $\mathbb{C}$
. It is well known that the number
$\mathbb{C}$
. It is well known that the number
![]() $C(f)\,{:\!=}\, \sharp $
of cross-caps of
$C(f)\,{:\!=}\, \sharp $
of cross-caps of
![]() $f_t$
is independent of the particular choice of the stabilisation and it is also an analytic invariant of f (see for instance [
Reference Mond16
]). One can calculate C(f) as the codimension of the ramification ideal J(f) in
$f_t$
is independent of the particular choice of the stabilisation and it is also an analytic invariant of f (see for instance [
Reference Mond16
]). One can calculate C(f) as the codimension of the ramification ideal J(f) in
![]() $\mathcal{O}_2$
, that is:
$\mathcal{O}_2$
, that is:
We remark that the space D(f) plays a fundamental role in the study of the finite determinacy. In [
Reference Marar and Mond14
, theorem 2·14], Marar and Mond presented necessary and sufficient conditions for a map germ
![]() $f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^p,0)$
with corank 1 to be finitely determined in terms of the dimensions of
$f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^p,0)$
with corank 1 to be finitely determined in terms of the dimensions of
![]() $D^2(f)$
and other multiple points spaces. In [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
], Marar, Nuño–Ballesteros and Peñafort–Sanchis extended this criterion of finite determinacy to the corank 2 case. They proved the following result.
$D^2(f)$
and other multiple points spaces. In [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
], Marar, Nuño–Ballesteros and Peñafort–Sanchis extended this criterion of finite determinacy to the corank 2 case. They proved the following result.
Theorem 2·5. ([
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
,
Reference Marar and Mond14
]) Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow(\mathbb{C}^{3},0)$
be a finite and generically 1
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow(\mathbb{C}^{3},0)$
be a finite and generically 1
![]() $-$
1 map germ. Then f is finitely determined if and only if the Milnor number of D(f) at 0 is finite.
$-$
1 map germ. Then f is finitely determined if and only if the Milnor number of D(f) at 0 is finite.
2·3. Identification and fold components of D(f)
When
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is finitely determined, the restriction
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is finitely determined, the restriction
![]() $f_{|D(f)}$
of (a representative) f to D(f) is generically 2-to-1 (i.e; 2-to-1 except at 0). On the other hand, the restriction of f to an irreducible component
$f_{|D(f)}$
of (a representative) f to D(f) is generically 2-to-1 (i.e; 2-to-1 except at 0). On the other hand, the restriction of f to an irreducible component
![]() $D(f)^i$
of D(f) is either generically 1-to-1 or generically 2-to-1. This motivates us to give the following definition which is from [
Reference Silva27
, definition 4·1] (see also [
Reference Ruas and Silva24
, definition 2·4]).
$D(f)^i$
of D(f) is either generically 1-to-1 or generically 2-to-1. This motivates us to give the following definition which is from [
Reference Silva27
, definition 4·1] (see also [
Reference Ruas and Silva24
, definition 2·4]).
Definition 2·6. Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a finitely determined map germ. Let
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a finitely determined map germ. Let
![]() $f\,{:}\,U\rightarrow V$
be a representative of f and consider an irreducible component
$f\,{:}\,U\rightarrow V$
be a representative of f and consider an irreducible component
![]() $D(f)^j$
of D(f).
$D(f)^j$
of D(f).
-
(a) If the restriction
 ${f_|}_{D(f)^j}:D(f)^j\rightarrow V$
is generically 1
${f_|}_{D(f)^j}:D(f)^j\rightarrow V$
is generically 1
 $-$
1, we say that
$-$
1, we say that
 $D(f)^j$
is an identification component of D(f). In this case, there exists an irreducible component
$D(f)^j$
is an identification component of D(f). In this case, there exists an irreducible component
 $D(f)^i$
of D(f), with
$D(f)^i$
of D(f), with
 $i \neq j$
, such that
$i \neq j$
, such that
 $f(D(f)^j)=f(D(f)^i)$
. We say that
$f(D(f)^j)=f(D(f)^i)$
. We say that
 $D(f)^i$
is the associated identification component to
$D(f)^i$
is the associated identification component to
 $D(f)^j$
or that the pair
$D(f)^j$
or that the pair
 $(D(f)^j, D(f)^i)$
is a pair of identification components of D(f).
$(D(f)^j, D(f)^i)$
is a pair of identification components of D(f). -
(b) If the restriction
 ${f_|}_{D(f)^j}:D(f)^j\rightarrow V$
is generically 2
${f_|}_{D(f)^j}:D(f)^j\rightarrow V$
is generically 2
 $-$
1, we say that
$-$
1, we say that
 $D(f)^j$
is a fold component of D(f).
$D(f)^j$
is a fold component of D(f).
We would like to remark that the terminology “fold component” in Definition 2·6(b) was chosen by the author in [
Reference Silva27
, definition 4·1] in analogy to the restriction of f to
![]() $D(f)=V(x)$
when f is the cross-cap
$D(f)=V(x)$
when f is the cross-cap
![]() $f(x,y)=(x,y^2,xy)$
, which is a fold map germ. The following example illustrates the two types of irreducible components of D(f) presented in Definition 2·6.
$f(x,y)=(x,y^2,xy)$
, which is a fold map germ. The following example illustrates the two types of irreducible components of D(f) presented in Definition 2·6.
Example 2·7. Let
![]() $f(x,y)=(x,y^2,xy^3-x^5y)$
be the singularity
$f(x,y)=(x,y^2,xy^3-x^5y)$
be the singularity
![]() $C_5$
of Mond’s list [
Reference Mond17
]. Note that
$C_5$
of Mond’s list [
Reference Mond17
]. Note that
![]() $D(f)=V(xy^2-x^5)$
. Thus we have that D(f) has three irreducible components given by
$D(f)=V(xy^2-x^5)$
. Thus we have that D(f) has three irreducible components given by
Notice that
![]() $D(f)^3$
is a fold component and
$D(f)^3$
is a fold component and
![]() $(D(f)^1$
,
$(D(f)^1$
,
![]() $D(f)^2)$
is a pair of identification components. Also, we have that
$D(f)^2)$
is a pair of identification components. Also, we have that
![]() $f(D(f)^3)=V(X,Z)$
and
$f(D(f)^3)=V(X,Z)$
and
![]() $f(D(f)^1)=f(D(f)^2)=V(Y-X^4,Z)$
(see Figure 1).
$f(D(f)^1)=f(D(f)^2)=V(Y-X^4,Z)$
(see Figure 1).

Fig 1. Identification and fold components of D(f) (real points).
3. The slice of a quasi-homogeneous map germ from
 $\mathbb{C}^2$
to
$\mathbb{C}^2$
to
 $\mathbb{C}^3$
$\mathbb{C}^3$
![]() $ \ \ \ \ $
In [
Reference Marar and Nuño–Ballesteros12
], Marar and Nuño–Ballesteros studied the generic hyperplane sections of
$ \ \ \ \ $
In [
Reference Marar and Nuño–Ballesteros12
], Marar and Nuño–Ballesteros studied the generic hyperplane sections of
![]() $f(\mathbb{C}^2)$
for a map germ map germ f from
$f(\mathbb{C}^2)$
for a map germ map germ f from
![]() $(\mathbb{C}^2,0)$
to
$(\mathbb{C}^2,0)$
to
![]() $(\mathbb{C}^3,0)$
of corank 1. Following their paper, in this section we present their notion of transversal slice for f.
$(\mathbb{C}^3,0)$
of corank 1. Following their paper, in this section we present their notion of transversal slice for f.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finite and generically
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finite and generically
![]() $1-1$
holomorphic map germ. In this case, the image of the differential
$1-1$
holomorphic map germ. In this case, the image of the differential
![]() $df_0(\mathbb{C}^2)$
is a line in
$df_0(\mathbb{C}^2)$
is a line in
![]() $\mathbb{C}^3$
through the origin. Also, as we said in Remark 2·2, the double point space in the target f(D(f)) is a curve in
$\mathbb{C}^3$
through the origin. Also, as we said in Remark 2·2, the double point space in the target f(D(f)) is a curve in
![]() $\mathbb{C}^3$
.
$\mathbb{C}^3$
.
Definition 3·1. We say that a plane
![]() $H_0 \subset \mathbb{C}^3$
through the origin is generic for f if the following three conditions hold:
$H_0 \subset \mathbb{C}^3$
through the origin is generic for f if the following three conditions hold:
-
(1)
 $H_0 \cap df_0(\mathbb{C}^2)=\lbrace 0 \rbrace$
,
$H_0 \cap df_0(\mathbb{C}^2)=\lbrace 0 \rbrace$
, -
(2)
 $H_0 \cap f(D(f))=\lbrace 0 \rbrace$
, and
$H_0 \cap f(D(f))=\lbrace 0 \rbrace$
, and -
(3)
 $H_0 \cap C_0(f(D(f)))=\lbrace 0 \rbrace$
,
$H_0 \cap C_0(f(D(f)))=\lbrace 0 \rbrace$
,
where
![]() $C_0(f(D(f)))$
denotes the Zariski tangent cone of f(D(f)) at 0.
$C_0(f(D(f)))$
denotes the Zariski tangent cone of f(D(f)) at 0.
We remark that the set of generic planes for f is a non-empty Zariski open subset of the Grasmannian of planes of
![]() $\mathbb{C}^3$
. In general, the analytic type of the curve
$\mathbb{C}^3$
. In general, the analytic type of the curve
![]() $H\cap f(\mathbb{C}^2)$
may depend on the choice of the coordinates and the generic plane H, but its embedded topological type does not (see [
Reference Pellikaan22
]). Hence, for a generic plane H we will denote the plane curve
$H\cap f(\mathbb{C}^2)$
may depend on the choice of the coordinates and the generic plane H, but its embedded topological type does not (see [
Reference Pellikaan22
]). Hence, for a generic plane H we will denote the plane curve
![]() $H\cap f(\mathbb{C}^2)$
by
$H\cap f(\mathbb{C}^2)$
by
![]() $\gamma_f$
(or
$\gamma_f$
(or
![]() $\gamma$
, for short, if the context is clear) and it usual to call it the transverse slice of f.
$\gamma$
, for short, if the context is clear) and it usual to call it the transverse slice of f.
We would like to study the transversal slice of quasi-homogeneous map germs. Thus, it is convenient to present a precise definition of this kind of map.
Definition 3·2. A polynomial
![]() $p(x_1,\ldots,x_n)$
is quasi-homogeneous if there are positive integers
$p(x_1,\ldots,x_n)$
is quasi-homogeneous if there are positive integers
![]() $w_1,\ldots,w_n$
, with no common factor and an integer d such that
$w_1,\ldots,w_n$
, with no common factor and an integer d such that
![]() $p(k^{w_1}x_1,\ldots,k^{w_n}x_x)=k^dp(x_1,\ldots,x_n)$
. The number
$p(k^{w_1}x_1,\ldots,k^{w_n}x_x)=k^dp(x_1,\ldots,x_n)$
. The number
![]() $w_i$
is called the weight of the variable
$w_i$
is called the weight of the variable
![]() $x_i$
and d is called the weighted degree of p. In this case, we say p is of type
$x_i$
and d is called the weighted degree of p. In this case, we say p is of type
![]() $(d; w_1,\ldots,w_n)$
.
$(d; w_1,\ldots,w_n)$
.
Definition 3·2. extends to polynomial map germs
![]() $f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^p,0)$
by just requiring each coordinate function
$f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^p,0)$
by just requiring each coordinate function
![]() $f_i$
to be quasi-homogeneous of type
$f_i$
to be quasi-homogeneous of type
![]() $(d_i; w_1,\ldots,w_n)$
, for fixed weights
$(d_i; w_1,\ldots,w_n)$
, for fixed weights
![]() $w_1,\ldots,w_n$
. In particular, for a quasi-homogeneous map germ
$w_1,\ldots,w_n$
. In particular, for a quasi-homogeneous map germ
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
we say that it is quasi-homogeneous of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
we say that it is quasi-homogeneous of type
![]() $(d_1,d_2,d_3; w_1,w_2)$
.
$(d_1,d_2,d_3; w_1,w_2)$
.
Note that if
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is a corank 1 quasi-homogeneous map germ in the normal form (1), then we can write
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is a corank 1 quasi-homogeneous map germ in the normal form (1), then we can write
![]() $p(x,y)=\lambda_1 y^n +x\tilde{p}(x,y)$
and
$p(x,y)=\lambda_1 y^n +x\tilde{p}(x,y)$
and
![]() $q(x,y)=\lambda_2y^m+x\tilde{q}(x,y)$
, for some
$q(x,y)=\lambda_2y^m+x\tilde{q}(x,y)$
, for some
![]() $n,m \in \mathbb{N}$
,
$n,m \in \mathbb{N}$
,
![]() $\lambda_i \in \mathbb{C}$
and
$\lambda_i \in \mathbb{C}$
and
![]() $\tilde{p},\tilde{q} \in \mathcal{O}_2$
with
$\tilde{p},\tilde{q} \in \mathcal{O}_2$
with
![]() $\tilde{p}(x,0)=\tilde{q}(x,0)=0$
. This is explained more precisely in the following lemma, where a normal form for f which is more convenient for our purposes is presented. To simplify the notation, in the following we will write p,q in place of
$\tilde{p}(x,0)=\tilde{q}(x,0)=0$
. This is explained more precisely in the following lemma, where a normal form for f which is more convenient for our purposes is presented. To simplify the notation, in the following we will write p,q in place of
![]() $\tilde{p},\tilde{q}$
and set
$\tilde{p},\tilde{q}$
and set
![]() $a\,{:\!=}\, w_1$
and
$a\,{:\!=}\, w_1$
and
![]() $b\,{:\!=}\, w_2$
which will certainly not cause notation confusion.
$b\,{:\!=}\, w_2$
which will certainly not cause notation confusion.
Lemma 3·3. ([
Reference Silva26
, Lemma 2·11]). Let
![]() $g(x,y)=(g_1(x,y),g_2(x,y),g_3(x,y))$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$g(x,y)=(g_1(x,y),g_2(x,y),g_3(x,y))$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1,d_2,d_3; a,b)$
. Then g is
$(d_1,d_2,d_3; a,b)$
. Then g is
![]() $\mathcal{A}$
-equivalent to a quasi-homogeneous map germ f with type
$\mathcal{A}$
-equivalent to a quasi-homogeneous map germ f with type
![]() $(d_{i_1}=a,d_{i_2},d_{i_3};a,b)$
, which is written in the form
$(d_{i_1}=a,d_{i_2},d_{i_3};a,b)$
, which is written in the form
for some integers
![]() $n,m\geq 2$
,
$n,m\geq 2$
,
![]() $\beta \in \mathbb{C}$
,
$\beta \in \mathbb{C}$
,
![]() $p,q \in \mathcal{O}_2$
,
$p,q \in \mathcal{O}_2$
,
![]() $p(x,0)=q(x,0)=0$
, where
$p(x,0)=q(x,0)=0$
, where
![]() $(d_{i_1},d_{i_2},d_{i_3})$
is a permutation of
$(d_{i_1},d_{i_2},d_{i_3})$
is a permutation of
![]() $(d_1,d_2,d_3)$
such that
$(d_1,d_2,d_3)$
such that
![]() $d_{i_2}\leq d_{i_3}$
.
$d_{i_2}\leq d_{i_3}$
.
In the sequel,
![]() $\mu(X,0)$
and m(X,0) denotes respectively the Milnor number and the multiplicity of X at 0. The multiplicity of f is the multiplicity of
$\mu(X,0)$
and m(X,0) denotes respectively the Milnor number and the multiplicity of X at 0. The multiplicity of f is the multiplicity of
![]() $f(\mathbb{C}^2)$
at 0. We note that if f is in the normal form (3), then
$f(\mathbb{C}^2)$
at 0. We note that if f is in the normal form (3), then
![]() $m(f(\mathbb{C}^2))=n$
. In this way, we divide the proof of Theorem 1·1 into two parts. In the first part we present a proof of the result in the case where the multiplicity of f is 2 (see Proposition 3·5). In the second part we deal with the case of multiplicity greater than 2 (see Proposition 3·10). In both cases, we will need the following lemma.
$m(f(\mathbb{C}^2))=n$
. In this way, we divide the proof of Theorem 1·1 into two parts. In the first part we present a proof of the result in the case where the multiplicity of f is 2 (see Proposition 3·5). In the second part we deal with the case of multiplicity greater than 2 (see Proposition 3·10). In both cases, we will need the following lemma.
Lemma 3·4.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1=a,d_2,d_3;a,b)$
, with
$(d_1=a,d_2,d_3;a,b)$
, with
![]() $d_2\leq d_3$
, and write it as in Lemma 3·3
, that is, in the form
$d_2\leq d_3$
, and write it as in Lemma 3·3
, that is, in the form
Let
![]() $\gamma$
be the transversal slice of f. Then
$\gamma$
be the transversal slice of f. Then
where
![]() $c=min\lbrace a,d_2 \rbrace$
,
$c=min\lbrace a,d_2 \rbrace$
,
![]() $s=0$
if the restriction of f to the line
$s=0$
if the restriction of f to the line
![]() $x=0$
is generically
$x=0$
is generically
![]() $1-$
to
$1-$
to
![]() $-1$
or
$-1$
or
![]() $s=1$
, otherwise.
$s=1$
, otherwise.
Proof. Since
![]() $(f^{-1}(\gamma),0)$
is a germ of smooth curve in
$(f^{-1}(\gamma),0)$
is a germ of smooth curve in
![]() $(\mathbb{C}^2,0)$
,
$(\mathbb{C}^2,0)$
,
![]() $\mu(f^{-1}(\gamma),0)=0$
. Now the proof follows by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, lemma 5·2] and [
Reference Silva26
, theorem 3·2].
$\mu(f^{-1}(\gamma),0)=0$
. Now the proof follows by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, lemma 5·2] and [
Reference Silva26
, theorem 3·2].
3·1. The case of multiplicity 2
The following result gives us a positive answer for Question 1 in the case where the multiplicity of f is 2.
Proposition 3·5.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1=a,d_2,d_3;a,b)$
, with
$(d_1=a,d_2,d_3;a,b)$
, with
![]() $d_2\leq d_3$
and suppose that f has multiplicity 2. Write f as in Lemma 3·3
, that is, in the form
$d_2\leq d_3$
and suppose that f has multiplicity 2. Write f as in Lemma 3·3
, that is, in the form
Let
![]() $\gamma$
be the transversal slice of f. Then
$\gamma$
be the transversal slice of f. Then
![]() $\gamma$
has only two characteristic exponents given by
$\gamma$
has only two characteristic exponents given by
where
![]() $c=min\lbrace a,d_2 \rbrace$
,
$c=min\lbrace a,d_2 \rbrace$
,
![]() $s=0$
if the restriction of f to the line
$s=0$
if the restriction of f to the line
![]() $x=0$
is generically
$x=0$
is generically
![]() $1-$
to
$1-$
to
![]() $-1$
or
$-1$
or
![]() $s=1$
, otherwise.
$s=1$
, otherwise.
Proof. Since f has multiplicity 2,
![]() $\gamma$
is a plane curve with multiplicity 2. Therefore,
$\gamma$
is a plane curve with multiplicity 2. Therefore,
![]() $\gamma$
has only two characteristic exponents, namely, 2 and k with
$\gamma$
has only two characteristic exponents, namely, 2 and k with
![]() $2<k$
odd. By Lemma 3·4 we have that
$2<k$
odd. By Lemma 3·4 we have that
where
![]() $c=min\lbrace a,d_2 \rbrace$
and
$c=min\lbrace a,d_2 \rbrace$
and
![]() $s=0$
if
$s=0$
if
![]() $\beta \neq 0$
and m is odd, or
$\beta \neq 0$
and m is odd, or
![]() $s=1$
, otherwise. By expression (4) we conclude that
$s=1$
, otherwise. By expression (4) we conclude that
since in this case we have that
![]() $d_2=2b$
.
$d_2=2b$
.
When we look to the characteristic exponents of
![]() $\gamma$
in Proposition 3·5, we identify four situations depending on the values that c and s may assume. The following example shows that these four situations can occur.
$\gamma$
in Proposition 3·5, we identify four situations depending on the values that c and s may assume. The following example shows that these four situations can occur.
Example 3·6. (
![]() $c=d_2$
and
$c=d_2$
and
![]() $s=1$
) Consider the map germ
$s=1$
) Consider the map germ
which is quasi-homogeneous of type
![]() $(4,2,9; 4,1)$
. We have that
$(4,2,9; 4,1)$
. We have that
![]() $D(f)=V(x(x-y^4))$
which is reduced. So, by Theorem 2·5 we have that f is finitely determined. Using Proposition 3·5 we obtain that the characteristic exponents of
$D(f)=V(x(x-y^4))$
which is reduced. So, by Theorem 2·5 we have that f is finitely determined. Using Proposition 3·5 we obtain that the characteristic exponents of
![]() $\gamma$
are 2 and 5. Note that in this case the plane
$\gamma$
are 2 and 5. Note that in this case the plane
![]() $H=V(X)$
contains an irreducible component of f(D(f)) (see Figure 2).
$H=V(X)$
contains an irreducible component of f(D(f)) (see Figure 2).

Fig 2. The surface
![]() $f(\mathbb{C}^2)$
and the plane
$f(\mathbb{C}^2)$
and the plane
![]() $H=V(X)$
(real points).
$H=V(X)$
(real points).
We will illustrates the other cases in Table 3 (see Section 4). For instance, consider the
![]() $F_4$
-singularity of Mond’s list [
Reference Mond17
], which corresponds to the case where
$F_4$
-singularity of Mond’s list [
Reference Mond17
], which corresponds to the case where
![]() $c=a$
and
$c=a$
and
![]() $s=0$
. For the case where
$s=0$
. For the case where
![]() $c=a$
and
$c=a$
and
![]() $s=1$
consider the cross-cap given by
$s=1$
consider the cross-cap given by
![]() $f(x,y)=(x,y^2,xy)$
. Finally, for the case where
$f(x,y)=(x,y^2,xy)$
. Finally, for the case where
![]() $c=d_2$
and
$c=d_2$
and
![]() $s=0$
consider the
$s=0$
consider the
![]() $B_3$
-singularity of of Mond’s list.
$B_3$
-singularity of of Mond’s list.
3·2. The case of multiplicity greater than 2
In this section we will present a proof of Theorem 1·1 in the case where the multiplicity of f is greater than 2. Note that if
![]() $n=m(f(\mathbb{C}^2))\geq 3$
in Lemma 3·3, then
$n=m(f(\mathbb{C}^2))\geq 3$
in Lemma 3·3, then
![]() $\beta\neq 0$
. Otherwise, the restriction of
$\beta\neq 0$
. Otherwise, the restriction of
![]() $f_{|V(x)}:V(x)\rightarrow \mathbb{C}^3$
of f to the curve
$f_{|V(x)}:V(x)\rightarrow \mathbb{C}^3$
of f to the curve
![]() $V(x) \subset \mathbb{C}^2$
will be generically n-to-1 over its image, a contradiction since f is finitely determined. In this case, we will suppose that
$V(x) \subset \mathbb{C}^2$
will be generically n-to-1 over its image, a contradiction since f is finitely determined. In this case, we will suppose that
![]() $\beta=1$
. Also, if f is finitely determined, then by [
Reference Mond18
, proposition 1·15] we have that
$\beta=1$
. Also, if f is finitely determined, then by [
Reference Mond18
, proposition 1·15] we have that
![]() $D(f)=V(\lambda(x,y))$
, where
$D(f)=V(\lambda(x,y))$
, where
 \begin{equation}\lambda(x,y)=x^{s}y^{v} \cdot \displaystyle \left( { \prod_{i=1}^{r}}(y^a-\alpha_i x^b) \right)\end{equation}
\begin{equation}\lambda(x,y)=x^{s}y^{v} \cdot \displaystyle \left( { \prod_{i=1}^{r}}(y^a-\alpha_i x^b) \right)\end{equation}
![]() $s,v \in \lbrace 0,1 \rbrace$
,
$s,v \in \lbrace 0,1 \rbrace$
,
![]() $\alpha_i \in \mathbb{C}$
,
$\alpha_i \in \mathbb{C}$
,
![]() $\alpha_i\neq 0$
for all
$\alpha_i\neq 0$
for all
![]() $i=1,\ldots,r$
and
$i=1,\ldots,r$
and
![]() $r=(b(n-1)(m-1)-s a - v b)/(ab)$
. In particular,
$r=(b(n-1)(m-1)-s a - v b)/(ab)$
. In particular,
![]() $\lambda$
is a quasi-homogeneous polynomial of type
$\lambda$
is a quasi-homogeneous polynomial of type
![]() $(b(n-1)(m-1);a,b)$
. To prove the main result of this section we will need the following three lemmas.
$(b(n-1)(m-1);a,b)$
. To prove the main result of this section we will need the following three lemmas.
Lemma 3·7.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1=a,d_2,d_3;a,b)$
, with
$(d_1=a,d_2,d_3;a,b)$
, with
![]() $d_2\leq d_3$
, and multiplicity greater than 2. Write f as in Lemma 3·3
, that is, in the form
$d_2\leq d_3$
, and multiplicity greater than 2. Write f as in Lemma 3·3
, that is, in the form
Then:
-
(a) V(x) is an irreducible component of D(f) if and only if
 $gcd(n,m)=2$
. Furthermore, if
$gcd(n,m)=2$
. Furthermore, if
 $s=1$
in (5), then V(x) is a fold component of D(f);
$s=1$
in (5), then V(x) is a fold component of D(f);
-
(b) if V(x) is an irreducible component of D(f), then
 $b=1$
and a is odd;
$b=1$
and a is odd;
-
(c) if
 $v=1$
in (5), then V(y) is an identification component of D(f). Furthermore, if V(y) is an irreducible component of D(f), then
$v=1$
in (5), then V(y) is an identification component of D(f). Furthermore, if V(y) is an irreducible component of D(f), then
 $a=1$
;
$a=1$
; -
(d)
 $D(f)=V(\lambda(x,y))$
, where (6)
$D(f)=V(\lambda(x,y))$
, where (6) \begin{equation}\lambda(x,y)=x^{s} \cdot \displaystyle \left( { \prod_{i=1}^{r}}(y^a-\alpha_i x^b) \right)\end{equation}
\begin{equation}\lambda(x,y)=x^{s} \cdot \displaystyle \left( { \prod_{i=1}^{r}}(y^a-\alpha_i x^b) \right)\end{equation}
![]() $s \in \lbrace 0,1 \rbrace $
,
$s \in \lbrace 0,1 \rbrace $
,
![]() $\alpha_i \in \mathbb{C}$
and
$\alpha_i \in \mathbb{C}$
and
![]() $r=\dfrac{b(n-1)(m-1)- sa}{ab}$
.
$r=\dfrac{b(n-1)(m-1)- sa}{ab}$
.
Proof.
-
(a) If
 $gcd(n,m)=2$
, then the restriction of f to V(x) is generically 2-to-1 and therefore V(x) is a fold component of D(f). On the other hand, suppose that
$gcd(n,m)=2$
, then the restriction of f to V(x) is generically 2-to-1 and therefore V(x) is a fold component of D(f). On the other hand, suppose that
 $V(x) \subset D(f)$
and
$V(x) \subset D(f)$
and
 $gcd(n,m) \neq 2$
. Since f is finitely determined, then we should have that
$gcd(n,m) \neq 2$
. Since f is finitely determined, then we should have that
 $gcd(n,m)=1$
. Therefore, V(x) should be an identification component of D(f). Thus, there exist another irreducible component of D(f) that has the same image by f as V(x). By expression (5), this irreducible component should be either V(y) or
$gcd(n,m)=1$
. Therefore, V(x) should be an identification component of D(f). Thus, there exist another irreducible component of D(f) that has the same image by f as V(x). By expression (5), this irreducible component should be either V(y) or
 $V(y^a-\alpha_i x^b)$
for some i. However, note that
$V(y^a-\alpha_i x^b)$
for some i. However, note that
 $f(V(y)) \neq f(V(x))$
and
$f(V(y)) \neq f(V(x))$
and
 $f(V(y^a-\alpha_i x^b)) \neq f(V(x))$
for all i, which is a contradiction.
$f(V(y^a-\alpha_i x^b)) \neq f(V(x))$
for all i, which is a contradiction. -
(b) By expression (5), we have that
 $D(f)=V(\lambda(x,y))$
, where
$D(f)=V(\lambda(x,y))$
, where
 $\lambda$
is quasi-homogeneous of type
$\lambda$
is quasi-homogeneous of type
 $(b(n-1)(m-1);a,b)$
. Thus we can write
$(b(n-1)(m-1);a,b)$
. Thus we can write \begin{align*}\lambda(x,y)&=a_0y^{(n-1)(m-1)}+a_1x^by^{(n-1)(m-1)-a}+a_2x^{2b}y^{(n-1)(m-1)-2a}+\ldots\\ &\quad+a_kx^{\zeta b}y^{(n-1)(m-1)- \zeta a},\end{align*}
\begin{align*}\lambda(x,y)&=a_0y^{(n-1)(m-1)}+a_1x^by^{(n-1)(m-1)-a}+a_2x^{2b}y^{(n-1)(m-1)-2a}+\ldots\\ &\quad+a_kx^{\zeta b}y^{(n-1)(m-1)- \zeta a},\end{align*}
where
![]() $\zeta$
is the greatest positive integer such that
$\zeta$
is the greatest positive integer such that
![]() $(n-1)(m-1)- \zeta a\geq 0$
.
$(n-1)(m-1)- \zeta a\geq 0$
.
Since
![]() $V(x) \subset D(f)$
, then
$V(x) \subset D(f)$
, then
![]() $a_0=0$
. Since f is finitely determined, then by Theorem 2·5 we have that D(f) is reduced, and therefore
$a_0=0$
. Since f is finitely determined, then by Theorem 2·5 we have that D(f) is reduced, and therefore
![]() $b=1$
and
$b=1$
and
![]() $a_1 \neq 0$
. To see that a should be odd, write f in the form:
$a_1 \neq 0$
. To see that a should be odd, write f in the form:
where
![]() $\eta$
(respectively
$\eta$
(respectively
![]() $\theta$
) is the greatest positive integer such that
$\theta$
) is the greatest positive integer such that
![]() $n-\eta a\geq 1$
(respectively
$n-\eta a\geq 1$
(respectively
![]() $m- \theta a\geq 1$
). By formula (2) in Remark 2·4, we obtain that C(f) is the codimension of the ideal
$m- \theta a\geq 1$
). By formula (2) in Remark 2·4, we obtain that C(f) is the codimension of the ideal
![]() $ I = \displaystyle \left\lt n \cdot y^{n-1}+ x\cdot\dfrac{\partial p}{\partial y}, \ m \cdot y^{m-1}+ x\cdot\dfrac{\partial q}{\partial y} \right\gt $
in
$ I = \displaystyle \left\lt n \cdot y^{n-1}+ x\cdot\dfrac{\partial p}{\partial y}, \ m \cdot y^{m-1}+ x\cdot\dfrac{\partial q}{\partial y} \right\gt $
in
![]() $\mathcal{O}_2$
. We conclude that either
$\mathcal{O}_2$
. We conclude that either
![]() $b_{\eta} \neq 0$
and
$b_{\eta} \neq 0$
and
![]() $n-\eta a=1$
or
$n-\eta a=1$
or
![]() $c_{\theta}\neq 0$
and
$c_{\theta}\neq 0$
and
![]() $m-\theta a=1$
. Otherwise, the codimension of I in
$m-\theta a=1$
. Otherwise, the codimension of I in
![]() $\mathcal{O}_2$
is not finite and hence C(f) is also not finite, which is a contradiction since f is finitely determined. Now, we have that n,m are both even. Since either
$\mathcal{O}_2$
is not finite and hence C(f) is also not finite, which is a contradiction since f is finitely determined. Now, we have that n,m are both even. Since either
![]() $n-\eta a=1$
or
$n-\eta a=1$
or
![]() $m- \theta a=1$
, by parity of n,m and a we conclude that a should be odd.
$m- \theta a=1$
, by parity of n,m and a we conclude that a should be odd.
-
(c) Note that the restriction of f to V(y) is generically 1-to-1. Thus, if
 $V(y) \subset D(f)$
, then it is an identification component of D(f). In this case, there exist another irreducible component of D(f), which is necessarily on the form
$V(y) \subset D(f)$
, then it is an identification component of D(f). In this case, there exist another irreducible component of D(f), which is necessarily on the form
 $V(y^a-\alpha_i x^b)$
, for some i with
$V(y^a-\alpha_i x^b)$
, for some i with
 $\alpha_i \neq 0$
, such that
$\alpha_i \neq 0$
, such that
 $f(V(y))=f(V(y^a-\alpha_ix^b))$
. Set
$f(V(y))=f(V(y^a-\alpha_ix^b))$
. Set
 $\mathscr{C}_{\alpha_i}\,{:\!=}\, V(y^a-\alpha_i x^b)$
and consider a parametrisation
$\mathscr{C}_{\alpha_i}\,{:\!=}\, V(y^a-\alpha_i x^b)$
and consider a parametrisation
 $\varphi_{\alpha_i}: W \rightarrow U $
of
$\varphi_{\alpha_i}: W \rightarrow U $
of
 $\mathscr{C}_{\alpha_i}$
defined by
$\mathscr{C}_{\alpha_i}$
defined by
 $\varphi_{\alpha_i}(u)=(u^a,\rho_i u^b)$
, where W is an open neighbourhood of 0 in
$\varphi_{\alpha_i}(u)=(u^a,\rho_i u^b)$
, where W is an open neighbourhood of 0 in
 $\mathbb{C}$
and
$\mathbb{C}$
and
 $\rho_i \in \mathbb{C}$
is such that
$\rho_i \in \mathbb{C}$
is such that
 $\rho_i^a =\alpha_i$
. Since
$\rho_i^a =\alpha_i$
. Since
 $\mathscr{C}_{\alpha_i}$
is an identification component of D(f), then the mapping
$\mathscr{C}_{\alpha_i}$
is an identification component of D(f), then the mapping
 $\tilde{\varphi}_{\alpha_i}\,{:\!=}\, f\circ \varphi_{\alpha_i}: W \rightarrow V$
, defined by (7)is a parametrisation of
$\tilde{\varphi}_{\alpha_i}\,{:\!=}\, f\circ \varphi_{\alpha_i}: W \rightarrow V$
, defined by (7)is a parametrisation of \begin{equation}\tilde{\varphi}_{\alpha_i}\,{:\!=}\, (u^a,\rho_{1,i} u^{d_2}, \rho_{2,i} u^{d_3}),\end{equation}
\begin{equation}\tilde{\varphi}_{\alpha_i}\,{:\!=}\, (u^a,\rho_{1,i} u^{d_2}, \rho_{2,i} u^{d_3}),\end{equation}
 $f(\mathscr{C}_{\alpha_i})$
, for some
$f(\mathscr{C}_{\alpha_i})$
, for some
 $\rho_{1,i}, \rho_{2,i} \in \mathbb{C}$
. Since
$\rho_{1,i}, \rho_{2,i} \in \mathbb{C}$
. Since
 $f(V(y))=f(V(y^a-\alpha_ix^b))$
, then
$f(V(y))=f(V(y^a-\alpha_ix^b))$
, then
 $\rho_{1,i}=\rho_{2,i}=0$
. Since the restriction of f to
$\rho_{1,i}=\rho_{2,i}=0$
. Since the restriction of f to
 $\mathscr{C}_{\alpha_i}$
is generically 1-to-1, we conclude that
$\mathscr{C}_{\alpha_i}$
is generically 1-to-1, we conclude that
 $a=1$
.
$a=1$
.
-
(d) Suppose that
 $v=1$
in (5). By (c), we have that
$v=1$
in (5). By (c), we have that
 $a=1$
. Thus we can rewrite (5) allowing one of the
$a=1$
. Thus we can rewrite (5) allowing one of the
 $\alpha_i's$
to be zero, when
$\alpha_i's$
to be zero, when
 $a=1$
.
$a=1$
.
Lemma 3·8.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1=a,d_2,d_3;a,b)$
, with
$(d_1=a,d_2,d_3;a,b)$
, with
![]() $d_2\leq d_3$
, and multiplicity greater than 2. Let
$d_2\leq d_3$
, and multiplicity greater than 2. Let
![]() $\theta$
be the largest positive integer such that
$\theta$
be the largest positive integer such that
![]() $m-\theta a \geq 1$
. If
$m-\theta a \geq 1$
. If
![]() $a>bn$
, then
$a>bn$
, then
![]() $\theta=(m-1)/a$
and f can be written in the following form
$\theta=(m-1)/a$
and f can be written in the following form
where
![]() $c_1,\ldots,c_{\theta}\in \mathbb{C}$
and
$c_1,\ldots,c_{\theta}\in \mathbb{C}$
and
![]() $c_{\theta}\neq 0$
.
$c_{\theta}\neq 0$
.
Proof. The proof is similar to the proof of Lemma 3·7(b) observing that if
![]() $m-\theta a>1$
or
$m-\theta a>1$
or
![]() $c_{\theta}=0$
then C(f) is not finite, a contradiction since f is finitely determined.
$c_{\theta}=0$
then C(f) is not finite, a contradiction since f is finitely determined.
The following lemma shows how the Milnor number of an irreducible plane curve with only three characteristic exponents can be calculated.
Lemma 3·9.
Let (X,0) be a germ of irreducible reduced plane curve and suppose that it has only three characteristic exponents, denoted by
![]() $e_0,e_1$
and
$e_0,e_1$
and
![]() $e_2$
. Set
$e_2$
. Set
![]() $e\,{:\!=}\, gcd(e_0,e_1)$
, the greatest common divisor of
$e\,{:\!=}\, gcd(e_0,e_1)$
, the greatest common divisor of
![]() $e_0$
and
$e_0$
and
![]() $e_1$
. Then
$e_1$
. Then
Proof. By [
Reference Campillo3
, proposition 4·3·5] one can express the generators of the semigroup
![]() $\Gamma$
of (X,0) in terms of the characteristic exponents
$\Gamma$
of (X,0) in terms of the characteristic exponents
![]() $e_0$
,
$e_0$
,
![]() $e_1$
and
$e_1$
and
![]() $e_2$
. Since (X,0) is a plane curve, the conductor of the semigroup
$e_2$
. Since (X,0) is a plane curve, the conductor of the semigroup
![]() $\Gamma$
coincides with the Milnor number of (X,0). Now, the proof follows by [
Reference Campillo3
, proposition 4·4·5(iii)].
$\Gamma$
coincides with the Milnor number of (X,0). Now, the proof follows by [
Reference Campillo3
, proposition 4·4·5(iii)].
Now we are able to give a positive answer for Question 1 in the case where the multiplicity of f is greater than two. We do this in the following proposition.
Proposition 3·10.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(d_1=a,d_2,d_3;a,b)$
, with
$(d_1=a,d_2,d_3;a,b)$
, with
![]() $d_2\leq d_3$
, and multiplicity greater than 2. Write f as in Lemma 3·3, that is, in the form
$d_2\leq d_3$
, and multiplicity greater than 2. Write f as in Lemma 3·3, that is, in the form
Set
![]() $c\,{:\!=}\, min \lbrace a,d_2 \rbrace$
and let
$c\,{:\!=}\, min \lbrace a,d_2 \rbrace$
and let
![]() $\gamma$
be the transversal slice of f. Then the characteristic exponents of
$\gamma$
be the transversal slice of f. Then the characteristic exponents of
![]() $\gamma$
are given in terms of
$\gamma$
are given in terms of
![]() $a,b, d_2=bn,$
and
$a,b, d_2=bn,$
and
![]() $d_3=bm$
as follows in Table 1.
$d_3=bm$
as follows in Table 1.
Table 1. Characteristic exponents of the transversal slice of f

Proof. Take a representative
![]() $f\,{:}\,U\rightarrow V$
of f. By Lemma 3·7 (d), we have that
$f\,{:}\,U\rightarrow V$
of f. By Lemma 3·7 (d), we have that
![]() $D(f)=V(\lambda(x,y))$
, where
$D(f)=V(\lambda(x,y))$
, where
![]() $s \in \lbrace 0,1 \rbrace$
,
$s \in \lbrace 0,1 \rbrace$
,
![]() $\alpha_i \in \mathbb{C}$
are all distinct and
$\alpha_i \in \mathbb{C}$
are all distinct and
![]() $r=\dfrac{(d_2-b)(d_3-b)-sab}{ab^2}$
.
$r=\dfrac{(d_2-b)(d_3-b)-sab}{ab^2}$
.
Set
![]() $\mathscr{C}_{\alpha_i}\,{:\!=}\, V(y^a-\alpha_i x^b)$
. As in the proof of Lemma 3·7(c), consider a parametrisation
$\mathscr{C}_{\alpha_i}\,{:\!=}\, V(y^a-\alpha_i x^b)$
. As in the proof of Lemma 3·7(c), consider a parametrisation
![]() $\varphi_{\alpha_i}: W \rightarrow U $
of
$\varphi_{\alpha_i}: W \rightarrow U $
of
![]() $\mathscr{C}_{\alpha_i}$
defined by
$\mathscr{C}_{\alpha_i}$
defined by
![]() $\varphi_{\alpha_i}(u)=(u^a,\rho_i u^b)$
, where W is an open neighbourhood of 0 in
$\varphi_{\alpha_i}(u)=(u^a,\rho_i u^b)$
, where W is an open neighbourhood of 0 in
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() $\rho_i \in \mathbb{C}$
is such that
$\rho_i \in \mathbb{C}$
is such that
![]() $\rho_i^a =\alpha_i$
. So, if
$\rho_i^a =\alpha_i$
. So, if
![]() $\mathscr{C}_{\alpha_i}$
is an identification component of D(f), then the mapping
$\mathscr{C}_{\alpha_i}$
is an identification component of D(f), then the mapping
![]() $\tilde{\varphi}_{\alpha_i}\,{:\!=}\, f\circ \varphi_{\alpha_i}: W \rightarrow V$
, defined by
$\tilde{\varphi}_{\alpha_i}\,{:\!=}\, f\circ \varphi_{\alpha_i}: W \rightarrow V$
, defined by
is a parametrisation of
![]() $f(\mathscr{C}_{\alpha_i})$
, for some
$f(\mathscr{C}_{\alpha_i})$
, for some
![]() $\rho_{1,i}, \rho_{2,i} \in \mathbb{C}$
. On the other hand, if
$\rho_{1,i}, \rho_{2,i} \in \mathbb{C}$
. On the other hand, if
![]() $\mathscr{C}_{\alpha_i}$
is a fold component of D(f), then the mapping
$\mathscr{C}_{\alpha_i}$
is a fold component of D(f), then the mapping
![]() $\varphi_{\alpha_i}': W \rightarrow V$
, defined by
$\varphi_{\alpha_i}': W \rightarrow V$
, defined by
is a parametrisation of
![]() $f(\mathscr{C}_{\alpha_i})$
, for some
$f(\mathscr{C}_{\alpha_i})$
, for some
![]() $\rho_{1,i}', \rho_{2,i}' \in \mathbb{C}$
. Set
$\rho_{1,i}', \rho_{2,i}' \in \mathbb{C}$
. Set
![]() $c\,{:\!=}\, min\lbrace a, d_2 \rbrace$
. Note that if
$c\,{:\!=}\, min\lbrace a, d_2 \rbrace$
. Note that if
![]() $a>d_2$
, then
$a>d_2$
, then
![]() $\rho_{1,i},\rho_{1,i}'\neq 0$
, by Lemma 3·8. In this way, by expressions (8) and (9) we can see that the tangent cone of
$\rho_{1,i},\rho_{1,i}'\neq 0$
, by Lemma 3·8. In this way, by expressions (8) and (9) we can see that the tangent cone of
![]() $f(\mathscr{C}_{\alpha_i})$
is the line with direction given by the vector (1,0,0) if
$f(\mathscr{C}_{\alpha_i})$
is the line with direction given by the vector (1,0,0) if
![]() $a<d_2$
,
$a<d_2$
,
![]() $(1,\rho_{1,i},0)$
or
$(1,\rho_{1,i},0)$
or
![]() $(1,\rho_{1,i}^{'},0)$
if
$(1,\rho_{1,i}^{'},0)$
if
![]() $a=d_2$
and finally (0,1,0) if
$a=d_2$
and finally (0,1,0) if
![]() $a>d_2$
.
$a>d_2$
.
Set
![]() $\mathscr{C}\,{:\!=}\, V(x)$
. If
$\mathscr{C}\,{:\!=}\, V(x)$
. If
![]() $\mathscr{C} \subset D(f)$
, then by Lemma 3·7 (a) we have that it is a fold component of D(f). In this case, the map
$\mathscr{C} \subset D(f)$
, then by Lemma 3·7 (a) we have that it is a fold component of D(f). In this case, the map
![]() $\varphi :W\rightarrow V$
defined by
$\varphi :W\rightarrow V$
defined by
is a parametrisation of
![]() $f(\mathscr{C})$
, and hence its tangent is the line with direction given by the vector (0,1,0).
$f(\mathscr{C})$
, and hence its tangent is the line with direction given by the vector (0,1,0).
We are now able to handle all cases. Let’s show the simplest cases A and C first.
-
Case A: By the considerations above, one can see that in this case the plane
 $H=V(X)$
satisfies the conditions (1),(2) and (3) of Definition 3·1. Hence, the restriction of f to the line
$H=V(X)$
satisfies the conditions (1),(2) and (3) of Definition 3·1. Hence, the restriction of f to the line
 $x=0$
, i.e, the map germ
$x=0$
, i.e, the map germ
 $\varphi(u)=f(0,u)=(0,u^{n},u^{m})$
, is a Puiseux parametrisation for
$\varphi(u)=f(0,u)=(0,u^{n},u^{m})$
, is a Puiseux parametrisation for
 $\gamma$
. Therefore, its characteristic exponents are
$\gamma$
. Therefore, its characteristic exponents are
 $n={d_2}/{b}$
and
$n={d_2}/{b}$
and
 $m={d_3}/{b}$
.
$m={d_3}/{b}$
. -
Case C: By Lemma 3·8 we have that
 $p(x,y)=0$
, and therefore we can write f in the form
$p(x,y)=0$
, and therefore we can write f in the form \begin{align*}f(x,y)=(x,y^n,y^m+c_1x^by^{m-a}+c_2x^{2b}y^{m-2a}+\ldots+c_{\theta}x^{\theta b}y),\end{align*}
\begin{align*}f(x,y)=(x,y^n,y^m+c_1x^by^{m-a}+c_2x^{2b}y^{m-2a}+\ldots+c_{\theta}x^{\theta b}y),\end{align*}
where
![]() $c_{\theta} \neq 0$
and
$c_{\theta} \neq 0$
and
![]() $\theta=(m-1)/a$
. By expressions (8) and (9) we can see that the plane
$\theta=(m-1)/a$
. By expressions (8) and (9) we can see that the plane
![]() $H=V(X)$
is not generic for f since the condition (3) of Definition 3·1 fails, that is, H contains the tangent of
$H=V(X)$
is not generic for f since the condition (3) of Definition 3·1 fails, that is, H contains the tangent of
![]() $f(\mathscr{C}_{\alpha_i})$
for all i. Furthermore, condition (2) also fails if
$f(\mathscr{C}_{\alpha_i})$
for all i. Furthermore, condition (2) also fails if
![]() $gcd(n,m)=2$
. However, after the linear change of coordinates on the target given by
$gcd(n,m)=2$
. However, after the linear change of coordinates on the target given by
![]() $(X,Y,Z)\mapsto (X-Y,Y,Z)$
, we can rewrite f as:
$(X,Y,Z)\mapsto (X-Y,Y,Z)$
, we can rewrite f as:
Now, note that the plane
![]() $H=V(X)$
(in the new system of coordinates) satisfies the conditions (1),(2) and (3) of Definition 3·1. Hence, the map germ
$H=V(X)$
(in the new system of coordinates) satisfies the conditions (1),(2) and (3) of Definition 3·1. Hence, the map germ
![]() $\varphi(u)=f(u^n,u)=(0,u^{n},u^{m}+c_1u^{nb+m-a}+c_2u^{2nb+m-2a}+\ldots+c_{\theta}u^{\theta nb+1})$
is a Puiseux parametrisation for
$\varphi(u)=f(u^n,u)=(0,u^{n},u^{m}+c_1u^{nb+m-a}+c_2u^{2nb+m-2a}+\ldots+c_{\theta}u^{\theta nb+1})$
is a Puiseux parametrisation for
![]() $\gamma$
. Now note that
$\gamma$
. Now note that
Note also that
![]() $gcd(n,\theta nb+1)=1$
, therefore the characteristic exponents of
$gcd(n,\theta nb+1)=1$
, therefore the characteristic exponents of
![]() $\gamma$
are
$\gamma$
are
![]() $n={d_2}/{b}$
and
$n={d_2}/{b}$
and
![]() $\theta nb+1= {(d_3-b)d_2}/{ab}+1$
.
$\theta nb+1= {(d_3-b)d_2}/{ab}+1$
.
Finally, we show the most complicated case.
-
Case B: By Lemma 3·7(a) and (b) we obtain that
 $b=1$
, hence we can write f as
$b=1$
, hence we can write f as \begin{align*}f(x,y)&=(x,y^n+b_1xy^{n-a}+b_2x^{2}y^{n-2a}+\ldots+b_{\eta}x^{\eta}y^{n- \eta a},\\ &\quad y^m+c_1xy^{m-a}+c_2x^{2}y^{m-2a}+\ldots+c_{\theta}x^{\theta }y^{m-\theta a}),\end{align*}
\begin{align*}f(x,y)&=(x,y^n+b_1xy^{n-a}+b_2x^{2}y^{n-2a}+\ldots+b_{\eta}x^{\eta}y^{n- \eta a},\\ &\quad y^m+c_1xy^{m-a}+c_2x^{2}y^{m-2a}+\ldots+c_{\theta}x^{\theta }y^{m-\theta a}),\end{align*}
where
![]() $\eta$
(respectively
$\eta$
(respectively
![]() $\theta$
) is the greatest positive integer such that
$\theta$
) is the greatest positive integer such that
![]() $n- \eta a\geq 1$
(respectively
$n- \eta a\geq 1$
(respectively
![]() $m- \theta a\geq 1$
).
$m- \theta a\geq 1$
).
Note that in this case the plane
![]() $H=V(X)$
fails to be generic for f only because the condition (2) fails, since H contains the image of V(x), which is an irreducible component of D(f) (see Lemma 3·7(a) and expression (10)).
$H=V(X)$
fails to be generic for f only because the condition (2) fails, since H contains the image of V(x), which is an irreducible component of D(f) (see Lemma 3·7(a) and expression (10)).
Consider the one-parameter unfolding
![]() $F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
,
$F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
,
![]() $F=(f_t(x,y),t)$
where
$F=(f_t(x,y),t)$
where
![]() $f_t:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is defined as
$f_t:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
is defined as
Statement. We claim that F is Whitney equisingular (see Definition 4·3).
Proof of the Statement. We have that F is upper, that is, F adds in the i-coordinate function of f only terms of weighted degree greater than or equal to
![]() $d_i$
. Hence, F is topologically trivial by [
Reference Damon5
, theorem 1]. By [
Reference Fernández de Bobadilla and Pe Pereira7
, corollary 40] (see also [
Reference Callejas Bedregal, Houston and Ruas2
, theorem 6·2]) we have that
$d_i$
. Hence, F is topologically trivial by [
Reference Damon5
, theorem 1]. By [
Reference Fernández de Bobadilla and Pe Pereira7
, corollary 40] (see also [
Reference Callejas Bedregal, Houston and Ruas2
, theorem 6·2]) we have that
![]() $\mu(D(f_t),0)$
is constant.
$\mu(D(f_t),0)$
is constant.
Let
![]() $\mathscr{C}_{\alpha_i,t}$
(respectively
$\mathscr{C}_{\alpha_i,t}$
(respectively
![]() $\mathscr{C}_{t}$
) be the deformation of
$\mathscr{C}_{t}$
) be the deformation of
![]() $\mathscr{C}_{\alpha_i}$
(respectively,
$\mathscr{C}_{\alpha_i}$
(respectively,
![]() $\mathscr{C}$
) induced by F. Note that the restriction of
$\mathscr{C}$
) induced by F. Note that the restriction of
![]() $f_t$
to V(x) is generically 2-to-1 for any t. This means that
$f_t$
to V(x) is generically 2-to-1 for any t. This means that
![]() $\mathscr{C}_{t}=V(x)$
for any t, that is, F induces a trivial deformation of
$\mathscr{C}_{t}=V(x)$
for any t, that is, F induces a trivial deformation of
![]() $\mathscr{C}$
, hence
$\mathscr{C}$
, hence
![]() $m(f_t(\mathscr{C}_t))=n/2$
for any t. By expressions (8) and (9) we can see that either
$m(f_t(\mathscr{C}_t))=n/2$
for any t. By expressions (8) and (9) we can see that either
![]() $m(f(\mathscr{C}_{\alpha_i}))=a$
(if
$m(f(\mathscr{C}_{\alpha_i}))=a$
(if
![]() $\mathscr{C}_{\alpha_i}$
is an identification component of D(f)) or
$\mathscr{C}_{\alpha_i}$
is an identification component of D(f)) or
![]() $m(f(\mathscr{C}_{\alpha_i}))=a/2$
(if
$m(f(\mathscr{C}_{\alpha_i}))=a/2$
(if
![]() $\mathscr{C}_{\alpha_i}$
is a fold component of D(f)). Since F is upper we see that the multiplicity of
$\mathscr{C}_{\alpha_i}$
is a fold component of D(f)). Since F is upper we see that the multiplicity of
![]() $f_t(\mathscr{C}_{\alpha_i,t})$
should be constant since F adds only terms with degree greater than or equal to the degrees of the coordinate functions of
$f_t(\mathscr{C}_{\alpha_i,t})$
should be constant since F adds only terms with degree greater than or equal to the degrees of the coordinate functions of
![]() $\tilde{\varphi}_{\alpha_i}$
(and also
$\tilde{\varphi}_{\alpha_i}$
(and also
![]() $\varphi^{'}_{\alpha_i}(u)$
). Therefore, the multiplicity of
$\varphi^{'}_{\alpha_i}(u)$
). Therefore, the multiplicity of
![]() $f_t(D(f_t))$
is constant. By [
Reference Gaffney8
, proposition 8·6 and corollary 8·9] we conclude the F is Whitney equisingular, which proves the statement.
$f_t(D(f_t))$
is constant. By [
Reference Gaffney8
, proposition 8·6 and corollary 8·9] we conclude the F is Whitney equisingular, which proves the statement.
Note that
![]() $H\cap f_t(\mathscr{C})=H \cap C(f_t(\mathscr{C}))=0$
for any
$H\cap f_t(\mathscr{C})=H \cap C(f_t(\mathscr{C}))=0$
for any
![]() $t \neq 0$
, where
$t \neq 0$
, where
![]() $H=V(X)$
as above. Now, note that
$H=V(X)$
as above. Now, note that
![]() $H\cap f_t(\mathscr{C}_{\alpha_{i,t}})= H \cap C(f_t(\mathscr{C}_{\alpha_{i,t}}))=0$
for any t. In fact, since F is Whitney equisingular, F(D(F)) is Whitney equisingular. Hence each family of curves
$H\cap f_t(\mathscr{C}_{\alpha_{i,t}})= H \cap C(f_t(\mathscr{C}_{\alpha_{i,t}}))=0$
for any t. In fact, since F is Whitney equisingular, F(D(F)) is Whitney equisingular. Hence each family of curves
![]() $f_t(\mathscr{C}_{\alpha_{i,t}})$
is Whitney equisingular (see [
Reference Giles Flores, Silva and Snoussi9
, proposition 4·11(b)]). Since
$f_t(\mathscr{C}_{\alpha_{i,t}})$
is Whitney equisingular (see [
Reference Giles Flores, Silva and Snoussi9
, proposition 4·11(b)]). Since
![]() $H\cap f(\mathscr{C}_{\alpha_i})= H \cap C(f(\mathscr{C}_{\alpha_i}))=0$
and
$H\cap f(\mathscr{C}_{\alpha_i})= H \cap C(f(\mathscr{C}_{\alpha_i}))=0$
and
![]() $f_t(\mathscr{C}_{\alpha_{i,t}})$
is Whitney equisingular, we conclude that for any t sufficiently small we should have that
$f_t(\mathscr{C}_{\alpha_{i,t}})$
is Whitney equisingular, we conclude that for any t sufficiently small we should have that
![]() $H\cap f_t(\mathscr{C}_{\alpha_{i,t}})= H \cap C(f_t(\mathscr{C}_{\alpha_{i,t}}))=0$
. Therefore, we conclude that the plane H is generic for
$H\cap f_t(\mathscr{C}_{\alpha_{i,t}})= H \cap C(f_t(\mathscr{C}_{\alpha_{i,t}}))=0$
. Therefore, we conclude that the plane H is generic for
![]() $f_t$
for any
$f_t$
for any
![]() $t\neq 0$
small enough. Now, for
$t\neq 0$
small enough. Now, for
![]() $t \neq 0$
, a parametrisation of the transversal slice
$t \neq 0$
, a parametrisation of the transversal slice
![]() $\gamma_{f_t}$
of
$\gamma_{f_t}$
of
![]() $f_t$
is given by:
$f_t$
is given by:
By Lemma 3·7 (b) we obtain that a is odd. Since n is even and
![]() $a\leq d_2=n$
, we have that
$a\leq d_2=n$
, we have that
![]() $a<n$
. Therefore
$a<n$
. Therefore
and
![]() $gcd(n,m,n+m-a)=1$
.
$gcd(n,m,n+m-a)=1$
.
Set
![]() $\epsilon\,{:\!=}\, 1+b_1tu^{n-a}+\ldots+b_{\eta}t^{\eta}u^{\eta n- \eta a}=(1+A(u))$
which is an invertible element in
$\epsilon\,{:\!=}\, 1+b_1tu^{n-a}+\ldots+b_{\eta}t^{\eta}u^{\eta n- \eta a}=(1+A(u))$
which is an invertible element in
![]() $\mathcal{O}_1 \simeq \mathbb{C}\lbrace u \rbrace$
. By [
Reference Niven21
, theorem 3 and 17] (see also [
Reference Cohen4
, theorem 2·2]) we know that there exist an invertible element
$\mathcal{O}_1 \simeq \mathbb{C}\lbrace u \rbrace$
. By [
Reference Niven21
, theorem 3 and 17] (see also [
Reference Cohen4
, theorem 2·2]) we know that there exist an invertible element
![]() $\xi$
in
$\xi$
in
![]() $\mathcal{O}_1$
such that
$\mathcal{O}_1$
such that
![]() $\xi^{n}=\epsilon$
. We denote
$\xi^{n}=\epsilon$
. We denote
![]() $\epsilon^{1/n}\,{:\!=}\, \xi$
. More precisely, we have that
$\epsilon^{1/n}\,{:\!=}\, \xi$
. More precisely, we have that
 \begin{align*}\epsilon^{1/n}=(1+A(u))^{1/n}= \displaystyle \sum_{j=0}^{\infty} \left(\begin{matrix}{1/n}\\ {j}\end{matrix}\right) A(x)^j = 1+\dfrac{1}{n}A(x)+\dfrac{\frac{1}{n}(\frac{1}{n}-1)}{2!}A(x)^2+\ldots,\end{align*}
\begin{align*}\epsilon^{1/n}=(1+A(u))^{1/n}= \displaystyle \sum_{j=0}^{\infty} \left(\begin{matrix}{1/n}\\ {j}\end{matrix}\right) A(x)^j = 1+\dfrac{1}{n}A(x)+\dfrac{\frac{1}{n}(\frac{1}{n}-1)}{2!}A(x)^2+\ldots,\end{align*}
where
![]() $ \left(\begin{matrix}{1/n}\\ {j}\end{matrix}\right)$
denotes the generalised binomial coefficient. Therefore,
$ \left(\begin{matrix}{1/n}\\ {j}\end{matrix}\right)$
denotes the generalised binomial coefficient. Therefore,
where
![]() $`` \ldots "$
in (12) denotes the terms of degree strictly greater than
$`` \ldots "$
in (12) denotes the terms of degree strictly greater than
![]() $n-a$
.
$n-a$
.
Consider the isomorphism
![]() $\chi:(\mathbb{C},0)\rightarrow (\mathbb{C},0)$
defined by
$\chi:(\mathbb{C},0)\rightarrow (\mathbb{C},0)$
defined by
![]() $\chi(u)=u \cdot (\epsilon^{1/n})^{-1}$
. Note that
$\chi(u)=u \cdot (\epsilon^{1/n})^{-1}$
. Note that
 \begin{equation}\varphi \circ \chi(u)=\! \left( u^n, u^m \left( 1 {-} \dfrac{1}{n}b_1u^{n{-}a}{+}\ldots \right) ^m{+}c_1tu^{n{+}m{-}a} \left( 1 {-} \dfrac{1}{n}b_1u^{n{-}a}{+}\ldots \right)^{n+m-a}{+} \ldots \right)\end{equation}
\begin{equation}\varphi \circ \chi(u)=\! \left( u^n, u^m \left( 1 {-} \dfrac{1}{n}b_1u^{n{-}a}{+}\ldots \right) ^m{+}c_1tu^{n{+}m{-}a} \left( 1 {-} \dfrac{1}{n}b_1u^{n{-}a}{+}\ldots \right)^{n+m-a}{+} \ldots \right)\end{equation}
is a Puiseux parametrisation of
![]() $\gamma_t$
, for
$\gamma_t$
, for
![]() $t\neq 0$
. Note also that m is the smallest power (with a non-zero coefficient) that appears in the second coordinate function of
$t\neq 0$
. Note also that m is the smallest power (with a non-zero coefficient) that appears in the second coordinate function of
![]() $\varphi \circ \chi$
in (13). Since
$\varphi \circ \chi$
in (13). Since
![]() $gcd(n,m)=2$
, we obtain that the characteristic exponents of
$gcd(n,m)=2$
, we obtain that the characteristic exponents of
![]() $\gamma_t$
are n,m and k for some
$\gamma_t$
are n,m and k for some
![]() $k>m$
with
$k>m$
with
![]() $gcd(n,m,k)=1$
. By Lemmas 3·4 and 3·9 we obtain that
$gcd(n,m,k)=1$
. By Lemmas 3·4 and 3·9 we obtain that
Therefore,
![]() $k=n+m-a$
. In particular, either
$k=n+m-a$
. In particular, either
![]() $ b_1 \neq 0$
or
$ b_1 \neq 0$
or
![]() $ c_1 \neq 0$
in (13). Now, since F is Whitney equisingular, by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, theorem 5·3] we have that
$ c_1 \neq 0$
in (13). Now, since F is Whitney equisingular, by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, theorem 5·3] we have that
![]() $ \mu(\gamma_t,0)$
is constant along the parameter space. Hence, the family of plane curves
$ \mu(\gamma_t,0)$
is constant along the parameter space. Hence, the family of plane curves
![]() $\gamma_t$
is topologically trivial. Therefore,
$\gamma_t$
is topologically trivial. Therefore,
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma_t$
,
$\gamma_t$
,
![]() $t \neq 0$
, have the same embedded topological type by [
Reference Buchweitz and Greuel1
, theorem 5·2·2]. Thus we conclude that the characteristic exponents of
$t \neq 0$
, have the same embedded topological type by [
Reference Buchweitz and Greuel1
, theorem 5·2·2]. Thus we conclude that the characteristic exponents of
![]() $\gamma$
are
$\gamma$
are
![]() $n=d_2$
,
$n=d_2$
,
![]() $m=d_3$
and
$m=d_3$
and
![]() $n+m-a=d_2+d_3-a$
.
$n+m-a=d_2+d_3-a$
.
Now we are able to present a proof of Theorem 1·1.
Proof of Theorem 1·1: Except in the case where
![]() $a\leq d_2$
,
$a\leq d_2$
,
![]() $4\leq {d_2}/{b}$
and
$4\leq {d_2}/{b}$
and
![]() $gcd(d_2,d_3)=2$
(corresponding to the Case C of Proposition 3·10), we have that
$gcd(d_2,d_3)=2$
(corresponding to the Case C of Proposition 3·10), we have that
![]() $\gamma$
has only two characteristic exponents, namely,
$\gamma$
has only two characteristic exponents, namely,
![]() $n=d_2/b$
and k, where k is described in each case by Propositions 3·5 and 3·10. By Lemma 3·4 we have that:
$n=d_2/b$
and k, where k is described in each case by Propositions 3·5 and 3·10. By Lemma 3·4 we have that:
This implies that
where
![]() $c=min\lbrace a,d_2 \rbrace$
,
$c=min\lbrace a,d_2 \rbrace$
,
![]() $s=0$
if the restriction of f to the line
$s=0$
if the restriction of f to the line
![]() $x=0$
is generically
$x=0$
is generically
![]() $1-$
to
$1-$
to
![]() $-1$
, or
$-1$
, or
![]() $s=1$
, otherwise.
$s=1$
, otherwise.
Remark 3·11. Note that Theorem 1·1 shows that the answer to Question 1 is in the positive. In fact, we only need to show that the number s is determined by the weights and degrees, at least in the cases where s is fundamental to determine the embedded topological type of the transversal slice of f. To see this, one can check that:
-
(1) If
 $m(f(\mathbb{C}^2))\geq 3$
, then
$m(f(\mathbb{C}^2))\geq 3$
, then
 $s=1$
or
$s=1$
or
 $s=0$
otherwise (see Lemma 3·7(a)).
$s=0$
otherwise (see Lemma 3·7(a)).Now, suppose that
 $m(f(\mathbb{C}^2))=2$
, hence we have that
$m(f(\mathbb{C}^2))=2$
, hence we have that
 $d_3=as+rab$
and
$d_3=as+rab$
and
 $r \cdot a$
is even, where r is describe in Lemma 3·7 (d). Then:
$r \cdot a$
is even, where r is describe in Lemma 3·7 (d). Then: -
(2) if
 $b\neq 1$
, then
$b\neq 1$
, then
 $s=1$
if
$s=1$
if
 $d_3\equiv a (mod \ b)$
or
$d_3\equiv a (mod \ b)$
or
 $s=1$
, otherwise;
$s=1$
, otherwise; -
(3) if
 $b=1$
and a is odd, then
$b=1$
and a is odd, then
 $s=1$
if
$s=1$
if
 $d_3\equiv 1 (mod \ 2)$
or
$d_3\equiv 1 (mod \ 2)$
or
 $s=1$
, otherwise;
$s=1$
, otherwise; -
(4) if
 $b=1$
and a is even, it seems that s may be not determined precisely by a relation between the weight and degrees of f. However, in this case Theorem 1·1 says that the characteristic exponents of
$b=1$
and a is even, it seems that s may be not determined precisely by a relation between the weight and degrees of f. However, in this case Theorem 1·1 says that the characteristic exponents of
 $\gamma$
are:
$\gamma$
are:
Therefore, in this case the embedded topological type of
![]() $\gamma$
does not depends on the value of s. We conclude that in any situation (except situation (4) which does not depend on s) the number s is determined by the weights and degrees of f. For instance, the characteristic exponents of
$\gamma$
does not depends on the value of s. We conclude that in any situation (except situation (4) which does not depend on s) the number s is determined by the weights and degrees of f. For instance, the characteristic exponents of
![]() $\gamma$
for any corank 1, finitely determined, quasi-homogeneous map germ of type
$\gamma$
for any corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(1,4,6; 1,1)$
are 4,6,9, since in this case
$(1,4,6; 1,1)$
are 4,6,9, since in this case
![]() $c=s=1$
in Theorem 1·1.
$c=s=1$
in Theorem 1·1.
We finish this section with an example describing the transversal slice of a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(1,4,6; 1,1)$
.
$(1,4,6; 1,1)$
.
Example 3·12. ([
Reference Ruas and Silva24
, example 5·5]). Consider the map germ
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
defined as
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
defined as
It is a corank 1, finitely determined, quasi-homogeneous map germ of type
![]() $(1,4,6; 1,1)$
. Thus,
$(1,4,6; 1,1)$
. Thus,
![]() $c=1$
and
$c=1$
and
![]() $s=1$
and by Theorem 1·1 we conclude that the characteristic exponents of the transversal slice of f are 4, 6 and 9.
$s=1$
and by Theorem 1·1 we conclude that the characteristic exponents of the transversal slice of f are 4, 6 and 9.
4. Some applications, natural questions and examples
In this section, we present two natural consequences of Theorem 1·1. We also consider some natural questions and provide counterexamples for them. We finish this section presenting examples to illustrate our results. For the computations we have made use of the software Singular [
Reference Decker, Greuel, Pfister and Schönemann6
] and the implementation of Mond–Pellikaan’s algorithm given by Hernandes, Miranda and Peñafort–Sanchis in [
Reference Hernandes, Miranda and Peñafort–Sanchis11
]. Alternatively, the reader can consult [
Reference Silva27
, proposition 4·29] for a description of the presentation matrix of the push-forward module
![]() $f_{\ast}\mathcal{O}_{2}$
over
$f_{\ast}\mathcal{O}_{2}$
over
![]() $\mathcal{O}_3$
for maps germs in the form
$\mathcal{O}_3$
for maps germs in the form
![]() $f(x,y)=(x^k,y^n,h(x,y))$
.
$f(x,y)=(x^k,y^n,h(x,y))$
.
4·1. Some applications
As a direct consequence of Theorem 1·1, we present a necessary condition for a corank 1 finitely determined map germ to be quasi-homogeneous with respect to some system of coordinates.
Corollary 4·1.
Consider a corank 1, finitely determined map germ
![]() $g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
of multiplicity n. Then, the following conditions are necessary for the existence of suitable coordinates in which g is quasi-homogeneous.
$g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
of multiplicity n. Then, the following conditions are necessary for the existence of suitable coordinates in which g is quasi-homogeneous.
The transversal slice
![]() $\gamma_g$
of g has:
$\gamma_g$
of g has:
Condition (a): either two characteristic exponents, namely n and l for some
![]() $l>n$
, or
$l>n$
, or
Condition (b): three characteristic exponents, namely,
![]() $n<m<k$
, with
$n<m<k$
, with
![]() $gcd(n,m)=2$
and
$gcd(n,m)=2$
and
![]() $k=n+m-a$
for some m and a.
$k=n+m-a$
for some m and a.
Proof. It follows directly by Theorem 1·1.
It follows by Saito’s criterion for quasi-homogeneity of isolated hypersurfaces singularities [
Reference Saito25
] that if f is a corank 1 finitely determined map germ, then
![]() $\mu(D(g),0)=\tau((D(g),0)$
, where
$\mu(D(g),0)=\tau((D(g),0)$
, where
![]() $\tau$
denotes the Tjurina number. We remark also that another important necessary condition for the existence of suitable coordinates in which g is quasi-homogeneous is that the image Milnor number
$\tau$
denotes the Tjurina number. We remark also that another important necessary condition for the existence of suitable coordinates in which g is quasi-homogeneous is that the image Milnor number
![]() $\mu_I(g)$
should be equal to the
$\mu_I(g)$
should be equal to the
![]() $\mathcal{A}_e$
-codimension (Mond’s
$\mathcal{A}_e$
-codimension (Mond’s
![]() $\tau \leq \mu$
-type inequality, see for instance [
Reference Mond and Nuño–Ballesteros19
]).
$\tau \leq \mu$
-type inequality, see for instance [
Reference Mond and Nuño–Ballesteros19
]).
Example 4·2. Consider the map germ
![]() $g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
defined by
$g:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
defined by
It is a corank 1 finitely determined map germ. One can check that the transversal slice of g has four characteristic exponents: 8,12,14 and 15. Hence, there is no system of coordinates such that g is quasi-homogeneous.
Using Singular we found that
![]() $\mu(D(g),0)=5978>4575=\tau(D(g),0)$
, which is another way to check that g is not quasi-homogeneous.
$\mu(D(g),0)=5978>4575=\tau(D(g),0)$
, which is another way to check that g is not quasi-homogeneous.
Another consequence of Theorem 1·1, is about Whitney equisingularity of a one-parameter unfolding of f.
Definition 4·3. Given an unfolding
![]() $F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
defined by
$F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
defined by
![]() $F(x,y,t)=(f_t(x,y),t)$
, we assume it is origin preserving, that is,
$F(x,y,t)=(f_t(x,y),t)$
, we assume it is origin preserving, that is,
![]() $f_t(0,0)=(0,0)$
for any t. Hence, we have a 1-parameter family of map germs
$f_t(0,0)=(0,0)$
for any t. Hence, we have a 1-parameter family of map germs
![]() $f_t:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
. We say that F is Whitney equisingular if there is a representative of F which admits a regular stratification so that the parameter axes
$f_t:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
. We say that F is Whitney equisingular if there is a representative of F which admits a regular stratification so that the parameter axes
![]() $S=\lbrace (0,0) \times \mathbb{C} \subset \mathbb{C}^2 \times \mathbb{C}$
and
$S=\lbrace (0,0) \times \mathbb{C} \subset \mathbb{C}^2 \times \mathbb{C}$
and
![]() $T=\lbrace (0,0,0) \rbrace \times \mathbb{C} \subset \mathbb{C}^3 \times \mathbb{C}$
are strata.
$T=\lbrace (0,0,0) \rbrace \times \mathbb{C} \subset \mathbb{C}^3 \times \mathbb{C}$
are strata.
Corollary 4·4.
Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined quasi-homogeneous map germ. Consider an one-parameter unfolding
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 1, finitely determined quasi-homogeneous map germ. Consider an one-parameter unfolding
![]() $F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
,
$F\,{:}\,(\mathbb{C}^2 \times \mathbb{C},0)\rightarrow (\mathbb{C}^3 \times \mathbb{C},0)$
,
![]() $F(x,y,t)=(f_t(x,y),t)$
. Write
$F(x,y,t)=(f_t(x,y),t)$
. Write
![]() $f_t$
as:
$f_t$
as:
If F adds only terms of the same degrees as the degrees of f, that is,
![]() $f_t$
is quasi-homogeneous of the same type as f, then F is Whitney equisingular. In particular,
$f_t$
is quasi-homogeneous of the same type as f, then F is Whitney equisingular. In particular,
![]() $m(f_t(\mathbb{C}^2))$
is constant along the parameter space.
$m(f_t(\mathbb{C}^2))$
is constant along the parameter space.
Proof. By [
Reference Damon5
, theorem 1] we have that F is topologically trivial. Hence, by Theorem 2·5 we have that
![]() $\mu(D(f_t),0)$
is constant. Note that f and
$\mu(D(f_t),0)$
is constant. Note that f and
![]() $f_t$
are quasi-homogeneous of the same type. By Theorem 1·1 we have that the embedded topological type of the transversal slice
$f_t$
are quasi-homogeneous of the same type. By Theorem 1·1 we have that the embedded topological type of the transversal slice
![]() $\gamma_t$
of
$\gamma_t$
of
![]() $f_t$
is the same for any t. Hence,
$f_t$
is the same for any t. Hence,
![]() $\mu(\gamma_t,0)$
is constant and therefore F is Whitney equisingular by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, theorem 5·3].
$\mu(\gamma_t,0)$
is constant and therefore F is Whitney equisingular by [
Reference Marar, Nuño–Ballesteros and Peñafort–Sanchis13
, theorem 5·3].
Remark 4·5.
-
(a) We note that if F adds some term of degree strictly greater than the degrees of f then it is topologically trivial but it may be not Whitney equisingular (see [ Reference Ruas and Silva24 , 5.5]).
-
(b) If g has corank 1 (and it is not necessarily quasi-homogeneous), Marar and Nuño–Ballesteros present in [ Reference Marar and Nuño–Ballesteros12 , corollary 4·7] a characterization of Whitney equisingularity of F in terms of the constancy of the invariants C, T and J along the parameter space. If g is quasi-homogeneous, Mond shows in [ Reference Mond18 ] (for any corank) that the invariants C and T are determined by the weights and degrees of g. The author shows in [ Reference Silva26 , theorem 3·2] that the invariant J is also determined by the weights and degrees of f. Hence, it gives another proof of Corollary 4·4.
4·2. Natural questions and examples
We note that Question 1 also makes sense for quasi-homogeneous finitely determined map germs of corank 2. More precisely, one can consider the following natural question.
Question 2. Let
![]() $f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 2 quasi-homogeneous finitely determined map germ. Is the embedded topological type of the transversal slice
$f\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
be a corank 2 quasi-homogeneous finitely determined map germ. Is the embedded topological type of the transversal slice
![]() $\gamma$
of f determined by the weights and degrees of f?
$\gamma$
of f determined by the weights and degrees of f?
The following example shows that the answer to Question 2 is in the negative.
Example 4·6. Consider the map germs
![]() $g_i:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
, defined by
$g_i:(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$
, defined by
Each
![]() $g_i$
is a homogeneous finitely determined map germ of corank 2, of same type,
$g_i$
is a homogeneous finitely determined map germ of corank 2, of same type,
![]() $(2,3,5;1,1)$
(see [
Reference Peñafort–Sanchis23
, example 16] and [
Reference Ruas and Silva24
, example 5.4]). The transversal slice of
$(2,3,5;1,1)$
(see [
Reference Peñafort–Sanchis23
, example 16] and [
Reference Ruas and Silva24
, example 5.4]). The transversal slice of
![]() $g_1$
and
$g_1$
and
![]() $g_2$
has two branches, which we will denoted by
$g_2$
has two branches, which we will denoted by
![]() $\gamma_{i}^1$
and
$\gamma_{i}^1$
and
![]() $\gamma_{i}^2$
. On the other hand, the transversal slice of
$\gamma_{i}^2$
. On the other hand, the transversal slice of
![]() $g_3$
is an irreducible curve, which will denote by
$g_3$
is an irreducible curve, which will denote by
![]() $\gamma=\gamma_3^1$
.
$\gamma=\gamma_3^1$
.
We recall that topological type of a plane curve determines and is determined by the characteristic exponents of each branch and by the intersection multiplicities of the branches. In this way, Table 2 shows that the embedded topological type of these three transversal slices are distinct.
Table 2. Topological invariants for the transversal slice of
![]() $g_i$
$g_i$

Fixed the weights and degrees of a corank 2 finitely determined map germ f from
![]() $(\mathbb{C}^2,0)$
to
$(\mathbb{C}^2,0)$
to
![]() $(\mathbb{C}^3,0)$
, it seems that there is a finite number of distinct topological types for
$(\mathbb{C}^3,0)$
, it seems that there is a finite number of distinct topological types for
![]() $\gamma$
. We propose the following problem:
$\gamma$
. We propose the following problem:
Problem. Fix the weights and degrees of a corank 2 finitely determined map germ f from
![]() $(\mathbb{C}^2,0)$
to
$(\mathbb{C}^2,0)$
to
![]() $(\mathbb{C}^3,0)$
, determine all possible distinct topological types that the transversal slice of f can have.
$(\mathbb{C}^3,0)$
, determine all possible distinct topological types that the transversal slice of f can have.
Since Theorem 1·1 does not extend to the corank 2 case, one might think that the hypothesis of corank 1 must be a special condition that could be considered in other cases. Thus, another natural question is the following one:
Question 3. Let
![]() $f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^{n+1},0)$
, with
$f\,{:}\,(\mathbb{C}^n,0)\rightarrow (\mathbb{C}^{n+1},0)$
, with
![]() $n\geq 3$
be a corank 1 quasi-homogeneous finitely determined map germ.
$n\geq 3$
be a corank 1 quasi-homogeneous finitely determined map germ.
-
(a) Is the embedded topological type of a generic hyperplane section of f determined by the weights and degrees of f?
-
(b) Is the Corollary 4·1 true in this case? That is, a one-parameter unfolding
 $F=(f_t,t)$
of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular?
$F=(f_t,t)$
of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular?
The following example shows that the answers to Question 3 (a) and Question 3 (b) are in the negative.
Example 4·7. Consider the families of map germs
![]() $f_t:(\mathbb{C}^3,0)\rightarrow (\mathbb{C}^4,0)$
defined by
$f_t:(\mathbb{C}^3,0)\rightarrow (\mathbb{C}^4,0)$
defined by
We have that each
![]() $f_t$
is a corank 1 finitely determined map germ of same type, i.e, the deformation of
$f_t$
is a corank 1 finitely determined map germ of same type, i.e, the deformation of
![]() $f_0$
only adds terms of same weighted degrees. However, this family is not Whitney equisingular ([
Reference Damon5
, example 6.2]). One can check also that the generic hyperplane sections
$f_0$
only adds terms of same weighted degrees. However, this family is not Whitney equisingular ([
Reference Damon5
, example 6.2]). One can check also that the generic hyperplane sections
![]() $\gamma_0$
and
$\gamma_0$
and
![]() $\gamma_t$
have distinct embedded topological types.
$\gamma_t$
have distinct embedded topological types.
We finish this work by presenting in Table 3 the characteristic exponents for the transversal slice
![]() $\gamma$
of each map germ in Mond’s list [
Reference Mond17
, p.378].
$\gamma$
of each map germ in Mond’s list [
Reference Mond17
, p.378].
Table 3. Characteristic exponents for
![]() $\gamma$
of quasi-homogeneous map germs in Mond’s list
$\gamma$
of quasi-homogeneous map germs in Mond’s list

![]() $\ast \ c\neq 0,1/2,1,3/2$
.
$\ast \ c\neq 0,1/2,1,3/2$
.
Remark 4·8. We note that all figures used in this work were created by the author using the software SURFER [ 28 ].
Acknowledgements
The author would like to thank the anonymous referee for all suggestions and comments on this work. The author would also like to thank Juan José Nuño–Ballesteros, João Nivaldo Tomazella and Maria Aparecida Soares Ruas for many helpful conversations. The author acknowledges support by São Paulo Research Foundation (FAPESP), grant 2020/10888-2.