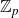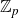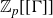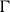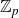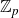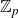1. Introduction
The fine Selmer group has been ever-present in Iwasawa theory. Namely, it has been an object of frequent occurrence in the formulation (and proof) of the Iwasawa main conjecture (see [Reference Kato18, Reference Kobayashi22, Reference Perrin–Riou45, Reference Rubin50]). Despite this, it was only until the turn of the millennium that a systematic study of the said group was first undertook by Coates and Sujatha [Reference Coates and Sujatha3, Reference Coates and Sujatha4], and a little later by Wuthrich [Reference Wuthrich54, Reference Wuthrich55], where they named it as we know today. Initial studies mainly revolved around fine Selmer groups attached to abelian varieties (see loc. cit.; also see [Reference Hachimori12, Reference Kundu and Lim23, Reference Lim and Murty31]). Subsequently, there have been much interest on the fine Selmer group of a modular form (for instance, see [Reference Hatley, Kundu, Lei and Ray14, Reference Jha16, Reference Jha and Sujatha17]) or even more general classes of Galois representations (see [Reference Kleine and Müller21, Reference Lim26, Reference Lim27, Reference Lim and Sujatha32]). A common feature in these cited works is that they are mainly concerned with working over the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension.
$\mathbb{Z}_{p}$
-extension.
Let p be an odd prime. The aim of the paper is to consider the case of a
![]() $\mathbb{Z}_{p}$
-extension which is not the cyclotomic
$\mathbb{Z}_{p}$
-extension which is not the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension. In this context, it has been conjectured that the fine Selmer group should be cotorsion over the ring
$\mathbb{Z}_{p}$
-extension. In this context, it has been conjectured that the fine Selmer group should be cotorsion over the ring
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
, where
$\mathbb{Z}_{p}[[ \Gamma ]]$
, where
![]() $\Gamma$
denotes the Galois group of the
$\Gamma$
denotes the Galois group of the
![]() $\mathbb{Z}_{p}$
-extension (see [Reference Lim28, Reference Perrin–Riou45, Reference Wuthrich54]). This will be called Conjecture Y in the paper. One of our approaches towards studying this conjecture is guided by the following perspective which we now describe. Let
$\mathbb{Z}_{p}$
-extension (see [Reference Lim28, Reference Perrin–Riou45, Reference Wuthrich54]). This will be called Conjecture Y in the paper. One of our approaches towards studying this conjecture is guided by the following perspective which we now describe. Let
![]() $L_\infty$
be a
$L_\infty$
be a
![]() $\mathbb{Z}_{p}^2$
-extension of a number field F, which is assumed to contain
$\mathbb{Z}_{p}^2$
-extension of a number field F, which is assumed to contain
![]() $F^{\textrm{cyc}}$
, the cyclotomic
$F^{\textrm{cyc}}$
, the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension of F. We shall write G for the Galois group
$\mathbb{Z}_{p}$
-extension of F. We shall write G for the Galois group
![]() $\textrm{Gal}(L_\infty/F)$
. Let A be an abelian variety over F. A conjecture of Coates-Sujatha [Reference Coates and Sujatha4, conjecture B] (also see body of this paper) then predicts that the Pontryagin dual of the fine Selmer group, denoted by
$\textrm{Gal}(L_\infty/F)$
. Let A be an abelian variety over F. A conjecture of Coates-Sujatha [Reference Coates and Sujatha4, conjecture B] (also see body of this paper) then predicts that the Pontryagin dual of the fine Selmer group, denoted by
![]() $Y(A/L_\infty)$
, over the
$Y(A/L_\infty)$
, over the
![]() $\mathbb{Z}_{p}^2$
-extension
$\mathbb{Z}_{p}^2$
-extension
![]() $L_\infty$
is pseudo-null over the ring
$L_\infty$
is pseudo-null over the ring
![]() $\mathbb{Z}_{p}[[ G ]]$
. Roughly speaking, this conjecture is saying that
$\mathbb{Z}_{p}[[ G ]]$
. Roughly speaking, this conjecture is saying that
![]() $Y(A/L_\infty)$
is “quite small”. Therefore, in according to this conjecture of Coates–Sujatha, one would expect that the fine Selmer group at each
$Y(A/L_\infty)$
is “quite small”. Therefore, in according to this conjecture of Coates–Sujatha, one would expect that the fine Selmer group at each
![]() $\mathbb{Z}_{p}$
-extension of F contained in
$\mathbb{Z}_{p}$
-extension of F contained in
![]() $L_\infty$
should not be too “large”. More concretely, we have the following observation.
$L_\infty$
should not be too “large”. More concretely, we have the following observation.
Proposition 1·1 (Proposition 3·8). Let A be an abelian variety defined over a number field F, and
![]() $L_{\infty}$
a
$L_{\infty}$
a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Denote by
$F^{\textrm{cyc}}$
. Denote by
![]() $\Phi(L_\infty/F)$
the set of all
$\Phi(L_\infty/F)$
the set of all
![]() $\mathbb{Z}_{p}$
-extensions of F contained in
$\mathbb{Z}_{p}$
-extensions of F contained in
![]() $L_\infty$
. Suppose that
$L_\infty$
. Suppose that
![]() $Y(A/L_\infty)$
is pseudo-null over
$Y(A/L_\infty)$
is pseudo-null over
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(L_\infty/F) ]]$
. Then
$\mathbb{Z}_{p}[[ \textrm{Gal}(L_\infty/F) ]]$
. Then
![]() $Y(A/\mathcal{L})$
is a torsion
$Y(A/\mathcal{L})$
is a torsion
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
$\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
.
$\mathcal{L}\in\Phi(L_\infty/F)$
.
Although there are some numerical examples where pseudo-nullity of
![]() $Y(A/L_\infty)$
has been verified (for instance, see [Reference Jha16, Reference Lei and Palvannan24, Reference Lim27]), the general statement remains wide open. The first of our main result is the following, which gives a way of obtaining infinite classes of
$Y(A/L_\infty)$
has been verified (for instance, see [Reference Jha16, Reference Lei and Palvannan24, Reference Lim27]), the general statement remains wide open. The first of our main result is the following, which gives a way of obtaining infinite classes of
![]() $\mathbb{Z}_{p}$
-extensions, where Conjecture Y is valid.
$\mathbb{Z}_{p}$
-extensions, where Conjecture Y is valid.
Theorem 1·2 (Theorem 3·9). Let A be an abelian variety defined over a number field F, and
![]() $L_{\infty}$
a
$L_{\infty}$
a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Suppose that
$F^{\textrm{cyc}}$
. Suppose that
![]() $Y(A/F^{\textrm{cyc}})$
is torsion over
$Y(A/F^{\textrm{cyc}})$
is torsion over
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
,
$\mathcal{L}\in\Phi(L_\infty/F)$
,
![]() $Y(A/\mathcal{L})$
is torsion over
$Y(A/\mathcal{L})$
is torsion over
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
.
$\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
.
The torsionness of
![]() $Y(A/F^{\textrm{cyc}})$
is known when A is an elliptic curve over
$Y(A/F^{\textrm{cyc}})$
is known when A is an elliptic curve over
![]() $\mathbb{Q}$
and F is an abelian extension of
$\mathbb{Q}$
and F is an abelian extension of
![]() $\mathbb{Q}$
(see [Reference Kato18, Reference Kobayashi22]). Hence the above theorem applies in these cases, where Conjecture Y is valid (also see Section 6 for some examples, where F is not necessarily abelian over
$\mathbb{Q}$
(see [Reference Kato18, Reference Kobayashi22]). Hence the above theorem applies in these cases, where Conjecture Y is valid (also see Section 6 for some examples, where F is not necessarily abelian over
![]() $\mathbb{Q}$
and the theorem applies). This therefore provides a strong evidence to Conjecture Y, and at the same time, a weak partial support towards the pseudo-nullity prediction of Coates–Sujatha.
$\mathbb{Q}$
and the theorem applies). This therefore provides a strong evidence to Conjecture Y, and at the same time, a weak partial support towards the pseudo-nullity prediction of Coates–Sujatha.
As mentioned in the opening paragraph, there has been much interest in the study of the fine Selmer group of a modular form (for instance, see [Reference Hatley, Kundu, Lei and Ray14, Reference Jha16, Reference Jha and Sujatha17]). This will be the next theme of the paper which we describe briefly here.
Let f be a normalised new cuspidal modular eigenform of even weight
![]() $k\geq 2$
, level N and nebentypus
$k\geq 2$
, level N and nebentypus
![]() $\epsilon$
. Write
$\epsilon$
. Write
![]() $A_f$
for the Galois module attached to f (see body of the paper for its precise definition) which is defined over the ring of integers of
$A_f$
for the Galois module attached to f (see body of the paper for its precise definition) which is defined over the ring of integers of
![]() $K_{f,\mathfrak{p}}$
. Here
$K_{f,\mathfrak{p}}$
. Here
![]() $K_f$
is the the number field obtained by adjoining all the Fourier coefficients of f to
$K_f$
is the the number field obtained by adjoining all the Fourier coefficients of f to
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
![]() $K_{f,\mathfrak{p}}$
is the localisation of
$K_{f,\mathfrak{p}}$
is the localisation of
![]() $K_f$
at some fixed prime
$K_f$
at some fixed prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K_f$
above p. Let
$K_f$
above p. Let
![]() $F_{\infty}$
be a
$F_{\infty}$
be a
![]() $\mathbb{Z}_{p}$
-extension of F with
$\mathbb{Z}_{p}$
-extension of F with
![]() $F_n$
being the intermediate subfield satisfying
$F_n$
being the intermediate subfield satisfying
![]() $|F_n:F|=p^n$
. We write
$|F_n:F|=p^n$
. We write
![]() $R(A_f/F_n)$
for the fine Selmer group defined over the field
$R(A_f/F_n)$
for the fine Selmer group defined over the field
![]() $F_n$
for
$F_n$
for
![]() $1\leq n\leq \infty$
, and
$1\leq n\leq \infty$
, and
![]() $Y(A_f/F_n)$
for its Pontryagin dual. We then formulate an analogue of Conjecture Y for
$Y(A_f/F_n)$
for its Pontryagin dual. We then formulate an analogue of Conjecture Y for
![]() $Y(A_f/F_\infty)$
, which will be called Conjecture Y
$Y(A_f/F_\infty)$
, which will be called Conjecture Y
![]() $_f$
(see Conjecture 4·1). Since an analogue of Conjecture B has been postulated and studied by Jha [Reference Jha16], we therefore have a natural analogue of Proposition 3·8 for fine Selmer groups of modular forms (see Proposition 4·3). This in turn inspires the analogue of Theorem 3·9 (see Theorem 4·4). The work of Kato [Reference Kato18] again supplies many classes of examples, where
$_f$
(see Conjecture 4·1). Since an analogue of Conjecture B has been postulated and studied by Jha [Reference Jha16], we therefore have a natural analogue of Proposition 3·8 for fine Selmer groups of modular forms (see Proposition 4·3). This in turn inspires the analogue of Theorem 3·9 (see Theorem 4·4). The work of Kato [Reference Kato18] again supplies many classes of examples, where
![]() $Y(A_f/F^{\textrm{cyc}})$
is torsion, thus allowing one to apply Theorem 4·4 to obtain validity of Conjecture Y
$Y(A_f/F^{\textrm{cyc}})$
is torsion, thus allowing one to apply Theorem 4·4 to obtain validity of Conjecture Y
![]() $_f$
in these cases.
$_f$
in these cases.
We then follow up the above discussion by proving the following control theorem.
Theorem 1·3 (Theorem 4·6). Notations as above. Let S be the set of primes of F containing those dividing pN and the infinite primes. Write
![]() $S_{fd}$
for the set of primes in S which is finitely decomposed in
$S_{fd}$
for the set of primes in S which is finitely decomposed in
![]() $F_\infty/F$
. Suppose further that either of the following statements is valid:
$F_\infty/F$
. Suppose further that either of the following statements is valid:
-
(i) for every prime
 $v\in S_{fd}$
and prime
$v\in S_{fd}$
and prime
 $v_n$
of
$v_n$
of
 $F_n$
above v,
$F_n$
above v,
 $H^0\left(F_{n,v_n}, A_f\right)$
is finite;
$H^0\left(F_{n,v_n}, A_f\right)$
is finite;
-
(ii)
 $K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
$K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
 $H^0(F_v, A_f)$
is finite for every prime
$H^0(F_v, A_f)$
is finite for every prime
 $v\in S_{fd}$
.
$v\in S_{fd}$
.
Then the restriction map
has finite kernel and cokernel which are bounded independently of n.
For an abelian variety, a control theorem of such has been established by the author in [Reference Lim28, theorem 3·3]. The above is therefore an analogue of this in the context of modular forms. Note that in this modular form context, there is an extra finiteness hypothesis on
![]() $H^0(F_v, A_f)$
, and this arises due to a lack of an analogue of Mattuck’s theorem [Reference Mattuck35] for a modular form. We do however remark that although a recent work of Hatley–Kundu–Lei–Ray [Reference Hatley, Kundu, Lei and Ray14] has provided some sufficient conditions for this finiteness hypothesis to hold, it would seem that the general situation seems out of reach at the moment. We also note that in the event that the level N is not divisible by p, then the finiteness is valid for all primes v above p (cf. [Reference Coates, Sujatha and Wintenberger6]).
$H^0(F_v, A_f)$
, and this arises due to a lack of an analogue of Mattuck’s theorem [Reference Mattuck35] for a modular form. We do however remark that although a recent work of Hatley–Kundu–Lei–Ray [Reference Hatley, Kundu, Lei and Ray14] has provided some sufficient conditions for this finiteness hypothesis to hold, it would seem that the general situation seems out of reach at the moment. We also note that in the event that the level N is not divisible by p, then the finiteness is valid for all primes v above p (cf. [Reference Coates, Sujatha and Wintenberger6]).
We say a little more on the finiteness hypothesis on
![]() $H^0(F_v, A_f)$
. As mentioned in the preceding paragraph, this is imposed on us by the lack of an analogue of Mattuck’s theorem. In the proof of the control theorem, since we are estimating the kernel and cokernel at every intermediate
$H^0(F_v, A_f)$
. As mentioned in the preceding paragraph, this is imposed on us by the lack of an analogue of Mattuck’s theorem. In the proof of the control theorem, since we are estimating the kernel and cokernel at every intermediate
![]() $F_n$
, the situation necessitates us to work al prior with a possible stronger hypothesis, namely,
$F_n$
, the situation necessitates us to work al prior with a possible stronger hypothesis, namely,
![]() $H^0\left(F_{n,v_n}, A_f\right)$
is finite for every
$H^0\left(F_{n,v_n}, A_f\right)$
is finite for every
![]() $v_n$
above v. As it turns out, in the event that
$v_n$
above v. As it turns out, in the event that
![]() $K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
, the finiteness hypothesis at the base field suffices. In fact, we shall show that finiteness hypothesis at the base field F will imply the finiteness hypothesis at every intermediate subfield
$K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
, the finiteness hypothesis at the base field suffices. In fact, we shall show that finiteness hypothesis at the base field F will imply the finiteness hypothesis at every intermediate subfield
![]() $F_n$
(see Lemma 4·8 and proof of Theorem 4·6). This latter observation seems interesting in its own right.
$F_n$
(see Lemma 4·8 and proof of Theorem 4·6). This latter observation seems interesting in its own right.
When the modular form arises from a specialization of an ordinary Hida deformation, we attach a fine Selmer group to the Hida deformation (denoted by
![]() $R(\mathcal{A}/F_\infty)$
; whose Pontryagin dual is denoted by
$R(\mathcal{A}/F_\infty)$
; whose Pontryagin dual is denoted by
![]() $Y(\mathcal{A}/F_\infty)$
) and formulate an analogous conjecture which we call Conjecture
$Y(\mathcal{A}/F_\infty)$
) and formulate an analogous conjecture which we call Conjecture
![]() $\mathcal{Y}$
(see Conjecture 5·2). Our main result in this context is the following which can be thought as a “horizontal” variant of Theorems 3·9 and 4·3 (we refer readers to the body of the paper for the definitions of the objects and hypotheses appearing in the theorem).
$\mathcal{Y}$
(see Conjecture 5·2). Our main result in this context is the following which can be thought as a “horizontal” variant of Theorems 3·9 and 4·3 (we refer readers to the body of the paper for the definitions of the objects and hypotheses appearing in the theorem).
Theorem 1·4 (Theorem 5·3). Assume that (H1) and (H2) are valid. Suppose that there exists
![]() $\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
which satisfies the following properties;
$\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
which satisfies the following properties;
-
(a) for every prime
 $v\in S'_{cd}$
, we have
$v\in S'_{cd}$
, we have
 $H^0\left(F_{n,v_n}, A_f\right)$
being finite:
$H^0\left(F_{n,v_n}, A_f\right)$
being finite:
-
(b)
 $R(A_{f_{\eta}}/F_\infty)$
is cotorsion over
$R(A_{f_{\eta}}/F_\infty)$
is cotorsion over
 $\mathcal{O}_\eta[[ \Gamma ]]$
.
$\mathcal{O}_\eta[[ \Gamma ]]$
.
Then Conjecture
![]() $\mathcal{Y}$
is valid, or equivalently,
$\mathcal{Y}$
is valid, or equivalently,
![]() $R(\mathcal{A}/F_\infty)$
is cotorsion over
$R(\mathcal{A}/F_\infty)$
is cotorsion over
![]() $\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
$\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
![]() $R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
$R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
.
$\mathcal{O}_\lambda[[ \Gamma ]]$
.
Note that here again, the lack of an analogue of Mattuck’s theorem necessitates us to work under assumption (a) (for a different set of primes). We should mention that the above theorem is inspired by the work of Jha [Reference Jha16]. Now, looking at Theorems 4·3 and 5·3, one can’t help posing the following question.
Question
![]() $\mathcal{A}$
. Is
$\mathcal{A}$
. Is
![]() $R(\mathcal{A}/F_\infty)^\vee$
pseudo-null over
$R(\mathcal{A}/F_\infty)^\vee$
pseudo-null over
![]() $\mathcal{R}[[ \Gamma ]]$
?
$\mathcal{R}[[ \Gamma ]]$
?
Unfortunately, we do not have an answer to this. In fact, to the best knowledge of the author, even in the context of a cyclotomic
![]() $\mathbb{Z}_{p}$
-extension
$\mathbb{Z}_{p}$
-extension
![]() $F^{\textrm{cyc}}$
, the structure of
$F^{\textrm{cyc}}$
, the structure of
![]() $R(\mathcal{A}/F^{\textrm{cyc}})$
does not seem well-understood (but see a very recent work of Lei-Palvannan [Reference Lei and Palvannan25] for some discussion in this direction).
$R(\mathcal{A}/F^{\textrm{cyc}})$
does not seem well-understood (but see a very recent work of Lei-Palvannan [Reference Lei and Palvannan25] for some discussion in this direction).
It should be evident to the readers that much of the discussion in this paper may be extended to fine Selmer groups attached to even broader classes of Galois representations of interest as studied in [Reference Kleine and Müller21, Reference Lim27, Reference Lim and Sujatha32]. We have decided to restrict our attention to the context of the paper to simplify the presentation. Furthermore, we believe that even in the modular form or Hida deformation context, the occurrence of certain interesting phenomenon deserves further future studies. (For instance, the lack of an analogue of Mattuck’s theorem definitely requires further investigation and this sort of issues will naturally come up if one wants to study fine Selmer groups of more general Galois representations.)
Although the focus of our paper is to formulate variants of Conjecture Y, we should remark that it would be interesting to study the variation of the Iwasawa invariants of the
![]() $\mathbb{Z}_{p}$
-specialisations (either horizontally or vertically). We will not pursue this here but refer readers to [Reference Cuoco7, Reference Greenberg11, Reference Kleine20, Reference Monsky39] for some discussion in the vertical direction. While we have nothing to say about this variational aspect, we shall end by formulating and investigating a generalised Conjecture Y (see Conjecture 7·1) over an arbitrary p-adic Lie extension of dimension
$\mathbb{Z}_{p}$
-specialisations (either horizontally or vertically). We will not pursue this here but refer readers to [Reference Cuoco7, Reference Greenberg11, Reference Kleine20, Reference Monsky39] for some discussion in the vertical direction. While we have nothing to say about this variational aspect, we shall end by formulating and investigating a generalised Conjecture Y (see Conjecture 7·1) over an arbitrary p-adic Lie extension of dimension
![]() $>1$
, and give some conceptual evidences towards the paucity of this generalised conjecture (see Remark 7·2 and Proposition 7·5).
$>1$
, and give some conceptual evidences towards the paucity of this generalised conjecture (see Remark 7·2 and Proposition 7·5).
We now give an outline of our paper. In Section 2, we collect several results on modules over regular local rings which will be required in our arithmetic discussion. In Section 3, we introduce the fine Selmer groups of abelian varieties and establish Theorem 3·9. Section 4 is where we study the fine Selmer group of a modular form. The control theorem for the fine Selmer group of a modular form will be proved in this section. In Section 5, we investigate the relationship between the Conjecture
![]() $\mathcal{Y}$
on the fine Selmer group for a Hida family and the corresponding Conjecture Y
$\mathcal{Y}$
on the fine Selmer group for a Hida family and the corresponding Conjecture Y
![]() $_f$
for the specialisations. We also discuss a situation showing that the conjectural torsionness is consistent with a growth number conjecture of Mazur (see Theorem 5·6). In Section 6, we give several examples to illustrate the results of the paper. Finally, in Section 7, we formulate a generalised Conjecture Y for fine Selmer groups over an arbitrary p-adic Lie extension which does not necessarily contain the cyclotomic
$_f$
for the specialisations. We also discuss a situation showing that the conjectural torsionness is consistent with a growth number conjecture of Mazur (see Theorem 5·6). In Section 6, we give several examples to illustrate the results of the paper. Finally, in Section 7, we formulate a generalised Conjecture Y for fine Selmer groups over an arbitrary p-adic Lie extension which does not necessarily contain the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension. Here we will show that this conjecture is consistent with the pseudo-nullity conjecture of Coates–Sujatha (see Proposition 7·5).
$\mathbb{Z}_{p}$
-extension. Here we will show that this conjecture is consistent with the pseudo-nullity conjecture of Coates–Sujatha (see Proposition 7·5).
2. Review of some commutative algebra
We collect certain commutative algebraic results that will be required for the discussion of the paper. Throughout this section,
![]() $\Lambda$
will always denote a regular local ring. (For our arithmetic purposes, we are usually concerned with regular local rings of the form
$\Lambda$
will always denote a regular local ring. (For our arithmetic purposes, we are usually concerned with regular local rings of the form
![]() $\mathcal{O}[[ T_1, T_2,..., T_r ]]$
, where
$\mathcal{O}[[ T_1, T_2,..., T_r ]]$
, where
![]() $\mathcal{O}$
is some integral domain which is finite flat over
$\mathcal{O}$
is some integral domain which is finite flat over
![]() $\mathbb{Z}_{p}$
.) It’s a standard fact that
$\mathbb{Z}_{p}$
.) It’s a standard fact that
![]() $\Lambda$
is therefore a unique factorisation domain (cf. [Reference Matsumura and Reid34, theorem 20·3]). In particular, it follows from [Reference Matsumura and Reid34, theorem 20·1] that every prime ideal of
$\Lambda$
is therefore a unique factorisation domain (cf. [Reference Matsumura and Reid34, theorem 20·3]). In particular, it follows from [Reference Matsumura and Reid34, theorem 20·1] that every prime ideal of
![]() $\Lambda$
of height one is principal.
$\Lambda$
of height one is principal.
Recall that a finitely generated
![]() $\Lambda$
-module M is said to be torsion if for every element
$\Lambda$
-module M is said to be torsion if for every element
![]() $m\in M$
, there exists
$m\in M$
, there exists
![]() $x\in \Lambda$
such that
$x\in \Lambda$
such that
![]() $x m=0$
. Equivalently, this is saying that
$x m=0$
. Equivalently, this is saying that
![]() $\textrm{Hom}_{\Lambda}(M,\Lambda)=0$
. The module M is said to be pseudo-null if the localisation
$\textrm{Hom}_{\Lambda}(M,\Lambda)=0$
. The module M is said to be pseudo-null if the localisation
![]() $M_{\mathfrak{p}}$
of M at every prime ideal
$M_{\mathfrak{p}}$
of M at every prime ideal
![]() $\mathfrak{p}$
of height
$\mathfrak{p}$
of height
![]() $\leq 1$
is trivial. The latter is equivalent to
$\leq 1$
is trivial. The latter is equivalent to
![]() $\textrm{Ext}_{\Lambda}^i(M,\Lambda)=0$
for
$\textrm{Ext}_{\Lambda}^i(M,\Lambda)=0$
for
![]() $i=0,1$
(for instance, see [Reference Matsumura and Reid34, chapter. 5] or [Reference Neukirch, Schmidt and Wingberg40, chapter. V, section 1]).
$i=0,1$
(for instance, see [Reference Matsumura and Reid34, chapter. 5] or [Reference Neukirch, Schmidt and Wingberg40, chapter. V, section 1]).
We now present a useful lemma (compare with [Reference Perrin-Riou44, section 1·3, lemme 4])
Lemma 2·1.
Let x be an element in
![]() $\Lambda$
which is a generator of a prime ideal of
$\Lambda$
which is a generator of a prime ideal of
![]() $\Lambda$
of height one. Write
$\Lambda$
of height one. Write
![]() $\Omega:=\Lambda/x$
for the quotient ring which is also a regular local ring. Then the following statements are valid:
$\Omega:=\Lambda/x$
for the quotient ring which is also a regular local ring. Then the following statements are valid:
-
(i) if y is another prime element of
 $\Lambda$
which is coprime to x, then
$\Lambda$
which is coprime to x, then
 $\Lambda/(x,y^n)$
is a torsion
$\Lambda/(x,y^n)$
is a torsion
 $\Omega$
-module for every
$\Omega$
-module for every
 $n\geq 1$
;
$n\geq 1$
; -
(ii) if M is a pseudo-null
 $\Lambda$
-module, then both M[x] and
$\Lambda$
-module, then both M[x] and
 $M/x$
are torsion over
$M/x$
are torsion over
 $\Omega$
;
$\Omega$
; -
(iii) if M is a
 $\Lambda$
-module with
$\Lambda$
-module with
 $M/x$
being torsion over
$M/x$
being torsion over
 $\Omega$
, then M is torsion over
$\Omega$
, then M is torsion over
 $\Lambda$
and M[x] is torsion over
$\Lambda$
and M[x] is torsion over
 $\Omega$
.
$\Omega$
.
Proof. We begin proving assertion (i). In fact, we shall establish a slightly stronger assertion: namely, if z is an element of
![]() $\Lambda$
which is coprime to x, then
$\Lambda$
which is coprime to x, then
![]() $\Lambda/(x,z)$
is a torsion
$\Lambda/(x,z)$
is a torsion
![]() $\Omega$
-module. Since z is coprime to x, it does not lie in the ideal (x). Hence
$\Omega$
-module. Since z is coprime to x, it does not lie in the ideal (x). Hence
![]() $z+(x)$
is a nonzero element of
$z+(x)$
is a nonzero element of
![]() $\Omega$
, and it plainly annihilates
$\Omega$
, and it plainly annihilates
![]() $\Lambda/(x,z)$
. Therefore, this proves our first assertion.
$\Lambda/(x,z)$
. Therefore, this proves our first assertion.
For the proof of (ii), we shall write N for either M[x] or
![]() $M/x$
. Since the module N is annihilated by x, it may be viewed as a
$M/x$
. Since the module N is annihilated by x, it may be viewed as a
![]() $\Omega$
-module. Consider the following spectral sequence
$\Omega$
-module. Consider the following spectral sequence
(cf. [Reference Weibel53, exercise 5·6·3]). From the
![]() $\Lambda$
-free resolution
$\Lambda$
-free resolution
of
![]() $\Omega$
, we see that
$\Omega$
, we see that
 \[\textrm{Ext}^j_\Lambda(\Omega, \Lambda)=\left\{ \begin{array}{ll} \Omega, & \quad\mbox{if $j=1$,} \\[5pt] 0, & \quad\hbox{otherwise.} \\ \end{array} \right.\]
\[\textrm{Ext}^j_\Lambda(\Omega, \Lambda)=\left\{ \begin{array}{ll} \Omega, & \quad\mbox{if $j=1$,} \\[5pt] 0, & \quad\hbox{otherwise.} \\ \end{array} \right.\]
Therefore, the spectral sequence (1) degenerates yielding the isomorphism
for
![]() $i\geq 0$
. In particular, we have
$i\geq 0$
. In particular, we have
where the final zero follows from the assumption that M is pseudo-null over
![]() $\Lambda$
. This in turn implies that N is torsion over
$\Lambda$
. This in turn implies that N is torsion over
![]() $\Omega$
and we have the second assertion.
$\Omega$
and we have the second assertion.
The final assertion follows from [Reference Perrin-Riou44, section 1·3, lemme 2] or [Reference Lim27, corollary 4·13].
Now, let M be a finitely generated torsion
![]() $\Lambda$
-module. By [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7], there is a pseudo-isomorphism
$\Lambda$
-module. By [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7], there is a pseudo-isomorphism
where I is a finite indexing set, each
![]() $x_i$
is a generator of a prime ideal of height one and
$x_i$
is a generator of a prime ideal of height one and
![]() $n_i$
is a non-negative integer. Note that the prime ideals
$n_i$
is a non-negative integer. Note that the prime ideals
![]() $\Lambda x_i$
and integers
$\Lambda x_i$
and integers
![]() $n_i$
are determined by the module M.
$n_i$
are determined by the module M.
Lemma 2·2.
Notation as above. Suppose that x is a prime element in
![]() $\Lambda$
which is coprime to all the
$\Lambda$
which is coprime to all the
![]() $x_i$
’s. Then
$x_i$
’s. Then
![]() $M/x$
is a torsion module over the ring
$M/x$
is a torsion module over the ring
![]() $\Omega=\Lambda/x$
.
$\Omega=\Lambda/x$
.
Proof. Let
![]() $P_1=\ker \varphi$
,
$P_1=\ker \varphi$
,
![]() $P_2=\textrm{coker}\,\varphi$
and
$P_2=\textrm{coker}\,\varphi$
and
![]() $Q=\textrm{im}\,\varphi$
, where
$Q=\textrm{im}\,\varphi$
, where
![]() $\varphi$
is given as in (2). From which, we have the following two short exact sequences
$\varphi$
is given as in (2). From which, we have the following two short exact sequences
From which, we have
By Lemma 2·1, the modules
![]() $P_1/x$
,
$P_1/x$
,
![]() $P_2[x]$
and
$P_2[x]$
and
![]() $\bigoplus_{i\in I}\Lambda/(x_i^{n_i},x)$
are torsion over
$\bigoplus_{i\in I}\Lambda/(x_i^{n_i},x)$
are torsion over
![]() $\Omega$
. Putting these observations into the above two exact sequences, we see that so is
$\Omega$
. Putting these observations into the above two exact sequences, we see that so is
![]() $M/x$
.
$M/x$
.
3. Fine Selmer groups of abelian varieties
3·1. Fine Selmer groups
We begin reviewing the fine Selmer groups of abelian varieties following [Reference Coates and Sujatha3, Reference Coates and Sujatha4, Reference Hachimori12, Reference Lim28, Reference Lim and Murty31, Reference Wuthrich54–Reference Wuthrich56]. Fix an odd prime p. Let A be an abelian variety defined over a number field F. Let S be a finite set of primes of F containing the primes above p, the bad reduction primes of A and the infinite primes. Denote by
![]() $F_S$
the maximal algebraic extension of F which is unramified outside S. For every extension
$F_S$
the maximal algebraic extension of F which is unramified outside S. For every extension
![]() $\mathcal{L}$
of F contained in
$\mathcal{L}$
of F contained in
![]() $F_S$
, we write
$F_S$
, we write
![]() $G_S(\mathcal{L})=\textrm{Gal}(F_S/\mathcal{L})$
, and denote by
$G_S(\mathcal{L})=\textrm{Gal}(F_S/\mathcal{L})$
, and denote by
![]() $S(\mathcal{L})$
the set of primes of
$S(\mathcal{L})$
the set of primes of
![]() $\mathcal{L}$
above S.
$\mathcal{L}$
above S.
Let L be a finite extension of F contained in
![]() $F_S$
. The fine Selmer group of A over L is defined by
$F_S$
. The fine Selmer group of A over L is defined by
 \[ R(A/L) =\ker\left(H^1(G_S(L),A[p^{\infty}])\longrightarrow \bigoplus_{v\in S(L)} H^1(L_v, A[p^{\infty}])\right).\]
\[ R(A/L) =\ker\left(H^1(G_S(L),A[p^{\infty}])\longrightarrow \bigoplus_{v\in S(L)} H^1(L_v, A[p^{\infty}])\right).\]
We remark that the above definition is independent of the choice of S (see [Reference Lim and Murty31, lemma 4·1]). Just as the classical p-primary Selmer group, the fine Selmer group sits in the following analogous short exact sequence
where
![]() $\mathcal{M}(A/F)$
is the fine (p-)Mordell–Weil group and
$\mathcal{M}(A/F)$
is the fine (p-)Mordell–Weil group and ![]() is the fine (p-) Tate–Shafarevich group in the sense of Wuthrich [Reference Wuthrich56]. The fine Mordell–Weil group
is the fine (p-) Tate–Shafarevich group in the sense of Wuthrich [Reference Wuthrich56]. The fine Mordell–Weil group
![]() $\mathcal{M}(A/F)$
is defined to be the subgroup of
$\mathcal{M}(A/F)$
is defined to be the subgroup of
![]() $A(F)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}$
consisting of those elements which are mapped to zero in
$A(F)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}$
consisting of those elements which are mapped to zero in
![]() $A(F_v)\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
for all primes v above p. It can be shown that
$A(F_v)\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
for all primes v above p. It can be shown that
![]() $\mathcal{M}(A/F)$
injects into
$\mathcal{M}(A/F)$
injects into
![]() $R(A/F)$
. The fine Tate–Shafarevich group
$R(A/F)$
. The fine Tate–Shafarevich group ![]() is then defined to be the cokernel of this injection (see [Reference Wuthrich56, section 2] for details).
is then defined to be the cokernel of this injection (see [Reference Wuthrich56, section 2] for details).
Let
![]() $F_\infty$
be a (not necessarily cyclotomic)
$F_\infty$
be a (not necessarily cyclotomic)
![]() $\mathbb{Z}_{p}$
-extension of F, whose Galois group
$\mathbb{Z}_{p}$
-extension of F, whose Galois group
![]() $\textrm{Gal}(F_\infty/F)$
will be denoted by
$\textrm{Gal}(F_\infty/F)$
will be denoted by
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $\Gamma_n$
denotes the unique subgroup of
$\Gamma_n$
denotes the unique subgroup of
![]() $\Gamma$
of index
$\Gamma$
of index
![]() $p^n$
, we write
$p^n$
, we write
![]() $F_n$
for the fixed field of
$F_n$
for the fixed field of
![]() $\Gamma_n$
. The fine Selmer group of A over
$\Gamma_n$
. The fine Selmer group of A over
![]() $F_\infty$
is defined to be
$F_\infty$
is defined to be
![]() $R(A/F_\infty) = \displaystyle \mathop{\varinjlim}\limits_n R(A/F_n)$
which comes naturally equipped with a
$R(A/F_\infty) = \displaystyle \mathop{\varinjlim}\limits_n R(A/F_n)$
which comes naturally equipped with a
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
-module structure. The
$\mathbb{Z}_{p}[[ \Gamma ]]$
-module structure. The
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
-modules
$\mathbb{Z}_{p}[[ \Gamma ]]$
-modules
![]() $\mathcal{M}(A/F_\infty)$
and
$\mathcal{M}(A/F_\infty)$
and ![]() are similarly defined by taking limit of the corresponding objects over the intermediate subfields. We shall write
are similarly defined by taking limit of the corresponding objects over the intermediate subfields. We shall write
![]() $Y(A/F_\infty)$
for the Pontryagin dual of
$Y(A/F_\infty)$
for the Pontryagin dual of
![]() $R(A/F_\infty)$
. Upon taking direct limit of the sequence (3) and following up by taking Pontryagin dual, we obtain
$R(A/F_\infty)$
. Upon taking direct limit of the sequence (3) and following up by taking Pontryagin dual, we obtain
It is not difficult to verify that the modules occurring in the exact sequence are finitely generated over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
(for instance, see [Reference Lim28, Lemma 3·2]). In fact, one expects more (see [Reference Lim28, Reference Perrin–Riou45, Reference Wuthrich54]).
$\mathbb{Z}_{p}[[ \Gamma ]]$
(for instance, see [Reference Lim28, Lemma 3·2]). In fact, one expects more (see [Reference Lim28, Reference Perrin–Riou45, Reference Wuthrich54]).
Conjecture 3·1 (Conjecture Y) Let A be an abelian variety defined over a number field F and
![]() $F_\infty$
a
$F_\infty$
a
![]() $\mathbb{Z}_{p}$
-extension of F. Then
$\mathbb{Z}_{p}$
-extension of F. Then
![]() $Y(A/F_\infty)$
is torsion over
$Y(A/F_\infty)$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
.
$\mathbb{Z}_{p}[[ \Gamma ]]$
.
Remark 3·2. (1) When
![]() $F_\infty$
is the cyclotomic
$F_\infty$
is the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension, the above conjecture is a consequence of a conjecture of Mazur [Reference Mazur36] and Schneider [Reference Schneider51] on the structure of the classical Selmer groups. The latter is known when A is an elliptic curve over
$\mathbb{Z}_{p}$
-extension, the above conjecture is a consequence of a conjecture of Mazur [Reference Mazur36] and Schneider [Reference Schneider51] on the structure of the classical Selmer groups. The latter is known when A is an elliptic curve over
![]() $\mathbb{Q}$
with good reduction at p and F is an abelian extension of
$\mathbb{Q}$
with good reduction at p and F is an abelian extension of
![]() $\mathbb{Q}$
(see [Reference Kato18, Reference Kobayashi22]).
$\mathbb{Q}$
(see [Reference Kato18, Reference Kobayashi22]).
(2) Suppose that E is an elliptic curve defined over
![]() $\mathbb{Q}$
with complex multiplication given by a imaginary quadratic field K at which p split completely in
$\mathbb{Q}$
with complex multiplication given by a imaginary quadratic field K at which p split completely in
![]() $K/\mathbb{Q}$
. Let
$K/\mathbb{Q}$
. Let
![]() $K_\infty$
be the
$K_\infty$
be the
![]() $\mathbb{Z}_{p}$
-extension of K which is unramified outside one of the primes of K above p. Then the validity of Conjecture Y is a consequence of a result of Coates (see [Reference de Shalit9, chapter IV, corollary 1·8]; also see the recent papers [Reference Choi, Kezuka and Li1, Reference Kezuka19]).
$\mathbb{Z}_{p}$
-extension of K which is unramified outside one of the primes of K above p. Then the validity of Conjecture Y is a consequence of a result of Coates (see [Reference de Shalit9, chapter IV, corollary 1·8]; also see the recent papers [Reference Choi, Kezuka and Li1, Reference Kezuka19]).
(3) Suppose that E is an elliptic curve defined over
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
![]() $K^{\textrm{ac}}$
the anti-cyclotomic
$K^{\textrm{ac}}$
the anti-cyclotomic
![]() $\mathbb{Z}_{p}$
-extension of an imaginary quadratic field K. Then the
$\mathbb{Z}_{p}$
-extension of an imaginary quadratic field K. Then the
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(K^{\textrm{ac}}/K) ]]$
-torsionness of
$\mathbb{Z}_{p}[[ \textrm{Gal}(K^{\textrm{ac}}/K) ]]$
-torsionness of
![]() $Y(A/K^{\textrm{ac}})$
is known in many cases (for instance, see [Reference Longo and Vigni33, Reference Pollack and Weston47]).
$Y(A/K^{\textrm{ac}})$
is known in many cases (for instance, see [Reference Longo and Vigni33, Reference Pollack and Weston47]).
We record two results taken from [Reference Lim28] which serve as support for Conjecture Y, and will play some role in the subsequent discussion of the paper.
Theorem 3·3.
Let A be an abelian variety defined over a number field F. Let
![]() $F_{\infty}$
be a
$F_{\infty}$
be a
![]() $\mathbb{Z}_{p}$
-extension of F. If
$\mathbb{Z}_{p}$
-extension of F. If
![]() $Y(A/F)$
is finite, then
$Y(A/F)$
is finite, then
![]() $Y(A/F_\infty)$
is torsion over
$Y(A/F_\infty)$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
.
$\mathbb{Z}_{p}[[ \Gamma ]]$
.
Proof. See [Reference Lim28, corollary 3·5].
Proposition 3·4.
Let A be an abelian variety defined over a number field F, and
![]() $F_{\infty}$
a
$F_{\infty}$
a
![]() $\mathbb{Z}_{p}$
-extension of F. Suppose that
$\mathbb{Z}_{p}$
-extension of F. Suppose that ![]() is finite for every n. Then
is finite for every n. Then ![]() is a cotorsion
is a cotorsion
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
-module.
$\mathbb{Z}_{p}[[ \Gamma ]]$
-module.
Proof. See [Reference Lim28, proposition 4·1].
We now record a corollary of the preceding proposition.
Corollary 3·5
Let A be an abelian variety defined over a number field F, and
![]() $F_{\infty}$
a
$F_{\infty}$
a
![]() $\mathbb{Z}_{p}$
-extension of F. Suppose that the following statements are valid.
$\mathbb{Z}_{p}$
-extension of F. Suppose that the following statements are valid.
-
(a)
 is finite for every n.
is finite for every n.
-
(b)
 $A(F_\infty)$
is a finitely generated abelian group.
$A(F_\infty)$
is a finitely generated abelian group.
Then
![]() $Y(A/F_{\infty})$
is a torsion
$Y(A/F_{\infty})$
is a torsion
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
-module.
$\mathbb{Z}_{p}[[ \Gamma ]]$
-module.
Proof. From Proposition 3·4, we see that ![]() is torsion over
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
under hypothesis (a). Hypothesis (b) tells us that
$\mathbb{Z}_{p}[[ \Gamma ]]$
under hypothesis (a). Hypothesis (b) tells us that
![]() $\mathcal{M}(A/F_\infty)^\vee$
is torsion over
$\mathcal{M}(A/F_\infty)^\vee$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
. The conclusion follows from these and the short exact sequence (4).
$\mathbb{Z}_{p}[[ \Gamma ]]$
. The conclusion follows from these and the short exact sequence (4).
3·2. Connection with the pseudo-nullity conjecture of Coates–Sujatha
We now study the relation between our Conjecture Y and the Conjecture B of Coates–Sujatha [Reference Coates and Sujatha4, conjecture B]. As a start, we recall their conjecture, which for now is stated for
![]() $\mathbb{Z}_{p}^2$
-extensions; see Conjecture 7·4 below for the general version.
$\mathbb{Z}_{p}^2$
-extensions; see Conjecture 7·4 below for the general version.
Conjecture 3·6 (Conjecture B). Let
![]() $L_{\infty}$
be a
$L_{\infty}$
be a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Then
$F^{\textrm{cyc}}$
. Then
![]() $Y(A/L_\infty)$
is pseudo-null over
$Y(A/L_\infty)$
is pseudo-null over
![]() $\mathbb{Z}_{p}[[ G ]]$
, where
$\mathbb{Z}_{p}[[ G ]]$
, where
![]() $G=\textrm{Gal}(L_\infty/F)$
.
$G=\textrm{Gal}(L_\infty/F)$
.
Remark 3·7. In [Reference Coates and Sujatha4], they formulated their conjecture under the extra assumption which is their so-called Conjecture A (see [Reference Coates and Sujatha4, conjecture A]). In this paper, we do not require this extra hypothesis, and so the above formulation suffices.
Retaining the above notation, we denote by
![]() $\Phi(L_\infty/F)$
the set of all
$\Phi(L_\infty/F)$
the set of all
![]() $\mathbb{Z}_{p}$
-extensions of F contained in
$\mathbb{Z}_{p}$
-extensions of F contained in
![]() $L_\infty$
. For each
$L_\infty$
. For each
![]() $\mathcal{L}\in \Phi(L_\infty/F)$
, write
$\mathcal{L}\in \Phi(L_\infty/F)$
, write
![]() $\Gamma_{\mathcal{L}}=\textrm{Gal}(\mathcal{L}/F)$
and
$\Gamma_{\mathcal{L}}=\textrm{Gal}(\mathcal{L}/F)$
and
![]() $H_\mathcal{L}=\textrm{Gal}(L_\infty/\mathcal{L})$
. Fix a topological generator
$H_\mathcal{L}=\textrm{Gal}(L_\infty/\mathcal{L})$
. Fix a topological generator
![]() $h_{\mathcal{L}}$
of
$h_{\mathcal{L}}$
of
![]() $H_\mathcal{L}$
. Then
$H_\mathcal{L}$
. Then
![]() $h_{\mathcal{L}}-1$
generates a prime ideal of
$h_{\mathcal{L}}-1$
generates a prime ideal of
![]() $\mathbb{Z}_{p}[[ G ]]$
of height one with
$\mathbb{Z}_{p}[[ G ]]$
of height one with
We can now establish the following observation as mentioned in the introduction.
Proposition 3·8.
Let A be an abelian variety defined over a number field F, and
![]() $L_{\infty}$
a
$L_{\infty}$
a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Suppose that Conjecture B is valid for A over
$F^{\textrm{cyc}}$
. Suppose that Conjecture B is valid for A over
![]() $L_\infty$
, or in other words,
$L_\infty$
, or in other words,
![]() $Y(A/L_\infty)$
is pseudo-null over
$Y(A/L_\infty)$
is pseudo-null over
![]() $\mathbb{Z}_{p}[[ G ]]$
. Then
$\mathbb{Z}_{p}[[ G ]]$
. Then
![]() $Y(A/\mathcal{L})$
is a torsion
$Y(A/\mathcal{L})$
is a torsion
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
$\mathbb{Z}_{p}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
.
$\mathcal{L}\in\Phi(L_\infty/F)$
.
Proof. From the following commutative diagram

we see that
![]() $\ker s$
is contained in
$\ker s$
is contained in
![]() $H^1(H_\mathcal{L},A(L_\infty))$
which is cofinitely generated over
$H^1(H_\mathcal{L},A(L_\infty))$
which is cofinitely generated over
![]() $\mathbb{Z}_{p}$
. Upon taking Pontryagin dual, we obtain a map
$\mathbb{Z}_{p}$
. Upon taking Pontryagin dual, we obtain a map
whose cokernel is finitely generated over
![]() $\mathbb{Z}_{p}$
. Therefore, for a given
$\mathbb{Z}_{p}$
. Therefore, for a given
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
, whenever
$\mathcal{L}\in\Phi(L_\infty/F)$
, whenever
![]() $Y(A/L_\infty)_{H_\mathcal{L}}$
is torsion over
$Y(A/L_\infty)_{H_\mathcal{L}}$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
, so is
$\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
, so is
![]() $Y(A/\mathcal{L})$
.
$Y(A/\mathcal{L})$
.
Now, in view of the hypothesis that
![]() $Y(A/L_\infty)$
is pseudo-null over
$Y(A/L_\infty)$
is pseudo-null over
![]() $\mathbb{Z}_{p}[[ G ]]$
, we may apply Lemma 2·1(ii) to conclude that
$\mathbb{Z}_{p}[[ G ]]$
, we may apply Lemma 2·1(ii) to conclude that
![]() $Y(A/F_\infty)_{H_\mathcal{L}}$
is torsion over
$Y(A/F_\infty)_{H_\mathcal{L}}$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
. Combining this with the assertion in the previous paragraph, we have the conclusion.
$\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
. Combining this with the assertion in the previous paragraph, we have the conclusion.
We now state and prove the following.
Theorem 3·9.
Let A be an abelian variety defined over a number field F, and
![]() $L_{\infty}$
a
$L_{\infty}$
a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Suppose that
$F^{\textrm{cyc}}$
. Suppose that
![]() $Y(A/F^{\textrm{cyc}})$
is torsion over
$Y(A/F^{\textrm{cyc}})$
is torsion over
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
, Conjecture Y is valid for
$\mathcal{L}\in\Phi(L_\infty/F)$
, Conjecture Y is valid for
![]() $Y(A/\mathcal{L})$
or, in other words,
$Y(A/\mathcal{L})$
or, in other words,
![]() $Y(A/\mathcal{L})$
is torsion over
$Y(A/\mathcal{L})$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_\mathcal{L} ]]$
.
$\mathbb{Z}_{p}[[ \Gamma_\mathcal{L} ]]$
.
Proof. By [Reference Lim27, proposition 7·2], it follows from the
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
-torsionness of
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
-torsionness of
![]() $Y(A/F^{\textrm{cyc}})$
that
$Y(A/F^{\textrm{cyc}})$
that
![]() $Y(A/L_\infty)$
is torsion over
$Y(A/L_\infty)$
is torsion over
![]() $\mathbb{Z}_{p}[[ G ]]$
. The structure theorem of
$\mathbb{Z}_{p}[[ G ]]$
. The structure theorem of
![]() $\mathbb{Z}_{p}[[ G ]]$
-modules (cf. [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7]) then implies that there is a pseudo-isomorphism
$\mathbb{Z}_{p}[[ G ]]$
-modules (cf. [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7]) then implies that there is a pseudo-isomorphism
of
![]() $\mathbb{Z}_{p}[[ G ]]$
-modules, where I is some finite indexing set and each
$\mathbb{Z}_{p}[[ G ]]$
-modules, where I is some finite indexing set and each
![]() $Q_i$
is a (principal) prime ideal of
$Q_i$
is a (principal) prime ideal of
![]() $\mathbb{Z}_{p}[[ G ]]$
of height one. Since there are only finitely many
$\mathbb{Z}_{p}[[ G ]]$
of height one. Since there are only finitely many
![]() $Q_i$
’s, the element
$Q_i$
’s, the element
![]() $h_{\mathcal{L}}-1$
is coprime to these
$h_{\mathcal{L}}-1$
is coprime to these
![]() $Q_i$
’s for all but finitely many
$Q_i$
’s for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
. For each of such element
$\mathcal{L}\in\Phi(L_\infty/F)$
. For each of such element
![]() $h_{\mathcal{L}}-1$
, it then follows from Lemma 2·2 that
$h_{\mathcal{L}}-1$
, it then follows from Lemma 2·2 that
![]() $Y(A/L_\infty)_{H_\mathcal{L}}=Y(A/L_\infty)/(h_\mathcal{L}-1)$
is torsion over
$Y(A/L_\infty)_{H_\mathcal{L}}=Y(A/L_\infty)/(h_\mathcal{L}-1)$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
. By a similar argument to that in Proposition 3·8, we see that
$\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
. By a similar argument to that in Proposition 3·8, we see that
![]() $Y(A/\mathcal{L})$
is torsion over
$Y(A/\mathcal{L})$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
for every such
$\mathbb{Z}_{p}[[ \Gamma_{\mathcal{L}} ]]$
for every such
![]() $\mathcal{L}$
. This yields the required conclusion of the theorem.
$\mathcal{L}$
. This yields the required conclusion of the theorem.
We record one case, where we can obtain many cases of validity of Conjecture Y.
Corollary 3·10.
Let E be an elliptic curve defined over
![]() $\mathbb{Q}$
and F a finite abelian extension of
$\mathbb{Q}$
and F a finite abelian extension of
![]() $\mathbb{Q}$
. Let
$\mathbb{Q}$
. Let
![]() $L_{\infty}$
be a
$L_{\infty}$
be a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Then for all but finitely many
$F^{\textrm{cyc}}$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
,
$\mathcal{L}\in\Phi(L_\infty/F)$
,
![]() $Y(E/\mathcal{L})$
is cotorsion over
$Y(E/\mathcal{L})$
is cotorsion over
![]() $\mathbb{Z}_{p}[[ \Gamma_\mathcal{L} ]]$
.
$\mathbb{Z}_{p}[[ \Gamma_\mathcal{L} ]]$
.
Proof. A well-known theorem of Kato [Reference Kato18] (also see [Reference Kobayashi22]) asserts that
![]() $R(E/F^{\textrm{cyc}})$
is cotorsion over
$R(E/F^{\textrm{cyc}})$
is cotorsion over
![]() $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. The corollary is now an immediate consequence of this and Theorem 3·9.
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. The corollary is now an immediate consequence of this and Theorem 3·9.
We also refer readers to Section 6 for examples, where F is not necessarily abelian over
![]() $\mathbb{Q}$
but Theorem 3·9 applies.
$\mathbb{Q}$
but Theorem 3·9 applies.
4. Fine Selmer groups of elliptic modular forms
As before, p will denote a fixed odd prime. Let f be a normalised new cuspidal modular eigenform of even weight
![]() $k\geq 2$
, level N and nebentypus
$k\geq 2$
, level N and nebentypus
![]() $\epsilon$
. Let
$\epsilon$
. Let
![]() $\mathcal{K}_f$
be the number field obtained by adjoining all the Fourier coefficients of f to
$\mathcal{K}_f$
be the number field obtained by adjoining all the Fourier coefficients of f to
![]() $\mathbb{Q}$
. Throughout, we shall fix a prime
$\mathbb{Q}$
. Throughout, we shall fix a prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $\mathcal{K}_f$
above p, and let
$\mathcal{K}_f$
above p, and let
![]() $V_f$
denote the corresponding two-dimensional
$V_f$
denote the corresponding two-dimensional
![]() $\mathcal{K}_{f,\mathfrak{p}}$
-linear Galois representation attached to f in the sense of Deligne [Reference Deligne8]. Writing
$\mathcal{K}_{f,\mathfrak{p}}$
-linear Galois representation attached to f in the sense of Deligne [Reference Deligne8]. Writing
![]() $\mathcal{O}=\mathcal{O}_{\mathcal{K}_{f,\mathfrak{p}}}$
for the ring of integers of
$\mathcal{O}=\mathcal{O}_{\mathcal{K}_{f,\mathfrak{p}}}$
for the ring of integers of
![]() $\mathcal{K}_{f,\mathfrak{p}}$
, we fix a
$\mathcal{K}_{f,\mathfrak{p}}$
, we fix a
![]() $\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$
-stable
$\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$
-stable
![]() $\mathcal{O}$
-lattice
$\mathcal{O}$
-lattice
![]() $T_f$
in
$T_f$
in
![]() $V_f$
. We then set
$V_f$
. We then set
![]() $A_f = V_f/T_f$
. Note that
$A_f = V_f/T_f$
. Note that
![]() $A_f$
is isomorphic to
$A_f$
is isomorphic to
![]() $\mathcal{K}_{f,\mathfrak{p}}/\mathcal{O}\oplus \mathcal{K}_{f,\mathfrak{p}}/\mathcal{O}$
as
$\mathcal{K}_{f,\mathfrak{p}}/\mathcal{O}\oplus \mathcal{K}_{f,\mathfrak{p}}/\mathcal{O}$
as
![]() $\mathcal{O}$
-modules.
$\mathcal{O}$
-modules.
Let F be a finite extension of
![]() $\mathbb{Q}$
. Denote by S a finite set of primes of F containing those dividing pN and all the infinite primes. Let
$\mathbb{Q}$
. Denote by S a finite set of primes of F containing those dividing pN and all the infinite primes. Let
![]() $F_\infty$
be a
$F_\infty$
be a
![]() $\mathbb{Z}_{p}$
-extension of F. Following [Reference Jha16, Reference Jha and Sujatha17], we define the fine Selmer group of
$\mathbb{Z}_{p}$
-extension of F. Following [Reference Jha16, Reference Jha and Sujatha17], we define the fine Selmer group of
![]() $A_f$
over
$A_f$
over
![]() $F_\infty$
to be
$F_\infty$
to be
![]() $\displaystyle \mathop{\varinjlim}\limits_nR(A_f/F_n)$
, where
$\displaystyle \mathop{\varinjlim}\limits_nR(A_f/F_n)$
, where
![]() $F_n$
is the intermediate subfield of
$F_n$
is the intermediate subfield of
![]() $F_\infty/F$
with
$F_\infty/F$
with
![]() $|F_n:F|=p^n$
and
$|F_n:F|=p^n$
and
![]() $R(A_f/F_n)$
is defined by
$R(A_f/F_n)$
is defined by
 \[ R(A_f/F_n) =\ker\left(H^1(G_S(F_n),A_f)\longrightarrow \bigoplus_{v\in S(F_n)} H^1(F_{n,v}, A_f)\right).\]
\[ R(A_f/F_n) =\ker\left(H^1(G_S(F_n),A_f)\longrightarrow \bigoplus_{v\in S(F_n)} H^1(F_{n,v}, A_f)\right).\]
The Pontryagin dual of
![]() $R(A_f/F_\infty)$
is then denoted by
$R(A_f/F_\infty)$
is then denoted by
![]() $Y(A_f/F_\infty)$
. As before, one can similarly show that
$Y(A_f/F_\infty)$
. As before, one can similarly show that
![]() $Y(A_f/F_\infty)$
is finitely generated over
$Y(A_f/F_\infty)$
is finitely generated over
![]() $\mathcal{O}[[ \Gamma ]]$
. The following conjecture is the natural analogue of Conjecture Y for modular forms.
$\mathcal{O}[[ \Gamma ]]$
. The following conjecture is the natural analogue of Conjecture Y for modular forms.
Conjecture 4·1 (Conjecture
![]() $\textrm{Y}_f$
). Let
$\textrm{Y}_f$
). Let
![]() $A_f$
be defined as above, and
$A_f$
be defined as above, and
![]() $F_\infty$
a
$F_\infty$
a
![]() $\mathbb{Z}_{p}$
-extension of a number field F. Denote by
$\mathbb{Z}_{p}$
-extension of a number field F. Denote by
![]() $\Gamma$
the Galois group
$\Gamma$
the Galois group
![]() $\textrm{Gal}(F_\infty/F)$
. Then
$\textrm{Gal}(F_\infty/F)$
. Then
![]() $Y(A_f/F_\infty)$
is torsion over
$Y(A_f/F_\infty)$
is torsion over
![]() $\mathcal{O}[[ \Gamma ]]$
.
$\mathcal{O}[[ \Gamma ]]$
.
We now present natural analogue of Proposition 3·8 and Theorem 3·9 for the fine Selmer group of a modular form. As a start, we recall the following analogue of Conjecture B which was first studied by Jha [Reference Jha16].
Conjecture 4·2. Let
![]() $L_{\infty}$
be a
$L_{\infty}$
be a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Then
$F^{\textrm{cyc}}$
. Then
![]() $Y(A_f/L_\infty)$
is pseudo-null over
$Y(A_f/L_\infty)$
is pseudo-null over
![]() $\mathcal{O}[[ G ]]$
, where
$\mathcal{O}[[ G ]]$
, where
![]() $G=\textrm{Gal}(L_\infty/F)$
.
$G=\textrm{Gal}(L_\infty/F)$
.
As in Section 3, denote by
![]() $\Phi(L_\infty/F)$
the set of all
$\Phi(L_\infty/F)$
the set of all
![]() $\mathbb{Z}_{p}$
-extensions of F contained in
$\mathbb{Z}_{p}$
-extensions of F contained in
![]() $L_\infty$
. For each
$L_\infty$
. For each
![]() $\mathcal{L}\in \Phi(L_\infty/F)$
, write
$\mathcal{L}\in \Phi(L_\infty/F)$
, write
![]() $\Gamma_{\mathcal{L}}=\textrm{Gal}(\mathcal{L}/F)$
and
$\Gamma_{\mathcal{L}}=\textrm{Gal}(\mathcal{L}/F)$
and
![]() $H_\mathcal{L}=\textrm{Gal}(L_\infty/\mathcal{L})$
. From which, a similar argument to that in Proposition 3·8 yields the following.
$H_\mathcal{L}=\textrm{Gal}(L_\infty/\mathcal{L})$
. From which, a similar argument to that in Proposition 3·8 yields the following.
Proposition 4·3
Suppose that
![]() $Y(A_f/L_\infty)$
is pseudo-null over
$Y(A_f/L_\infty)$
is pseudo-null over
![]() $\mathcal{O}[[ G ]]$
. Then
$\mathcal{O}[[ G ]]$
. Then
![]() $Y(A_f/\mathcal{L})$
is a torsion
$Y(A_f/\mathcal{L})$
is a torsion
![]() $\mathcal{O}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
$\mathcal{O}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
-module for every
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
.
$\mathcal{L}\in\Phi(L_\infty/F)$
.
Similarly, we can establish the following by a similar argument to that in Theorem 3·9.
Theorem 4·4
Notations as above. Suppose that
![]() $R(A_f/F^{\textrm{cyc}})$
is cotorsion over
$R(A_f/F^{\textrm{cyc}})$
is cotorsion over
![]() $\mathcal{O}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
$\mathcal{O}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
, Conjecture Y
$\mathcal{L}\in\Phi(L_\infty/F)$
, Conjecture Y
![]() $_f$
is valid for
$_f$
is valid for
![]() $Y(A_f/\mathcal{L})$
.
$Y(A_f/\mathcal{L})$
.
Combining the above with Kato’ result [Reference Kato18], we have the following analogue of Corollary 3·10.
Corollary 4·5.
Suppose that F is an abelian extension of
![]() $\mathbb{Q}$
and
$\mathbb{Q}$
and
![]() $L_{\infty}$
a
$L_{\infty}$
a
![]() $\mathbb{Z}_{p}^2$
-extension of F which contains
$\mathbb{Z}_{p}^2$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Then for all but finitely many
$F^{\textrm{cyc}}$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi(L_\infty/F)$
,
$\mathcal{L}\in\Phi(L_\infty/F)$
,
![]() $Y(E/\mathcal{L})$
is cotorsion over
$Y(E/\mathcal{L})$
is cotorsion over
![]() $\mathcal{O}[[ \Gamma_\mathcal{L} ]]$
.
$\mathcal{O}[[ \Gamma_\mathcal{L} ]]$
.
We end the section by establishing a control theorem for the fine Selmer groups of elliptic modular forms, which is the analogue to that in [Reference Lim28, theorem 3·3] proved for abelian varieties. From now on, we let
![]() $S_{fd}$
denote the set of primes in S which do not split completely in
$S_{fd}$
denote the set of primes in S which do not split completely in
![]() $F_\infty/F$
. We shall also write
$F_\infty/F$
. We shall also write
![]() $W(L) = W^{\textrm{Gal}(F_S/L)}$
for any
$W(L) = W^{\textrm{Gal}(F_S/L)}$
for any
![]() $F \subseteq L \subseteq F_S$
. Similarly, for each
$F \subseteq L \subseteq F_S$
. Similarly, for each
![]() $v \in S$
, we write
$v \in S$
, we write
![]() $W(L) = W^{\textrm{Gal}(\bar{F}_v/L)}$
for any
$W(L) = W^{\textrm{Gal}(\bar{F}_v/L)}$
for any
![]() $F_v \subseteq L \subseteq \bar{F}_v$
.
$F_v \subseteq L \subseteq \bar{F}_v$
.
Theorem 4·6.
Let f be a normalized new cuspidal modular eigenform of even weight
![]() $k\geq 2$
, level N and nebentypus
$k\geq 2$
, level N and nebentypus
![]() $\epsilon$
. Write
$\epsilon$
. Write
![]() $A_f$
for the Galois module attached to f defined as above. Let
$A_f$
for the Galois module attached to f defined as above. Let
![]() $F_{\infty}$
be a
$F_{\infty}$
be a
![]() $\mathbb{Z}_{p}$
-extension of F with
$\mathbb{Z}_{p}$
-extension of F with
![]() $F_n$
being the intermediate subfield satisfying
$F_n$
being the intermediate subfield satisfying
![]() $|F_n\,:\,F|=p^n$
. Suppose that either of the following statements is valid.
$|F_n\,:\,F|=p^n$
. Suppose that either of the following statements is valid.
-
(i) For every prime
 $v\in S_{fd}$
and
$v\in S_{fd}$
and
 $v_n$
of
$v_n$
of
 $F_n$
dividing v, then
$F_n$
dividing v, then
 $H^0\left(F_{n,v_n}, A_f\right)$
is finite.
$H^0\left(F_{n,v_n}, A_f\right)$
is finite.
-
(ii)
 $K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
$K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
 $H^0(F_v, A_f)$
is finite for every prime
$H^0(F_v, A_f)$
is finite for every prime
 $v\in S_{fd}$
.
$v\in S_{fd}$
.
Then the restriction map
has finite kernel and cokernel which are bounded independently of n.
Remark 4·7. In the case when
![]() $p\nmid N$
, one automatically has the finiteness of
$p\nmid N$
, one automatically has the finiteness of
![]() $H^0\left(F_{n,v_n}, A_f\right)$
for every
$H^0\left(F_{n,v_n}, A_f\right)$
for every
![]() $v_n$
above p (see [Reference Coates, Sujatha and Wintenberger6]).
$v_n$
above p (see [Reference Coates, Sujatha and Wintenberger6]).
Before proving Theorem 4·6, we establish the following preliminary lemma.
Lemma 4·8.
Let M be a
![]() $\mathcal{O}[[ \Gamma ]]$
-module which is finitely generated over
$\mathcal{O}[[ \Gamma ]]$
-module which is finitely generated over
![]() $\mathcal{O}$
. Suppose that either of the following statements is valid:
$\mathcal{O}$
. Suppose that either of the following statements is valid:
-
(a)
 $M_{\Gamma_n}$
is finite for every n;
$M_{\Gamma_n}$
is finite for every n;
-
(b)
 $K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
$K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
and
 $M_{\Gamma}$
is finite with
$M_{\Gamma}$
is finite with
 $\textrm{rank}_{\mathcal{O}}(M)<p-1$
.
$\textrm{rank}_{\mathcal{O}}(M)<p-1$
.
Then the homology group
![]() $H_1(\Gamma_n, M)$
is finite with order bounded independently of n.
$H_1(\Gamma_n, M)$
is finite with order bounded independently of n.
Proof. Suppose that hypothesis (a) is valid. Since M is plainly torsion as a
![]() $\mathcal{O}[[ \Gamma_n ]]$
-module, one therefore has
$\mathcal{O}[[ \Gamma_n ]]$
-module, one therefore has
where the second equality follows from [Reference Neukirch, Schmidt and Wingberg40, proposition 5·3·20]. Combining these observations, we see that each
![]() $M^{\Gamma_n}$
is finite. This in turn implies that
$M^{\Gamma_n}$
is finite. This in turn implies that
![]() $M^{\Gamma_n}$
is contained in
$M^{\Gamma_n}$
is contained in
![]() $M[p^\infty]$
. But since M is finitely generated over
$M[p^\infty]$
. But since M is finitely generated over
![]() $\mathcal{O}$
, the latter is finite, and hence we conclude that
$\mathcal{O}$
, the latter is finite, and hence we conclude that
![]() $M^{\Gamma_n}$
is finite with order bounded independently of n. Finally, since
$M^{\Gamma_n}$
is finite with order bounded independently of n. Finally, since
![]() $\Gamma_n\cong \mathbb{Z}_{p}$
, we have the identification
$\Gamma_n\cong \mathbb{Z}_{p}$
, we have the identification
![]() $M^{\Gamma_n}\cong H_1(\Gamma_n,M)$
, thus proving the lemma under the validity of the hypothesis (a).
$M^{\Gamma_n}\cong H_1(\Gamma_n,M)$
, thus proving the lemma under the validity of the hypothesis (a).
Now suppose that hypothesis (b) is valid. Identify
![]() $\mathcal{O}[[ \Gamma ]]$
with
$\mathcal{O}[[ \Gamma ]]$
with
![]() $\mathcal{O}[[ T ]]$
under a choice of generator of
$\mathcal{O}[[ T ]]$
under a choice of generator of
![]() $\Gamma$
. Since
$\Gamma$
. Since
![]() $M_{\Gamma}$
is finite, we see that T has to be coprime to the characteristic polynomial of M. Since
$M_{\Gamma}$
is finite, we see that T has to be coprime to the characteristic polynomial of M. Since
![]() $K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
, every other cyclotomic polynomial is irreducible over
$K_{f,\mathfrak{p}}\cap \mathbb{Q}_{p}(\mu_{p^\infty})=\mathbb{Q}_{p}$
, every other cyclotomic polynomial is irreducible over
![]() $\mathcal{O}[[ T ]]$
. Since such a polynomial has degree
$\mathcal{O}[[ T ]]$
. Since such a polynomial has degree
![]() $\geq p-1$
, it has to be coprime to the characteristic polynomial of M. Consequently,
$\geq p-1$
, it has to be coprime to the characteristic polynomial of M. Consequently,
![]() $M_{\Gamma_n}$
is finite for every n. We are therefore in the situation of hypothesis (a), and so the conclusion follows from the above discussion.
$M_{\Gamma_n}$
is finite for every n. We are therefore in the situation of hypothesis (a), and so the conclusion follows from the above discussion.
We can now give the proof of Theorem 4·6.
Proof of Theorem 4·6. Consider the following commutative diagram

with exact rows. Since
![]() $\Gamma_n$
has p-cohomological dimension 1, the restriction-inflation sequence tells us that
$\Gamma_n$
has p-cohomological dimension 1, the restriction-inflation sequence tells us that
![]() $h_n$
is surjective and that
$h_n$
is surjective and that
![]() $\ker h_n = H^1\big(\Gamma_n, A_f(F_\infty)\big)$
. It therefore remains to show the finiteness and boundness of
$\ker h_n = H^1\big(\Gamma_n, A_f(F_\infty)\big)$
. It therefore remains to show the finiteness and boundness of
![]() $\ker h_n$
and
$\ker h_n$
and
![]() $\ker g_{n}$
.
$\ker g_{n}$
.
We begin by showing the finiteness and boundness of
![]() $\ker g_{n}$
. For each
$\ker g_{n}$
. For each
![]() $v_n\in S(F_n)$
, fix a prime of
$v_n\in S(F_n)$
, fix a prime of
![]() $F_\infty$
above
$F_\infty$
above
![]() $v_n$
which is denoted by
$v_n$
which is denoted by
![]() $w_n$
, and write v for the prime of F below
$w_n$
, and write v for the prime of F below
![]() $v_n$
. Write
$v_n$
. Write
![]() $\Gamma_{w_n}$
for the decomposition group of
$\Gamma_{w_n}$
for the decomposition group of
![]() $w_n$
in
$w_n$
in
![]() $\Gamma$
. By the Shapiro’s lemma and the restriction-inflation sequence, we have
$\Gamma$
. By the Shapiro’s lemma and the restriction-inflation sequence, we have
 \[ \ker\left(\bigoplus_{v_n\in S(F_n)} g_{n,v_n} \right) = \bigoplus_{v_n\in S(F_n)} H^1\left(\Gamma_{w_n}, A_f(F_{\infty,v_n})\right).\]
\[ \ker\left(\bigoplus_{v_n\in S(F_n)} g_{n,v_n} \right) = \bigoplus_{v_n\in S(F_n)} H^1\left(\Gamma_{w_n}, A_f(F_{\infty,v_n})\right).\]
If v is a prime of F below
![]() $w_n$
such that v splits completely in
$w_n$
such that v splits completely in
![]() $F_\infty/F$
, then
$F_\infty/F$
, then
![]() $\Gamma_{w_n}=0$
and so one has
$\Gamma_{w_n}=0$
and so one has
![]() $H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right) =0$
. Thus, it remains to consider the primes
$H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right) =0$
. Thus, it remains to consider the primes
![]() $v\in S$
which do not split completely in
$v\in S$
which do not split completely in
![]() $F_\infty/F$
. Since S is a finite set, the number of such possibly nonzero summands
$F_\infty/F$
. Since S is a finite set, the number of such possibly nonzero summands
![]() $\bigoplus H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right)$
is therefore finite and bounded independently of n. Hence it remains to show that each
$\bigoplus H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right)$
is therefore finite and bounded independently of n. Hence it remains to show that each
![]() $H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right)$
is finite and bounded independently for those primes lying above v which do not decompose completely in
$H^1\left(\Gamma_{w_n}, A_f\left(F_{\infty,w_n}\right)\right)$
is finite and bounded independently for those primes lying above v which do not decompose completely in
![]() $F_\infty/F$
. For this, one just needs to verify that either (a) or (b) of Lemma 4·8 is valid. We note that hypothesis (a) is a direct consequence of hypothesis (i) of the theorem. It remains to show that hypothesis (ii) of our theorem yields (b) of the said lemma. For this, it suffices to show that
$F_\infty/F$
. For this, one just needs to verify that either (a) or (b) of Lemma 4·8 is valid. We note that hypothesis (a) is a direct consequence of hypothesis (i) of the theorem. It remains to show that hypothesis (ii) of our theorem yields (b) of the said lemma. For this, it suffices to show that
![]() $\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)<p-1$
. We first consider the case when v does not divide p. In this setting,
$\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)<p-1$
. We first consider the case when v does not divide p. In this setting,
![]() $F_{\infty,w_n}$
is the cyclotomic
$F_{\infty,w_n}$
is the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension of
$\mathbb{Z}_{p}$
-extension of
![]() $F_v$
which is unramified. Since v divides N,
$F_v$
which is unramified. Since v divides N,
![]() $A_f$
cannot be an unramified
$A_f$
cannot be an unramified
![]() $\textrm{Gal}(\bar{F}_v/F_v)$
-module and so
$\textrm{Gal}(\bar{F}_v/F_v)$
-module and so
![]() $A_f$
cannot be realised over
$A_f$
cannot be realised over
![]() $F_{\infty,w_n}$
. Therefore, we must have
$F_{\infty,w_n}$
. Therefore, we must have
![]() $\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)\leq 1$
. As the prime p is assumed to be odd, this in turn implies that
$\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)\leq 1$
. As the prime p is assumed to be odd, this in turn implies that
![]() $\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)<p-1$
. Now suppose that v divides p. It is well-known that
$\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)<p-1$
. Now suppose that v divides p. It is well-known that
![]() $F_v(A_f)$
is a p-adic Lie extension of
$F_v(A_f)$
is a p-adic Lie extension of
![]() $F_v$
of dimension at least 2 (see [Reference Ribet49]). It follows from this that
$F_v$
of dimension at least 2 (see [Reference Ribet49]). It follows from this that
![]() $A_f$
cannot be realised over
$A_f$
cannot be realised over
![]() $F_{\infty,w_n}$
, and so we have
$F_{\infty,w_n}$
, and so we have
![]() $\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)\leq 1$
.
$\textrm{corank}_{\mathcal{O}}\left(A_f\left(F_{\infty,w_n}\right)\right)\leq 1$
.
We now show that
![]() $\ker h_n = H^1(\Gamma_n, A_f(F_\infty))$
is finite and bounded independent of n. Now since
$\ker h_n = H^1(\Gamma_n, A_f(F_\infty))$
is finite and bounded independent of n. Now since
![]() $F_\infty/F$
is a
$F_\infty/F$
is a
![]() $\mathbb{Z}_{p}$
-extension, it must have at least one prime v above p which is ramified in
$\mathbb{Z}_{p}$
-extension, it must have at least one prime v above p which is ramified in
![]() $F_\infty/F$
. In view of the discussion in the preceding paragraph, we have
$F_\infty/F$
. In view of the discussion in the preceding paragraph, we have
![]() $H^0(F_{n,w},A_f)$
being finite, where w is a prime of
$H^0(F_{n,w},A_f)$
being finite, where w is a prime of
![]() $F_\infty$
above v. This in turn implies that
$F_\infty$
above v. This in turn implies that
![]() $H^0(G_S(F_n), A_f)$
is finite for every n. The desired conclusion is now a consequence of Lemma 4·8.
$H^0(G_S(F_n), A_f)$
is finite for every n. The desired conclusion is now a consequence of Lemma 4·8.
Theorem 4·6 has the following natural corollary.
Corollary 4·9.
Retain the settings of Theorem 4·6. Assume further that
![]() $R(A_f/F)$
is finite. Then
$R(A_f/F)$
is finite. Then
![]() $Y(A_f/F_\infty)$
is torsion over
$Y(A_f/F_\infty)$
is torsion over
![]() $\mathcal{O}[[ \Gamma ]]$
.
$\mathcal{O}[[ \Gamma ]]$
.
5. Hida deformations
Let us briefly introduce certain notion and facts arising from the work of Hida [Reference Hida15]. Denote by
![]() $\Gamma'$
the group of diamond operators for the tower of modular curves
$\Gamma'$
the group of diamond operators for the tower of modular curves
![]() $\{Y_1(p^r)\}$
. There is a natural identification of
$\{Y_1(p^r)\}$
. There is a natural identification of
![]() $\Gamma'$
with
$\Gamma'$
with
![]() $1+p\mathbb{Z}_{p}$
which we denote by
$1+p\mathbb{Z}_{p}$
which we denote by
![]() $\kappa:\Gamma'\stackrel{\sim}{\longrightarrow}1+p\mathbb{Z}_{p}$
. For an integer N coprime to p, we write
$\kappa:\Gamma'\stackrel{\sim}{\longrightarrow}1+p\mathbb{Z}_{p}$
. For an integer N coprime to p, we write
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
for the quotient of the universal ordinary Hecke algebra with conductor N corresponding to an ordinary
$h^{\textrm{ord}}_{\mathcal{F}}$
for the quotient of the universal ordinary Hecke algebra with conductor N corresponding to an ordinary
![]() $\mathbb{Z}_{p}[[ \Gamma' ]]$
-adic eigenform
$\mathbb{Z}_{p}[[ \Gamma' ]]$
-adic eigenform
![]() $\mathcal{F}$
. The ring
$\mathcal{F}$
. The ring
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
is a local integral domain which is finite flat over
$h^{\textrm{ord}}_{\mathcal{F}}$
is a local integral domain which is finite flat over
![]() $\mathbb{Z}_{p}[[ \Gamma' ]]$
. In [Reference Hida15], Hida constructed an irreducible representation
$\mathbb{Z}_{p}[[ \Gamma' ]]$
. In [Reference Hida15], Hida constructed an irreducible representation
which is unramified outside Np, and where
![]() $\mathcal{T}_{\mathcal{F}}$
is a finitely generated torsion-free module of generic rank two over
$\mathcal{T}_{\mathcal{F}}$
is a finitely generated torsion-free module of generic rank two over
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
. We now impose two standing assumptions on the pair
$h^{\textrm{ord}}_{\mathcal{F}}$
. We now impose two standing assumptions on the pair
![]() $\left(\mathcal{T}_{\mathcal{F}}, h^{\textrm{ord}}_{\mathcal{F}}\right)$
.
$\left(\mathcal{T}_{\mathcal{F}}, h^{\textrm{ord}}_{\mathcal{F}}\right)$
.
-
(H1) The ring
 $h^{\textrm{ord}}_{\mathcal{F}}$
is isomorphic to
$h^{\textrm{ord}}_{\mathcal{F}}$
is isomorphic to
 $\mathcal{O}[[ \Gamma' ]]$
for the ring of integers
$\mathcal{O}[[ \Gamma' ]]$
for the ring of integers
 $\mathcal{O}$
of a finite extension of
$\mathcal{O}$
of a finite extension of
 $\mathbb{Q}_{p}$
.
$\mathbb{Q}_{p}$
. -
(H2) Denote by
 $\mathfrak{m}$
the maximal ideal of
$\mathfrak{m}$
the maximal ideal of
 $h^{\textrm{ord}}_{\mathcal{F}}$
. The residual representation
$h^{\textrm{ord}}_{\mathcal{F}}$
. The residual representation
 $\bar{\rho}\longrightarrow \textrm{Aut}_{h^{\textrm{ord}}_{\mathcal{F}}/\mathfrak{m}}(\mathcal{T}_{\mathcal{F}}/\mathfrak{m} \mathcal{T}_{\mathcal{F}})$
is absolutely irreducible as a
$\bar{\rho}\longrightarrow \textrm{Aut}_{h^{\textrm{ord}}_{\mathcal{F}}/\mathfrak{m}}(\mathcal{T}_{\mathcal{F}}/\mathfrak{m} \mathcal{T}_{\mathcal{F}})$
is absolutely irreducible as a
 $\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$
-module.
$\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$
-module.
Under
![]() $\textbf{(H2)}$
, the module
$\textbf{(H2)}$
, the module
![]() $\mathcal{T}_{\mathcal{F}}$
is free over
$\mathcal{T}_{\mathcal{F}}$
is free over
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
(see [Reference Mazur and Tilouine38, section 2, corollary 6]). Let
$h^{\textrm{ord}}_{\mathcal{F}}$
(see [Reference Mazur and Tilouine38, section 2, corollary 6]). Let
![]() $\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
be the set consisting of
$\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
be the set consisting of
![]() $\mathbb{Z}_{p}$
-algebra homomorphism
$\mathbb{Z}_{p}$
-algebra homomorphism
![]() $\lambda:h^{\textrm{ord}}_{\mathcal{F}}\longrightarrow \bar{\mathbb{Q}}_p$
which satisfies the property that there exists an open subgroup U of
$\lambda:h^{\textrm{ord}}_{\mathcal{F}}\longrightarrow \bar{\mathbb{Q}}_p$
which satisfies the property that there exists an open subgroup U of
![]() $\Gamma'$
and a non-negative integer w such that
$\Gamma'$
and a non-negative integer w such that
![]() $\lambda(u) = \kappa^w(u)$
for every
$\lambda(u) = \kappa^w(u)$
for every
![]() $u\in U$
. For each of such
$u\in U$
. For each of such
![]() $\lambda$
, we shall write
$\lambda$
, we shall write
![]() $w_\lambda$
for the integer w appearing the above definition. We also write
$w_\lambda$
for the integer w appearing the above definition. We also write
![]() $P_\lambda$
for the kernel of
$P_\lambda$
for the kernel of
![]() $\lambda$
which is a principal prime ideal of
$\lambda$
which is a principal prime ideal of
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
of height one. In fact, identifying
$h^{\textrm{ord}}_{\mathcal{F}}$
of height one. In fact, identifying
![]() $h^{\textrm{ord}}_{\mathcal{F}}\cong \mathcal{O}[[ T ]]$
(recall that we are assuming
$h^{\textrm{ord}}_{\mathcal{F}}\cong \mathcal{O}[[ T ]]$
(recall that we are assuming
![]() $\textbf{(H1)}$
), the prime ideal
$\textbf{(H1)}$
), the prime ideal
![]() $P_\lambda$
can be viewed as lying above the prime ideal of
$P_\lambda$
can be viewed as lying above the prime ideal of
![]() $\mathbb{Z}_{p}[[ T ]]$
generated by
$\mathbb{Z}_{p}[[ T ]]$
generated by
![]() $(1+p)^{w_\lambda}-(1+T)$
. We shall write
$(1+p)^{w_\lambda}-(1+T)$
. We shall write
![]() $p_\lambda$
for a generator of the prime ideal
$p_\lambda$
for a generator of the prime ideal
![]() $P_\lambda$
.
$P_\lambda$
.
By Hida theory, for each
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
, there exists a normalised cuspidal eigenform
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
, there exists a normalised cuspidal eigenform
![]() $f_{\lambda}$
of weight
$f_{\lambda}$
of weight
![]() $w_\lambda+2$
such that
$w_\lambda+2$
such that
![]() $\mathcal{T}_{\mathcal{F}}/P_\lambda\cong T_{f_{\lambda}}$
, where
$\mathcal{T}_{\mathcal{F}}/P_\lambda\cong T_{f_{\lambda}}$
, where
![]() $T_{f_\lambda}$
is the lattice of the Galois representation attached to
$T_{f_\lambda}$
is the lattice of the Galois representation attached to
![]() $f_{\lambda}$
as in the sense of Deligne. Here
$f_{\lambda}$
as in the sense of Deligne. Here
![]() $T_{f_\lambda}$
is a free
$T_{f_\lambda}$
is a free
![]() $\mathcal{O}_\lambda$
-module of rank two, where
$\mathcal{O}_\lambda$
-module of rank two, where
![]() $\mathcal{O}_{\lambda}= h^{\textrm{ord}}_{\mathcal{F}}/P_{\lambda}$
.
$\mathcal{O}_{\lambda}= h^{\textrm{ord}}_{\mathcal{F}}/P_{\lambda}$
.
From now on, to simplify notation, we sometimes write
![]() $\mathcal{T}$
for
$\mathcal{T}$
for
![]() $\mathcal{T}_{\mathcal{F}}$
and
$\mathcal{T}_{\mathcal{F}}$
and
![]() $\mathcal{R}$
for
$\mathcal{R}$
for
![]() $h^{\textrm{ord}}_{\mathcal{F}}$
. Recall that
$h^{\textrm{ord}}_{\mathcal{F}}$
. Recall that
![]() $\mathcal{R}\cong\mathcal{O}[[ \Gamma' ]]$
by our standing assumption
$\mathcal{R}\cong\mathcal{O}[[ \Gamma' ]]$
by our standing assumption
![]() $\textbf{(H1)}$
. Set
$\textbf{(H1)}$
. Set
![]() $\mathcal{A} = \mathcal{T}\otimes_{\mathcal{R}}(\mathcal{R}^{\vee})$
. The next lemma is left to the reader as an exercise.
$\mathcal{A} = \mathcal{T}\otimes_{\mathcal{R}}(\mathcal{R}^{\vee})$
. The next lemma is left to the reader as an exercise.
Lemma 5·1.
One has
![]() $\mathcal{A}[p_\lambda] \cong A_{f_\lambda}$
, where
$\mathcal{A}[p_\lambda] \cong A_{f_\lambda}$
, where
![]() $A_{f_\lambda}$
is the Galois module attached to
$A_{f_\lambda}$
is the Galois module attached to
![]() $f_\lambda$
as in Section 4.
$f_\lambda$
as in Section 4.
Let F be a finite extension of
![]() $\mathbb{Q}$
. Denote by S a finite set of primes of F containing those dividing pN and all the infinite primes. For a
$\mathbb{Q}$
. Denote by S a finite set of primes of F containing those dividing pN and all the infinite primes. For a
![]() $\mathbb{Z}_{p}$
-extension
$\mathbb{Z}_{p}$
-extension
![]() $F_\infty$
of F, the fine Selmer group
$F_\infty$
of F, the fine Selmer group
![]() $R(\mathcal{A}/F_\infty)$
of
$R(\mathcal{A}/F_\infty)$
of
![]() $\mathcal{A}$
over
$\mathcal{A}$
over
![]() $F_\infty$
is defined to be
$F_\infty$
is defined to be
![]() $\displaystyle \mathop{\varinjlim}\limits_n R(\mathcal{A}/F_n)$
, where
$\displaystyle \mathop{\varinjlim}\limits_n R(\mathcal{A}/F_n)$
, where
![]() $F_n$
is the intermediate subfield of
$F_n$
is the intermediate subfield of
![]() $F_\infty/F$
with
$F_\infty/F$
with
![]() $|F_n:F|=p^n$
and
$|F_n:F|=p^n$
and
![]() $R(\mathcal{A}/F_n)$
is given by
$R(\mathcal{A}/F_n)$
is given by
 \[ R(\mathcal{A}/F_n) =\ker\left(H^1(G_S(F_n),\mathcal{A})\longrightarrow \bigoplus_{v_n\in S(F_n)} H^1(F_{n,v_n}, \mathcal{A})\right).\]
\[ R(\mathcal{A}/F_n) =\ker\left(H^1(G_S(F_n),\mathcal{A})\longrightarrow \bigoplus_{v_n\in S(F_n)} H^1(F_{n,v_n}, \mathcal{A})\right).\]
We can now state the following analogue of Conjecture Y for
![]() $\mathcal{A}$
.
$\mathcal{A}$
.
Conjecture 5·2 (Conjecture
![]() $\mathcal{Y}$
) Retain settings as above. Denote by
$\mathcal{Y}$
) Retain settings as above. Denote by
![]() $Y(\mathcal{A}/F_\infty)$
the Pontryagin dual of
$Y(\mathcal{A}/F_\infty)$
the Pontryagin dual of
![]() $R(\mathcal{A}/F_\infty)$
. Then
$R(\mathcal{A}/F_\infty)$
. Then
![]() $Y(\mathcal{A}/F_\infty)$
is torsion over
$Y(\mathcal{A}/F_\infty)$
is torsion over
![]() $\mathcal{R}[[ \Gamma ]]$
, where
$\mathcal{R}[[ \Gamma ]]$
, where
![]() $\Gamma=\textrm{Gal}(F_\infty/F)$
.
$\Gamma=\textrm{Gal}(F_\infty/F)$
.
We now prove a “hortizontal” analogue of Theorems 3·9 and 4·4. In the subsequent discussion, we write
![]() $S'_{cd}$
for the set of primes of S which does not divide p and split completely in
$S'_{cd}$
for the set of primes of S which does not divide p and split completely in
![]() $F_\infty/F$
.
$F_\infty/F$
.
Theorem 5·3.
Assume that (H1) and (H2) are valid. Suppose that there exists
![]() $\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
which satisfies all of the following properties:
$\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
which satisfies all of the following properties:
-
(a) for every prime
 $v\in S'_{cd}$
, the group
$v\in S'_{cd}$
, the group
 $H^0(F_v, A_{f_{\eta}})$
is finite;
$H^0(F_v, A_{f_{\eta}})$
is finite;
-
(b)
 $Y(A_{f_{\eta}}/F_\infty)$
is torsion over
$Y(A_{f_{\eta}}/F_\infty)$
is torsion over
 $\mathcal{O}_\eta[[ \Gamma ]]$
.
$\mathcal{O}_\eta[[ \Gamma ]]$
.
Then Conjecture
![]() $\mathcal{Y}$
is valid, or equivalently,
$\mathcal{Y}$
is valid, or equivalently,
![]() $Y(\mathcal{A}/F_\infty)$
is torsion over
$Y(\mathcal{A}/F_\infty)$
is torsion over
![]() $\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
$\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
![]() $Y\left(A_{f_{\lambda}}/F_\infty\right)$
is torsion over
$Y\left(A_{f_{\lambda}}/F_\infty\right)$
is torsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
.
$\mathcal{O}_\lambda[[ \Gamma ]]$
.
Proof. Consider the following commutative diagram

with exact rows and vertical maps induced by the following short exact sequence
We shall first show that the kernel and cokernel of
![]() $r_\eta$
are cotorsion over
$r_\eta$
are cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
. To start off, we see that
$\mathcal{O}_\eta[[ \Gamma ]]$
. To start off, we see that
![]() $h_\eta$
is surjective with
$h_\eta$
is surjective with
![]() $\ker h_\eta = \mathcal{A}(F_\infty)/P_\eta$
. Since
$\ker h_\eta = \mathcal{A}(F_\infty)/P_\eta$
. Since
![]() $\mathcal{A}(F_\infty)/P_\eta$
is cofinitely generated over
$\mathcal{A}(F_\infty)/P_\eta$
is cofinitely generated over
![]() $\mathcal{O}_\eta$
, it is cotorsion over
$\mathcal{O}_\eta$
, it is cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
. It therefore remains to show that
$\mathcal{O}_\eta[[ \Gamma ]]$
. It therefore remains to show that
![]() $\ker l$
is cotorsion over
$\ker l$
is cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
. For this, we decompose
$\mathcal{O}_\eta[[ \Gamma ]]$
. For this, we decompose
![]() $l=\oplus_{w\in S(F_\infty)}l_w =\oplus_{v\in S}(\oplus_{w|v}l_w)$
and show that
$l=\oplus_{w\in S(F_\infty)}l_w =\oplus_{v\in S}(\oplus_{w|v}l_w)$
and show that
![]() $\ker\big(\oplus_{w|v}l_w\big)$
is cotorsion over
$\ker\big(\oplus_{w|v}l_w\big)$
is cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
for each
$\mathcal{O}_\eta[[ \Gamma ]]$
for each
![]() $v\in S$
. For each w, we have
$v\in S$
. For each w, we have
![]() $\ker l_w = \mathcal{A}(F_{\infty,w})/P_\eta$
. Now if v is finitely decomposed in
$\ker l_w = \mathcal{A}(F_{\infty,w})/P_\eta$
. Now if v is finitely decomposed in
![]() $F_\infty$
, then the sum
$F_\infty$
, then the sum
![]() $\oplus_{w|v}$
is finite, and so
$\oplus_{w|v}$
is finite, and so
![]() $\ker\big(\oplus_{w|v}l_w\big)$
is cofinitely generated over
$\ker\big(\oplus_{w|v}l_w\big)$
is cofinitely generated over
![]() $\mathcal{O}_\eta$
for these v’s. Now suppose that v splits completely in
$\mathcal{O}_\eta$
for these v’s. Now suppose that v splits completely in
![]() $F_\infty$
. As noted in Remark 4·7,
$F_\infty$
. As noted in Remark 4·7,
![]() $\mathcal{A}(F_{\infty,w})[p_\eta] = A_{f_\eta}(F_{\infty,w})$
is finite for all v dividing p. For those primes not dividing p, the finiteness follows from assumption (a). Consequently,
$\mathcal{A}(F_{\infty,w})[p_\eta] = A_{f_\eta}(F_{\infty,w})$
is finite for all v dividing p. For those primes not dividing p, the finiteness follows from assumption (a). Consequently,
![]() $\mathcal{A}(F_{\infty,w})/P_\eta$
is finite by Lemma 2·1(iii) and is hence annihilated by some powers of p. This power of p annihilates
$\mathcal{A}(F_{\infty,w})/P_\eta$
is finite by Lemma 2·1(iii) and is hence annihilated by some powers of p. This power of p annihilates
![]() $\ker\big(\oplus_{w|v}l_w\big)$
. Therefore, we also have
$\ker\big(\oplus_{w|v}l_w\big)$
. Therefore, we also have
![]() $\ker\big(\oplus_{w|v}l_w\big)$
being cotorsion over
$\ker\big(\oplus_{w|v}l_w\big)$
being cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
for these primes. Hence we have shown that the kernel and cokernel of
$\mathcal{O}_\eta[[ \Gamma ]]$
for these primes. Hence we have shown that the kernel and cokernel of
![]() $r_\eta$
are cotorsion over
$r_\eta$
are cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
.
$\mathcal{O}_\eta[[ \Gamma ]]$
.
Combining this observation with hypothesis (b) of the theorem, we see that
![]() $R(\mathcal{A}/F_\infty)[p_\eta]$
is cotorsion over
$R(\mathcal{A}/F_\infty)[p_\eta]$
is cotorsion over
![]() $\mathcal{O}_\eta[[ \Gamma ]]$
. It then follows from Lemma 2·1(iii) that
$\mathcal{O}_\eta[[ \Gamma ]]$
. It then follows from Lemma 2·1(iii) that
![]() $R(\mathcal{A}/F_\infty)$
is cotorsion over
$R(\mathcal{A}/F_\infty)$
is cotorsion over
![]() $\mathcal{R}[[ \Gamma ]]$
. This proves the first assertion of the theorem.
$\mathcal{R}[[ \Gamma ]]$
. This proves the first assertion of the theorem.
In view of
![]() $\textbf{(H1)}$
, the ring
$\textbf{(H1)}$
, the ring
![]() $\mathcal{R}[[ \Gamma ]]$
is isomorphic to
$\mathcal{R}[[ \Gamma ]]$
is isomorphic to
![]() $\mathcal{O}[[ W, T ]]$
, where
$\mathcal{O}[[ W, T ]]$
, where
![]() $1+W$
(resp.,
$1+W$
(resp.,
![]() $1+T$
) corresponds to a topological generator of
$1+T$
) corresponds to a topological generator of
![]() $\Gamma$
(resp., a topological generator of
$\Gamma$
(resp., a topological generator of
![]() $\Gamma'$
). By the structure theorem (cf. [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7]), we then have a pseudo-isomorphism
$\Gamma'$
). By the structure theorem (cf. [Reference Neukirch, Schmidt and Wingberg40, proposition 5·1·7]), we then have a pseudo-isomorphism
of
![]() $\mathcal{R}[[ \Gamma ]]$
-modules, where I is some finite indexing set and each
$\mathcal{R}[[ \Gamma ]]$
-modules, where I is some finite indexing set and each
![]() $Q_i$
is a principal prime ideal of
$Q_i$
is a principal prime ideal of
![]() $\mathcal{R}[[ \Gamma ]]$
of height one. Since there are only finitely many
$\mathcal{R}[[ \Gamma ]]$
of height one. Since there are only finitely many
![]() $Q_i$
’s, for all but finitely many
$Q_i$
’s, for all but finitely many
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
, we have
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
, we have
![]() $Y(\mathcal{A}/F_\infty)/P_\lambda$
being torsion over
$Y(\mathcal{A}/F_\infty)/P_\lambda$
being torsion over
![]() $\mathcal{O}_{\lambda}[[ \Gamma ]]$
. From the above discussion, we see that
$\mathcal{O}_{\lambda}[[ \Gamma ]]$
. From the above discussion, we see that
has cokernel which is torsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
. It then follows that
$\mathcal{O}_\lambda[[ \Gamma ]]$
. It then follows that
![]() $Y\left(A_{f_{\lambda}}/F_\infty\right)$
is torsion over
$Y\left(A_{f_{\lambda}}/F_\infty\right)$
is torsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
for these
$\mathcal{O}_\lambda[[ \Gamma ]]$
for these
![]() $\lambda$
’s.
$\lambda$
’s.
The finiteness condition
![]() $H^0(F_v, A_{f_{\eta}})$
is known to hold in several cases (see [Reference Hatley, Kundu, Lei and Ray14, section 5·2]). In particular, if
$H^0(F_v, A_{f_{\eta}})$
is known to hold in several cases (see [Reference Hatley, Kundu, Lei and Ray14, section 5·2]). In particular, if
![]() $\eta$
comes from an elliptic curve, then this is always true, and so we have the following.
$\eta$
comes from an elliptic curve, then this is always true, and so we have the following.
Corollary 5·4.
Assume that (H1) and (H2) are valid. Suppose that there exists
![]() $\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
such that
$\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
such that
![]() $\mathcal{A}[P_\eta] \cong E[p^{\infty}]$
for some elliptic curve E with
$\mathcal{A}[P_\eta] \cong E[p^{\infty}]$
for some elliptic curve E with
![]() $R(E/F_\infty)$
cotorsion over
$R(E/F_\infty)$
cotorsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
.
$\mathbb{Z}_{p}[[ \Gamma ]]$
.
Then
![]() $R(\mathcal{A}/F_\infty)$
is cotorsion over
$R(\mathcal{A}/F_\infty)$
is cotorsion over
![]() $\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
$\mathcal{R}[[ \Gamma ]]$
. Furthermore, for all but finitely many
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
![]() $R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
$R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
.
$\mathcal{O}_\lambda[[ \Gamma ]]$
.
Proof. It remains to show that
![]() $H^0(F_v, E[p^{\infty}])$
is finite, but this is an immediate consequence of Mattuck’s theorem that
$H^0(F_v, E[p^{\infty}])$
is finite, but this is an immediate consequence of Mattuck’s theorem that
![]() $E(F_v)$
is finitely generated over
$E(F_v)$
is finitely generated over
![]() $\mathcal{O}_{F_v}$
(see [Reference Mattuck35]).
$\mathcal{O}_{F_v}$
(see [Reference Mattuck35]).
Comparing Theorems 4·3 and 5·3, one is naturally led to the following question.
Question
![]() $\mathcal{A}$
. Is
$\mathcal{A}$
. Is
![]() $Y(\mathcal{A}/F_\infty)$
pseudo-null over
$Y(\mathcal{A}/F_\infty)$
pseudo-null over
![]() $\mathcal{R}[[ \Gamma ]]$
?
$\mathcal{R}[[ \Gamma ]]$
?
To the best knowledge of the author, the structure of
![]() $R(\mathcal{A}/F_\infty)$
does not seem to be well-understood. Even in the context of a cyclotomic
$R(\mathcal{A}/F_\infty)$
does not seem to be well-understood. Even in the context of a cyclotomic
![]() $\mathbb{Z}_{p}$
-extension, it is still an open question whether
$\mathbb{Z}_{p}$
-extension, it is still an open question whether
![]() $R(\mathcal{A}/F_\infty)^\vee$
is finitely generated over
$R(\mathcal{A}/F_\infty)^\vee$
is finitely generated over
![]() $\mathcal{R}$
(see [Reference Jha and Sujatha17, conjecture 1]). There are some recent studies on this structure by Lei–Palvannan [Reference Lei and Palvannan25] in this direction. However, to the best knowledge of the author, the subject of the fine Selmer group of a Hida deformation over a general
$\mathcal{R}$
(see [Reference Jha and Sujatha17, conjecture 1]). There are some recent studies on this structure by Lei–Palvannan [Reference Lei and Palvannan25] in this direction. However, to the best knowledge of the author, the subject of the fine Selmer group of a Hida deformation over a general
![]() $\mathbb{Z}_{p}$
-extension does not seem to be covered in the literature. We can only hope to revisit this subject in a future study.
$\mathbb{Z}_{p}$
-extension does not seem to be covered in the literature. We can only hope to revisit this subject in a future study.
We end the section by specialising to the case of an imaginary quadratic field, where we explain how a conjecture of Mazur implies the various Conjecture Y’s. As a start, we recall the said conjecture of Mazur [Reference Mazur37].
Conjecture 5·5 (Growth Number Conjecture). Let E be an elliptic curve defined over
![]() $\mathbb{Q}$
and let K denote an imaginary quadratic field. The Mordell–Weil rank of E stays bounded along any
$\mathbb{Q}$
and let K denote an imaginary quadratic field. The Mordell–Weil rank of E stays bounded along any
![]() $\mathbb{Z}_{p}$
-extension of K, unless the extension is anticyclotomic and the root number is negative.
$\mathbb{Z}_{p}$
-extension of K, unless the extension is anticyclotomic and the root number is negative.
Theorem 5·6.
Assume that (H1) and (H2) are valid. Suppose that there exists
![]() $\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
such that
$\eta\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
such that
![]() $\mathcal{A}[P_\eta] \cong E[p^{\infty}]$
for some elliptic curve E. Let K be an imaginary quadratic field and
$\mathcal{A}[P_\eta] \cong E[p^{\infty}]$
for some elliptic curve E. Let K be an imaginary quadratic field and
![]() $K_\infty$
a
$K_\infty$
a
![]() $\mathbb{Z}_{p}$
-extension of K. Suppose that all of the following statements are valid.
$\mathbb{Z}_{p}$
-extension of K. Suppose that all of the following statements are valid.
-
(a) If
 $K_\infty$
is the anticyclotomic
$K_\infty$
is the anticyclotomic
 $\mathbb{Z}_{p}$
-extension, assume further that the root number is positive.
$\mathbb{Z}_{p}$
-extension, assume further that the root number is positive.
-
(b) The assertion of the growth number conjecture of Mazur is valid for the pair
 $(E, K_\infty)$
. In other words, the Mordell-Weil rank of E stays bounded along the
$(E, K_\infty)$
. In other words, the Mordell-Weil rank of E stays bounded along the
 $\mathbb{Z}_{p}$
-extension
$\mathbb{Z}_{p}$
-extension
 $K_\infty$
.
$K_\infty$
. -
(c) The fine Tate–Shafarevich group
 is finite for every n, where
is finite for every n, where
 $K_n$
is the intermediate subextension of
$K_n$
is the intermediate subextension of
 $K_\infty/K$
with
$K_\infty/K$
with
 $|K_n:K|=p^n$
.
$|K_n:K|=p^n$
.
Then
![]() $Y(\mathcal{A}/K_\infty)$
is torsion over
$Y(\mathcal{A}/K_\infty)$
is torsion over
![]() $\mathcal{R}[[ \Gamma ]]$
. Moreover, for all but finitely many
$\mathcal{R}[[ \Gamma ]]$
. Moreover, for all but finitely many
![]() $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
![]() $Y(A_{f_{\lambda}}/K_\infty)$
is torsion over
$Y(A_{f_{\lambda}}/K_\infty)$
is torsion over
![]() $\mathcal{O}_\lambda[[ \Gamma ]]$
.
$\mathcal{O}_\lambda[[ \Gamma ]]$
.
Proof. The growth number conjecture of Mazur implies that
![]() $E(K_\infty)$
is a finitely generated abelian group. Therefore, taking assumption (c) into account, we may apply Corollary 3·5 to conclude that
$E(K_\infty)$
is a finitely generated abelian group. Therefore, taking assumption (c) into account, we may apply Corollary 3·5 to conclude that
![]() $Y(E/F_\infty)$
is torsion over
$Y(E/F_\infty)$
is torsion over
![]() $\mathbb{Z}_{p}[[ \Gamma ]]$
. The theorem is now a consequence of a combination of this latter assertion and Corollary 5·4.
$\mathbb{Z}_{p}[[ \Gamma ]]$
. The theorem is now a consequence of a combination of this latter assertion and Corollary 5·4.
6. Examples
We give some examples to illustrate our results.
-
(i) Let E be the elliptic curve
 $y^2 + y = x^3 -x$
. Let
$y^2 + y = x^3 -x$
. Let
 $p=5$
. It is well-known that
$p=5$
. It is well-known that
 $\textrm{Sel}(E/\mathbb{Q}(\mu_{5^{\infty}})) =0$
(cf. [Reference Coates and Sujatha5, theorem 5·4]), where
$\textrm{Sel}(E/\mathbb{Q}(\mu_{5^{\infty}})) =0$
(cf. [Reference Coates and Sujatha5, theorem 5·4]), where
 $\textrm{Sel}(E/\mathbb{Q}(\mu_{5^{\infty}}))$
is the classical Selmer group. Let F be a finite Galois p-extension of
$\textrm{Sel}(E/\mathbb{Q}(\mu_{5^{\infty}}))$
is the classical Selmer group. Let F be a finite Galois p-extension of
 $\mathbb{Q}(\mu_5)$
. Then by [Reference Hachimori and Matsuno13, corollary 3·4],
$\mathbb{Q}(\mu_5)$
. Then by [Reference Hachimori and Matsuno13, corollary 3·4],
 $\textrm{Sel}(E/F^{\textrm{cyc}})$
is cotorsion over
$\textrm{Sel}(E/F^{\textrm{cyc}})$
is cotorsion over
 $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Since the fine Selmer group
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Since the fine Selmer group
 $R(E/F^{\textrm{cyc}})$
is contained in
$R(E/F^{\textrm{cyc}})$
is contained in
 $\textrm{Sel}(E/F^{\textrm{cyc}})$
, this in turn implies that
$\textrm{Sel}(E/F^{\textrm{cyc}})$
, this in turn implies that
 $R(E/F^{\textrm{cyc}})$
is cotorsion over
$R(E/F^{\textrm{cyc}})$
is cotorsion over
 $\mathbb{Z}_5[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Therefore, Theorem 3·9 applies. In other words, for any given
$\mathbb{Z}_5[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Therefore, Theorem 3·9 applies. In other words, for any given
 $\mathbb{Z}_5^2$
-extension
$\mathbb{Z}_5^2$
-extension
 $L_\infty$
of F containing
$L_\infty$
of F containing
 $F^{\textrm{cyc}}$
, for all but finitely many
$F^{\textrm{cyc}}$
, for all but finitely many
 $\mathbb{Z}_5$
-extension
$\mathbb{Z}_5$
-extension
 $F_\infty$
of F contained in
$F_\infty$
of F contained in
 $L_\infty$
, we have that
$L_\infty$
, we have that
 $R(E/F_\infty)$
is cotorsion over
$R(E/F_\infty)$
is cotorsion over
 $\mathbb{Z}_5[[ \textrm{Gal}(F_\infty/F) ]]$
.
$\mathbb{Z}_5[[ \textrm{Gal}(F_\infty/F) ]]$
.In view of Conjecture Y, we expect that
 $R(E/F_\infty)$
is cotorsion over
$R(E/F_\infty)$
is cotorsion over
 $\mathbb{Z}_5[[ \textrm{Gal}(F_\infty/F) ]]$
for all
$\mathbb{Z}_5[[ \textrm{Gal}(F_\infty/F) ]]$
for all
 $\mathbb{Z}_5$
-extensions of F. But this seems to be out of reach in general. (Note that Proposition 3·8 cannot apply here, since we do not have a good way of determining pseudo-nullity at our current state of knowledge.)
$\mathbb{Z}_5$
-extensions of F. But this seems to be out of reach in general. (Note that Proposition 3·8 cannot apply here, since we do not have a good way of determining pseudo-nullity at our current state of knowledge.)We however describe how one may obtain the absolute validity of Conjecture Y for the elliptic curve E in question over certain classes of 5-extensions of
 $\mathbb{Q}(\mu_5)$
. Let F be a finite Galois 5-extension of
$\mathbb{Q}(\mu_5)$
. Let F be a finite Galois 5-extension of
 $\mathbb{Q}(\mu_5)$
such that every ramified prime v of
$\mathbb{Q}(\mu_5)$
such that every ramified prime v of
 $F/\mathbb{Q}(\mu_5)$
outside 5 is neither a split multiplicative reduction prime of E nor a good reduction prime of E with
$F/\mathbb{Q}(\mu_5)$
outside 5 is neither a split multiplicative reduction prime of E nor a good reduction prime of E with
 $E(\mathbb{Q}(\mu_5)_v)[5]\neq 0$
. By Kida’s formula for elliptic curves (cf. [Reference Hachimori and Matsuno13, theorem 3·1]),
$E(\mathbb{Q}(\mu_5)_v)[5]\neq 0$
. By Kida’s formula for elliptic curves (cf. [Reference Hachimori and Matsuno13, theorem 3·1]),
 $\textrm{Sel}(E/F^{\textrm{cyc}})$
is finite which in turn implies that
$\textrm{Sel}(E/F^{\textrm{cyc}})$
is finite which in turn implies that
 $R(E/F^{\textrm{cyc}})$
is finite. It then follows from [Reference Lim28, theorem 3·3] that so is
$R(E/F^{\textrm{cyc}})$
is finite. It then follows from [Reference Lim28, theorem 3·3] that so is
 $R(E/F)$
. Applying Corollary 3·3, we see that Conjecture Y holds for every
$R(E/F)$
. Applying Corollary 3·3, we see that Conjecture Y holds for every
 $\mathbb{Z}_5$
-extension of F. Examples of such F’s are
$\mathbb{Z}_5$
-extension of F. Examples of such F’s are
 $\mathbb{Q}(\mu_{5^n}, 5^{-5^m})$
.
$\mathbb{Q}(\mu_{5^n}, 5^{-5^m})$
. -
(ii) The above discussion can also be applied to the elliptic curve
 $E: y^2 + xy = x^3 -x-1$
and
$E: y^2 + xy = x^3 -x-1$
and
 $p=7$
. Indeed, in this case, one has
$p=7$
. Indeed, in this case, one has
 $\textrm{Sel}(E/\mathbb{Q}(\mu_{7^{\infty}})) =0$
(cf. [Reference Coates and Sujatha5, theorem 5·31]). For more examples where the discussion in (i) also applies, we refer readers to the tables in [Reference Dokchitser and Dokchitser10] (basically look for those with
$\textrm{Sel}(E/\mathbb{Q}(\mu_{7^{\infty}})) =0$
(cf. [Reference Coates and Sujatha5, theorem 5·31]). For more examples where the discussion in (i) also applies, we refer readers to the tables in [Reference Dokchitser and Dokchitser10] (basically look for those with
 $\mathcal{L}_E(\sigma)$
being a unit).
$\mathcal{L}_E(\sigma)$
being a unit). -
(iii) Even if
 $\textrm{Sel}(E/\mathbb{Q}(\mu_{p^\infty}))\neq 0$
, there are many numerical examples (for instance, see [Reference Dokchitser and Dokchitser10, Reference Pollack46]), where the group
$\textrm{Sel}(E/\mathbb{Q}(\mu_{p^\infty}))\neq 0$
, there are many numerical examples (for instance, see [Reference Dokchitser and Dokchitser10, Reference Pollack46]), where the group
 $\textrm{Sel}(E/\mathbb{Q}(\mu_{p^\infty}))$
can be shown to be cofinitely generated over
$\textrm{Sel}(E/\mathbb{Q}(\mu_{p^\infty}))$
can be shown to be cofinitely generated over
 $\mathbb{Z}_{p}$
. By virtue of [Reference Hachimori and Matsuno13, corollary 3·4],
$\mathbb{Z}_{p}$
. By virtue of [Reference Hachimori and Matsuno13, corollary 3·4],
 $\textrm{Sel}(E/F^{\textrm{cyc}})$
is cofinitely generated over
$\textrm{Sel}(E/F^{\textrm{cyc}})$
is cofinitely generated over
 $\mathbb{Z}_{p}$
for every finite Galois p-extension F of
$\mathbb{Z}_{p}$
for every finite Galois p-extension F of
 $\mathbb{Q}(\mu_p)$
which in turn implies that
$\mathbb{Q}(\mu_p)$
which in turn implies that
 $R(E/F)$
is cofinitely generated over
$R(E/F)$
is cofinitely generated over
 $\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Hence we can at least apply Theorem 3·9 for these examples. We mention that the data in [Reference Pollack46] also consists of elliptic curves with supersingular reduction at p, where the plus-minus Selmer groups in the sense of Kobayashi [Reference Kobayashi22] have been verified to be cofinitely generated over
$\mathbb{Z}_{p}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Hence we can at least apply Theorem 3·9 for these examples. We mention that the data in [Reference Pollack46] also consists of elliptic curves with supersingular reduction at p, where the plus-minus Selmer groups in the sense of Kobayashi [Reference Kobayashi22] have been verified to be cofinitely generated over
 $\mathbb{Z}_{p}$
. As the fine Selmer group is contained in either of the plus-minus Selmer groups, the fine Selmer group is also cofinitely generated over
$\mathbb{Z}_{p}$
. As the fine Selmer group is contained in either of the plus-minus Selmer groups, the fine Selmer group is also cofinitely generated over
 $\mathbb{Z}_{p}$
. This cofinite generation of fine Selmer group is preserved under p-base change of fields (for instance, see the proof of [Reference Lim and Murty31, theorem 5·5]). Hence Theorem 3·9 applies for these examples.
$\mathbb{Z}_{p}$
. This cofinite generation of fine Selmer group is preserved under p-base change of fields (for instance, see the proof of [Reference Lim and Murty31, theorem 5·5]). Hence Theorem 3·9 applies for these examples. -
(iv) Let E be any elliptic curve in 49a and
 $F=\mathbb{Q}(E[7])$
. Take
$F=\mathbb{Q}(E[7])$
. Take
 $p=7$
. We shall show that Conjecture Y is valid for every
$p=7$
. We shall show that Conjecture Y is valid for every
 $\mathbb{Z}_7$
-extension of F. Indeed, this is plainly true if the
$\mathbb{Z}_7$
-extension of F. Indeed, this is plainly true if the
 $\mathbb{Z}_7$
-extension is the cyclotomic
$\mathbb{Z}_7$
-extension is the cyclotomic
 $\mathbb{Z}_7$
-extension by [Reference Rasmussen and Tamagawa48, corollary 8] and [Reference Coates and Sujatha4, corollary 3·6]. For a non-cyclotomic
$\mathbb{Z}_7$
-extension by [Reference Rasmussen and Tamagawa48, corollary 8] and [Reference Coates and Sujatha4, corollary 3·6]. For a non-cyclotomic
 $\mathbb{Z}_7$
-extension
$\mathbb{Z}_7$
-extension
 $F_\infty$
of F, the compositum of
$F_\infty$
of F, the compositum of
 $F_\infty$
and
$F_\infty$
and
 $F^{\textrm{cyc}}$
is a
$F^{\textrm{cyc}}$
is a
 $\mathbb{Z}_7^2$
-extension of F. By [Reference Lim26, section 4, example (a)],
$\mathbb{Z}_7^2$
-extension of F. By [Reference Lim26, section 4, example (a)],
 $Y(E/L_\infty)$
is pseudo-null. Therefore, the torsionness of
$Y(E/L_\infty)$
is pseudo-null. Therefore, the torsionness of
 $Y(E/F_\infty)$
follows from this and Proposition 3·8. For more of such examples, we refer readers to [Reference Lim26, section 4, example (a)] and [Reference Rasmussen and Tamagawa48, table 2].
$Y(E/F_\infty)$
follows from this and Proposition 3·8. For more of such examples, we refer readers to [Reference Lim26, section 4, example (a)] and [Reference Rasmussen and Tamagawa48, table 2]. -
(v) Let E be any elliptic curve in 32a and
 $F=\mathbb{Q}(\sqrt{-43})$
. Take
$F=\mathbb{Q}(\sqrt{-43})$
. Take
 $p=3$
. It has been verified by Lei-Palvannan that
$p=3$
. It has been verified by Lei-Palvannan that
 $R(E/L_\infty)$
is pseudo-null (see [Reference Lei and Palvannan24, section 8·4]), where
$R(E/L_\infty)$
is pseudo-null (see [Reference Lei and Palvannan24, section 8·4]), where
 $L_\infty$
is the
$L_\infty$
is the
 $\mathbb{Z}_3^2$
-extension of F. Therefore, we may apply Theorem 3·8 to obtain the validity of Conjecture Y for every
$\mathbb{Z}_3^2$
-extension of F. Therefore, we may apply Theorem 3·8 to obtain the validity of Conjecture Y for every
 $\mathbb{Z}_3$
-extension of F. [Reference Lei and Palvannan24, table 2] provides more examples, where Proposition 3·8 can be applied too.
$\mathbb{Z}_3$
-extension of F. [Reference Lei and Palvannan24, table 2] provides more examples, where Proposition 3·8 can be applied too. -
(vi) Let E be the elliptic curve 79a1 of Cremona’s tables given by
Let \[y^2 + xy +y =x^3 +x^2 -2x.\]
\[y^2 + xy +y =x^3 +x^2 -2x.\]
 $p=3$
and
$p=3$
and
 $F=\mathbb{Q}(\mu_3)$
. It has been computed by Wuthrich (see [Reference Dokchitser and Dokchitser10, p. 253]) that E(F) has
$F=\mathbb{Q}(\mu_3)$
. It has been computed by Wuthrich (see [Reference Dokchitser and Dokchitser10, p. 253]) that E(F) has
 $\mathbb{Z}$
-rank 1 and the Tate–Sharafevich group
$\mathbb{Z}$
-rank 1 and the Tate–Sharafevich group
 is finite. Under these observations, it follows from a similar argument to that in [Reference Coates and McConnell2, theorem 12] that one obtains
is finite. Under these observations, it follows from a similar argument to that in [Reference Coates and McConnell2, theorem 12] that one obtains
 $H^2(G_S(F),E[3^\infty]) = 0$
. By [Reference Hachimori12, lemma 3·2], this in turn implies that
$H^2(G_S(F),E[3^\infty]) = 0$
. By [Reference Hachimori12, lemma 3·2], this in turn implies that
 $R(E/F)$
is finite. Let
$R(E/F)$
is finite. Let
 $F_\infty$
be any
$F_\infty$
be any
 $\mathbb{Z}_3$
-extension of F. Then Theorem 3·3 applies to yield the torsionness of
$\mathbb{Z}_3$
-extension of F. Then Theorem 3·3 applies to yield the torsionness of
 $R(E/F_\infty)$
. As noted in [Reference Jha16, p. 362], the residual representation E[Reference Coates and Sujatha3] is irreducible. Let
$R(E/F_\infty)$
. As noted in [Reference Jha16, p. 362], the residual representation E[Reference Coates and Sujatha3] is irreducible. Let
 $\mathcal{F}$
be the Hida family associated to E. Applying Corollary 5·4, we see that for all but finitely many
$\mathcal{F}$
be the Hida family associated to E. Applying Corollary 5·4, we see that for all but finitely many
 $\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
$\lambda\in\mathfrak{X}_{\textrm{arith}}\left(h^{\textrm{ord}}_{\mathcal{F}}\right)$
,
 $R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
$R\left(A_{f_{\lambda}}/F_\infty\right)$
is cotorsion over
 $\mathcal{O}_\lambda[[ \textrm{Gal}(F_\infty/F) ]]$
.
$\mathcal{O}_\lambda[[ \textrm{Gal}(F_\infty/F) ]]$
.
7. Non-commutative speculation and further remarks
In this final section, we formulate an extension of Conjecture Y for a (possibly non-commutative) p-adic Lie extension. To simplify the discussion and for better clarity of the ideas behind, we shall restrict our attention to the context of the paper. However, it should be evident that much of the discussion here carries over to broader classes of Galois representations.
We shall let
![]() $\bar{A}$
denote either one of the following objects:
$\bar{A}$
denote either one of the following objects:
![]() $A[p^\infty], A_f, \mathcal{A}$
, and
$A[p^\infty], A_f, \mathcal{A}$
, and
![]() $\bar{R}$
the corresponding coefficients rings of these objects; namely, resp.,
$\bar{R}$
the corresponding coefficients rings of these objects; namely, resp.,
![]() $\mathbb{Z}_{p}, \mathcal{O}, \mathcal{R}$
. Note that in the context of
$\mathbb{Z}_{p}, \mathcal{O}, \mathcal{R}$
. Note that in the context of
![]() $\mathcal{A}$
, we still work under the hypotheses
$\mathcal{A}$
, we still work under the hypotheses
![]() $\textbf{(H1)}$
and
$\textbf{(H1)}$
and
![]() $\textbf{(H2)}$
. Let
$\textbf{(H2)}$
. Let
![]() $F_\infty$
be a p-adic Lie extension of F such that
$F_\infty$
be a p-adic Lie extension of F such that
![]() $G:=\textrm{Gal}(F_\infty/F)$
is pro-p with no p-torsion and that
$G:=\textrm{Gal}(F_\infty/F)$
is pro-p with no p-torsion and that
![]() $F_\infty/F$
is unramified outside a finite set of primes of F. The fine Selmer group of
$F_\infty/F$
is unramified outside a finite set of primes of F. The fine Selmer group of
![]() $\bar{A}$
over
$\bar{A}$
over
![]() $F_\infty$
, which is defined similarly as before, now has the structure of a
$F_\infty$
, which is defined similarly as before, now has the structure of a
![]() $\bar{R}[[ G ]]$
-module. We note that the ring
$\bar{R}[[ G ]]$
-module. We note that the ring
![]() $\bar{R}[[ G ]]$
is Auslander regular (cf. [Reference Venjakob52, theorem 3·26]; also see [Reference Lim27, theorem A·1]) and has no zero divisors (cf. [Reference Neumann41]). Therefore, there is a well-defined notion of torsion
$\bar{R}[[ G ]]$
is Auslander regular (cf. [Reference Venjakob52, theorem 3·26]; also see [Reference Lim27, theorem A·1]) and has no zero divisors (cf. [Reference Neumann41]). Therefore, there is a well-defined notion of torsion
![]() $\bar{R}[[ G ]]$
-modules and pseudo-null
$\bar{R}[[ G ]]$
-modules and pseudo-null
![]() $\bar{R}[[ G ]]$
-modules. For our purpose, a
$\bar{R}[[ G ]]$
-modules. For our purpose, a
![]() $\bar{R}[[ G ]]$
-module M is said to be torsion (resp., pseudo-null) if
$\bar{R}[[ G ]]$
-module M is said to be torsion (resp., pseudo-null) if
![]() $\textrm{Ext}_{\bar{R}[[ G ]]}^i(M,\bar{R}[[ G ]])=0$
for
$\textrm{Ext}_{\bar{R}[[ G ]]}^i(M,\bar{R}[[ G ]])=0$
for
![]() $i=0$
(resp.,
$i=0$
(resp.,
![]() $i=0,1$
). The following is then the natural generalization of Conjecture Y for a p-adic Lie extension.
$i=0,1$
). The following is then the natural generalization of Conjecture Y for a p-adic Lie extension.
Conjecture 7·1 (Generalised Conjecture Y). For every p-adic Lie extension
![]() $F_\infty$
of F,
$F_\infty$
of F,
![]() $Y(\bar{A}/F_\infty)$
is torsion over
$Y(\bar{A}/F_\infty)$
is torsion over
![]() $\bar{R}[[ G ]]$
.
$\bar{R}[[ G ]]$
.
For an abelian variety, the above conjecture was formulated in [Reference Kundu and Lim23] for a
![]() $\mathbb{Z}_{p}^d$
-extension of F.
$\mathbb{Z}_{p}^d$
-extension of F.
Remark 7·2. We now discuss a context closely related to the generalised Conjecture Y. Had we replaced
![]() $\bar{A}$
in the definition of the fine Selmer group by
$\bar{A}$
in the definition of the fine Selmer group by
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}(-i)$
(
$\mathbb{Q}_{p}/\mathbb{Z}_{p}(-i)$
(
![]() $i>0$
), where
$i>0$
), where
![]() $(-i)$
denotes the
$(-i)$
denotes the
![]() $(-i)$
th Tate twist, we will obtain the so-called étale wild kernel (for instance, see [Reference Nguyen Quang Do42, Reference Nguyen Quang Do43]). In this context, the author has established the torsionness of this group over every p-adic Lie extension (see [Reference Lim29, proposition 4·1·1] and [Reference Lim30, sections 3·2 and 3·3] for details). Therefore, this provides some optimism towards the generalised Conjecture Y.
$(-i)$
th Tate twist, we will obtain the so-called étale wild kernel (for instance, see [Reference Nguyen Quang Do42, Reference Nguyen Quang Do43]). In this context, the author has established the torsionness of this group over every p-adic Lie extension (see [Reference Lim29, proposition 4·1·1] and [Reference Lim30, sections 3·2 and 3·3] for details). Therefore, this provides some optimism towards the generalised Conjecture Y.
A similar argument to that in Theorem 3·9 yields the following.
Theorem 7·3.
Let
![]() $d\geq 2$
. Suppose that
$d\geq 2$
. Suppose that
![]() $L_{\infty}$
is a
$L_{\infty}$
is a
![]() $\mathbb{Z}_{p}^d$
-extension of F which contains
$\mathbb{Z}_{p}^d$
-extension of F which contains
![]() $F^{\textrm{cyc}}$
. Denote by
$F^{\textrm{cyc}}$
. Denote by
![]() $\Phi_d(L_\infty/F)$
the set of all
$\Phi_d(L_\infty/F)$
the set of all
![]() $\mathbb{Z}_{p}^{d-1}$
-extensions of F contained in
$\mathbb{Z}_{p}^{d-1}$
-extensions of F contained in
![]() $L_\infty$
. Assume that
$L_\infty$
. Assume that
![]() $R(\bar{A}/F^{\textrm{cyc}})$
is cotorsion over
$R(\bar{A}/F^{\textrm{cyc}})$
is cotorsion over
![]() $\bar{R}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
$\bar{R}[[ \textrm{Gal}(F^{\textrm{cyc}}/F) ]]$
. Then for all but finitely many
![]() $\mathcal{L}\in\Phi_d(L_\infty/F)$
,
$\mathcal{L}\in\Phi_d(L_\infty/F)$
,
![]() $R(\bar{A}/\mathcal{L})$
is cotorsion over
$R(\bar{A}/\mathcal{L})$
is cotorsion over
![]() $\bar{R}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
.
$\bar{R}[[ \textrm{Gal}(\mathcal{L}/F) ]]$
.
We finally end by providing a conceptual explanation on why the postulation of Conjecture Y over a general p-adic Lie extension is plausible. To give this explanation, we now recall the generalised Conjecture B of Coates–Sujatha [Reference Coates and Sujatha4] and Jha [Reference Jha16].
Conjecture 7·4. If
![]() $F_\infty$
is a p-adic Lie extension of F of dimension
$F_\infty$
is a p-adic Lie extension of F of dimension
![]() $>1$
containing
$>1$
containing
![]() $F^{\textrm{cyc}}$
, then
$F^{\textrm{cyc}}$
, then
![]() $Y(\bar{A}/F_\infty)$
is pseudo-null over
$Y(\bar{A}/F_\infty)$
is pseudo-null over
![]() $\bar{R}[[ G ]]$
.
$\bar{R}[[ G ]]$
.
Proposition 7·5.
Suppose that Conjecture 7·4 is valid for every p-adic Lie extension of F of dimension
![]() $>1$
containing
$>1$
containing
![]() $F^{\textrm{cyc}}$
. Then the generalised Conjecture Y is valid for every p-adic Lie extension of F of dimension
$F^{\textrm{cyc}}$
. Then the generalised Conjecture Y is valid for every p-adic Lie extension of F of dimension
![]() $>1$
.
$>1$
.
Proof. We first make the following remark. Let G be a compact p-adic Lie group and M a
![]() $\bar{R}[[ G ]]$
-module. For every open subgroup
$\bar{R}[[ G ]]$
-module. For every open subgroup
![]() $G_0$
of G, we then have
$G_0$
of G, we then have
(cf. [Reference Neukirch, Schmidt and Wingberg40, proposition 5·4·17]). Therefore, the question of M being torsion (resp., pseudo-null) over
![]() $\bar{R}[[ G ]]$
is equivalent to M being torsion (resp., pseudo-null) over
$\bar{R}[[ G ]]$
is equivalent to M being torsion (resp., pseudo-null) over
![]() $\bar{R}[[ G_0 ]]$
.
$\bar{R}[[ G_0 ]]$
.
Now let
![]() $F_\infty$
be a p-adic Lie extension of F of dimension
$F_\infty$
be a p-adic Lie extension of F of dimension
![]() $>1$
. If
$>1$
. If
![]() $F_\infty$
contains
$F_\infty$
contains
![]() $F^{\textrm{cyc}}$
, then by the assumption of the proposition,
$F^{\textrm{cyc}}$
, then by the assumption of the proposition,
![]() $Y(\bar{A}/F_\infty)$
is pseudo-null over
$Y(\bar{A}/F_\infty)$
is pseudo-null over
![]() $\bar{R}[[ G ]]$
, and hence is also torsion over
$\bar{R}[[ G ]]$
, and hence is also torsion over
![]() $\bar{R}[[ G ]]$
. Suppose that
$\bar{R}[[ G ]]$
. Suppose that
![]() $F^{\textrm{cyc}}$
is not contained in
$F^{\textrm{cyc}}$
is not contained in
![]() $F_\infty$
. Then
$F_\infty$
. Then
![]() $F^{\textrm{cyc}}\cap F_\infty$
is a finite extension of F. In view of the the remark in the first paragraph, we see that neither the hypothesis nor the conclusion is affected if we replace F by
$F^{\textrm{cyc}}\cap F_\infty$
is a finite extension of F. In view of the the remark in the first paragraph, we see that neither the hypothesis nor the conclusion is affected if we replace F by
![]() $F^{\textrm{cyc}}\cap F_\infty$
. Hence, upon relabelling, we might as well assume that
$F^{\textrm{cyc}}\cap F_\infty$
. Hence, upon relabelling, we might as well assume that
![]() $F=F^{\textrm{cyc}}\cap F_\infty$
. Therefore, writing
$F=F^{\textrm{cyc}}\cap F_\infty$
. Therefore, writing
![]() $L_\infty =F^{\textrm{cyc}} \cdot F_\infty$
, we have
$L_\infty =F^{\textrm{cyc}} \cdot F_\infty$
, we have
![]() $\mathcal{G}:=\textrm{Gal}(L_\infty/F)\cong Z\times G$
, where
$\mathcal{G}:=\textrm{Gal}(L_\infty/F)\cong Z\times G$
, where
![]() $Z\cong\textrm{Gal}(F^{\textrm{cyc}}/F)$
. Let z be a topological generator of Z. Then for every
$Z\cong\textrm{Gal}(F^{\textrm{cyc}}/F)$
. Let z be a topological generator of Z. Then for every
![]() $\bar{R}[[ \mathcal{G} ]]$
-module M, we have
$\bar{R}[[ \mathcal{G} ]]$
-module M, we have
![]() $M_Z = M/(z-1)$
which can be viewed as a
$M_Z = M/(z-1)$
which can be viewed as a
![]() $\bar{R}[[ G ]]$
-module. As Z is central in
$\bar{R}[[ G ]]$
-module. As Z is central in
![]() $\mathcal{G}$
,
$\mathcal{G}$
,
![]() $M_Z$
may also be viewed as a
$M_Z$
may also be viewed as a
![]() $\bar{R}[[ \mathcal{G} ]]$
-module. In particular,
$\bar{R}[[ \mathcal{G} ]]$
-module. In particular,
is a
![]() $\bar{R}[[ \mathcal{G} ]]$
-free resolution of the
$\bar{R}[[ \mathcal{G} ]]$
-free resolution of the
![]() $\bar{R}[[ \mathcal{G} ]]$
-module
$\bar{R}[[ \mathcal{G} ]]$
-module
![]() $\bar{R}[[ G ]]$
. Via a spectral sequence argument similar to that in Lemma 2·1, we obtain
$\bar{R}[[ G ]]$
. Via a spectral sequence argument similar to that in Lemma 2·1, we obtain
In particular, one has
Since
![]() $Y(\bar{A}/L_\infty)$
is pseudo-null over
$Y(\bar{A}/L_\infty)$
is pseudo-null over
![]() $\bar{R}[[ \mathcal{G} ]]$
by hypothesis, the latter is zero. From which, we see that
$\bar{R}[[ \mathcal{G} ]]$
by hypothesis, the latter is zero. From which, we see that
![]() $Y(\bar{A}/L_\infty)_{Z}$
is torsion over
$Y(\bar{A}/L_\infty)_{Z}$
is torsion over
![]() $\bar{R}[[ G ]]$
. On the other hand, a descent argument as in Theorem 3·9 yields a map
$\bar{R}[[ G ]]$
. On the other hand, a descent argument as in Theorem 3·9 yields a map
whose cokernel is a quotient of
![]() $H^1(Z, \bar{A}(L_\infty))^\vee$
, where the latter is plainly finitely generated over
$H^1(Z, \bar{A}(L_\infty))^\vee$
, where the latter is plainly finitely generated over
![]() $\bar{R}$
. It then follows that
$\bar{R}$
. It then follows that
![]() $Y(\bar{A}/F_\infty)$
is torsion over
$Y(\bar{A}/F_\infty)$
is torsion over
![]() $\bar{R}[[ G ]]$
as required.
$\bar{R}[[ G ]]$
as required.
Acknowledgments
The author likes to thank Somnath Jha, Debanjana Kundu, Antonio Lei and Bharathwaj Palvannan for their interest and comments on initial drafts of the paper. He would like to thank the anonymous referee for several helpful comments and suggestions. The author’s work is supported by the National Natural Science Foundation of China under Grant No. 11771164 and the Fundamental Research Funds for the Central Universities of CCNU under Grant No. CCNU20TD002.