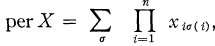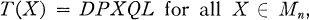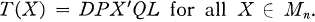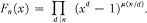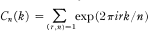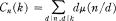Research Article
Contributions to the Cell Growth Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-20
-
- Article
-
- You have access
- Export citation
A Census of Planar Triangulations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-38
-
- Article
-
- You have access
- Export citation
Transcendental Elements in Continuous Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-44
-
- Article
-
- You have access
- Export citation
The Clifford Algebra and the Group of Similitudes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-59
-
- Article
-
- You have access
- Export citation
Study of Certain Similitudes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-68
-
- Article
-
- You have access
- Export citation
Univalent Solutions of W″ + pW = 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-78
-
- Article
-
- You have access
- Export citation
Symmetric Exterior Differentiation and Flat Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-86
-
- Article
-
- You have access
- Export citation
A Generalization of Finsler Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-112
-
- Article
-
- You have access
- Export citation
Embedding Circle-Like Continua in the Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-128
-
- Article
-
- You have access
- Export citation
Some Results on Quadrics in Finite Projective Geometry Based on Galois Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-138
-
- Article
-
- You have access
- Export citation
Homotopy Theory in Abelian Categories
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-169
-
- Article
-
- You have access
- Export citation
Weakly Compact Sets in Orlicz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-176
-
- Article
-
- You have access
- Export citation
The Permanent Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 177-189
-
- Article
-
- You have access
- Export citation
Permanent Preservers on the Space of Doubly Stochastic Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-194
-
- Article
-
- You have access
- Export citation
On Finite Groups of the Form ABA
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 195-236
-
- Article
-
- You have access
- Export citation
Weak Containment and Induced Representations of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 237-268
-
- Article
-
- You have access
- Export citation
Uniform Boundedness for Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 269-276
-
- Article
-
- You have access
- Export citation
Generators for Simple Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-283
-
- Article
-
- You have access
- Export citation
Some Formulas Involving Ramanujan Sums
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-286
-
- Article
-
- You have access
- Export citation
Some Lie Admissible Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 287-292
-
- Article
-
- You have access
- Export citation

 as a generalization to the infinite limiting case of the total matric algebras over a division ring. Von Neumann sketched a theory of arithmetic for such continuous rings
as a generalization to the infinite limiting case of the total matric algebras over a division ring. Von Neumann sketched a theory of arithmetic for such continuous rings 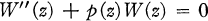
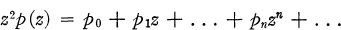
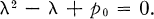
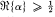 . Corresponding to the root
. Corresponding to the root 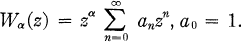
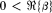 there exists a unique second solution of (1.1) of the form
there exists a unique second solution of (1.1) of the form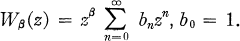
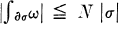 for every
for every