Published online by Cambridge University Press: 20 November 2018
The purpose of this note is to establish an identity involving the cyclotomic polynomial and a function of the Ramanujan sums. Some consequences are then derived from this identity.
For the reader desiring a background in cyclotomy, (2) is mentioned. Also, (4) is intimately connected with the following discussion and should be consulted.
The cyclotomic polynomial Fn(x) is defined as the monic polynomial whose roots are the primitive nth roots of unity. It is well known that
2.1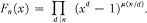
For the proof of Corollary 3.2 it is mentioned that Fn(0) = 1 if n > 1 and that Fn(x) > 0 if |x| < 1 and 1 < n.
The Ramanujan sums are defined by
2.2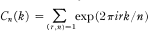
where the sum is taken over all positive integers r less than or equal to n and relatively prime to n. It is also well known that
2.3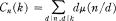
where the sum is taken over all positive divisors d common to n and k.