Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carlson, B. C.
and
Shaffer, Dorothy B.
1984.
Starlike and Prestarlike Hypergeometric Functions.
SIAM Journal on Mathematical Analysis,
Vol. 15,
Issue. 4,
p.
737.
Shah, S.M.
1988.
Univalence of a function f and its successive derivatives when f satisfies a differential equation.
Journal of Mathematical Analysis and Applications,
Vol. 133,
Issue. 1,
p.
79.
Baricz, Árpád
Kupán, Pál
and
Szász, Róbert
2014.
The radius of starlikeness of normalized Bessel functions of the first kind.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 6,
p.
2019.
Baricz, Árpád
and
Szász, Róbert
2014.
The radius of convexity of normalized Bessel functions of the first kind.
Analysis and Applications,
Vol. 12,
Issue. 05,
p.
485.
Baricz, Árpád
Orhan, Halit
and
Szász, Róbert
2016.
The Radius of $$\alpha $$ α -Convexity of Normalized Bessel Functions of the First Kind.
Computational Methods and Function Theory,
Vol. 16,
Issue. 1,
p.
93.
Baricz, Árpád
Deniz, Erhan
and
Yağmur, Nihat
2016.
Close‐to‐convexity of normalized Dini functions.
Mathematische Nachrichten,
Vol. 289,
Issue. 14-15,
p.
1721.
Baricz, Árpád
and
Nemes, Gergő
2021.
Asymptotic expansions for the radii of starlikeness of normalised Bessel functions.
Journal of Mathematical Analysis and Applications,
Vol. 494,
Issue. 2,
p.
124624.
Nazir, Maryam
Bukhari, Syed Zakar Hussain
Ahmad, Imtiaz
Ashfaq, Muhammad
Raza, Malik Ali
and
Yalçın, Sibel
2021.
Starlikeness of Normalized Bessel Functions with Symmetric Points.
Journal of Function Spaces,
Vol. 2021,
Issue. ,
p.
1.
Baricz, Árpád
Kumar, Pranav
and
Singh, Sanjeev
2023.
On starlikeness of regular Coulomb wave functions.
Proceedings of the American Mathematical Society,
Gangania, Kamaljeet
and
Kumar, S. Sivaprasad
2024.
Certain radii problems for 𝓢∗(ψ) and special functions.
Mathematica Slovaca,
Vol. 74,
Issue. 1,
p.
69.
Baricz, Árpád
Kumar, Pranav
and
Singh, Sanjeev
2024.
Asymptotic Expansions for the Radii of Starlikeness of Normalized q-Bessel Functions.
Results in Mathematics,
Vol. 79,
Issue. 7,


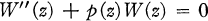
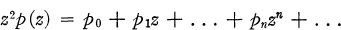
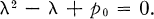
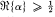 . Corresponding to the root
. Corresponding to the root 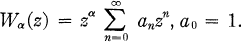
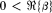 there exists a unique second solution of (1.1) of the form
there exists a unique second solution of (1.1) of the form