Let ω be a continuous differential r-form defined in a bounded domain R of Euclidean n-space, En, where n ≧ 1 and 0 ≦ r ≦ n — 1. ω is called a flat form in R, (3, p. 263), if there exists a constant N such that 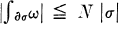for every (r + 1)-simplex σ contained in R, where |σ| designates the (r + 1)-volume of σ. For n = 1 and ω a zero form, flatness is the same thing as the usual Lip 1 condition. As is well known, a necessary and sufficient condition that a continuous real-valued function of one variable f(x) satisfy a Lip 1 condition over an interval (a, b) is that its upper and lower symmetric derivatives be bounded in (a, b) (4, pp. 22, 327). We intend to prove the analogue of this result for r-forms.