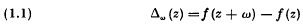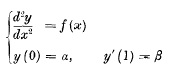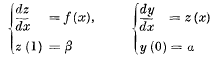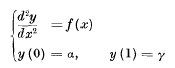Research Article
James Gregory: A Study in the Early History of Interpolation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-172
-
- Article
-
- You have access
- Export citation
On Small Deformation of Sub-Spaces of a Flat Space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 77-86
-
- Article
-
- You have access
- Export citation
Interpolation by means of Given Differences (Central-Difference Notation)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
Sets of Semi-Commutative Matrices: Part II1
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 231-240
-
- Article
-
- You have access
- Export citation
Sets of Points Self-Conjugate with regard to a Quadric in n Dimensions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 6-9
-
- Article
-
- You have access
- Export citation
On Absolute Summability for any Positive Order
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 173-178
-
- Article
-
- You have access
- Export citation
On the asymptotic periods of integral functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 241-258
-
- Article
-
- You have access
- Export citation
On Functions of Integrals
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 87-98
-
- Article
-
- You have access
- Export citation
Factorial Moments and Frequencies of Charlier's Type B
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-106
-
- Article
-
- You have access
- Export citation
The Composition of Linear Differential Systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 10-15
-
- Article
-
- You have access
- Export citation
The Jacobian Curve of a Net of Quadrics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 259-268
-
- Article
-
- You have access
- Export citation
Sets of Semi-Commutative Matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 179-188
-
- Article
-
- You have access
- Export citation
Metrical Coordinates in Non-Euclidean Geometry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 16-25
-
- Article
-
- You have access
- Export citation
On Errors in Determinants
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-117
-
- Article
-
- You have access
- Export citation
A Matrix Representation of Ascending and Descending Continued Fractions1
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 189-200
-
- Article
-
- You have access
- Export citation
On Straneo's Unified Theory of Gravitation and Electricity
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 269-275
-
- Article
-
- You have access
- Export citation
A Note on Resultants of Equations in a Cyclic Number System
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 26-29
-
- Article
-
- You have access
- Export citation
Bessel-integral functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 276-285
-
- Article
-
- You have access
- Export citation
An Approximation connected with e-x
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 201-206
-
- Article
-
- You have access
- Export citation
Certain Expansions in the Algebra of Quantum Mechanics1
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 118-127
-
- Article
-
- You have access
- Export citation

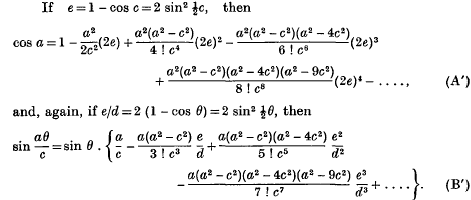

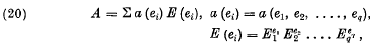
 and its
and its  , by
, by  we can regard
we can regard  as the sum of the series
as the sum of the series