Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T11:20:00.387Z Has data issue: false hasContentIssue false
  • English
  • Français

James Gregory: A Study in the Early History of Interpolation

Published online by Cambridge University Press:  20 January 2009

H. W. Turnbull
H. W. Turnbull
Affiliation:
University of St Andrews.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a highly interesting critical account of the mathematical work of James Gregory (1638–1675), written for the Proceedings of the Edinburgh Mathematical Society, (1) 41 (1923), 2–25, by the late Professor G. A. Gibson, there occurs at p. 8 something of a mathematical puzzle. On that page a pair of formulae are quoted, which certainly are striking examples of the analytical power of Gregory, and which run as follows:—

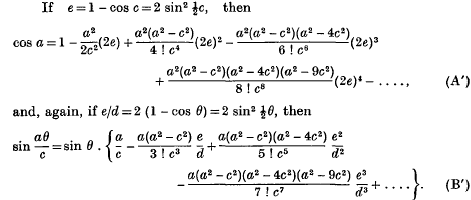
Gibson adds that “there is another formula (Rigaud, p. 207), but it is of a very complicated character and I do not reproduce it.” It will be convenient to refer to the above pair as formulae A′ and B′, and to the more complicated but analogous series as formula C, and to the original series, from which the above were transcribed, as formulse A and B. I am indebted to Mr A. Inglis for drawing my attention to the problem.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , Issue 3 , February 1933 , pp. 151 - 172
Copyright
Copyright © Edinburgh Mathematical Society 1933

References

BIBLIOGRAPHY

Gibson, Proc. Edinburgh Math. Soc., I, 41 (1922), 2–25; and II, 1 (1927), 1–18.CrossRefGoogle Scholar
Rigaud, Correspondence of Scientific Men, of the Seventeenth Century, 2, 185–211. Commercium Epistolicum D. Johannis Collins et Aliorum de Analysi Promota (London, 1712).Google Scholar
Briggs, Arithmetica Logarithmica (London, 1624), 24–32.Google Scholar
Briggs, Trigonometria Britannica (1633), 12–52.Google Scholar
Vieta, Opera Mathematica: edited by Schooten (1646), 287–324.Google Scholar
Hutton, Tracts on Mathematical Subjects, 1, Tract 12, 228–244; Tracts 19, 20, 21.Google Scholar
Maurice, Journal of the Institute of Actuaries, 14 (1869), 1, who quotes Legendre's Connaissance des Termes (1817).Google Scholar
Whittaker, and Robinson, , The Calculus of Observations (Glasgow, 1926), 1–52.Google Scholar