Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T18:30:33.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets of Semi-Commutative Matrices

Published online by Cambridge University Press:  20 January 2009

J. Williamson
J. Williamson
Affiliation:
(Johns Hopkins University).
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a paper entitled “Sets of anticommuting matrices” Eddington proved that if El, E2, …., Eqform a set of q four-rowed square matrices satisfying the relations,

,

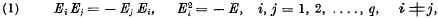where E is the unit matrix, then the maximum value of q is five. Later Newman showed that this result is a particular case of the general theorem that ifE1, E2, …., Eqform a set of q t-rowed square matrices satisfying (1), where t = 2Pτ and τ is odd, then the maximum value of q is 2p + 1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , Issue 3 , February 1933 , pp. 179 - 188
Copyright
Copyright © Edinburgh Mathematical Society 1933

References

page 179 note 1 Journal London Math. Soc., 7 (1932), 58–68.Google Scholar

page 179 note 2 ibrid.. 7 (1932), 94–99.

page 181 note 1 See Dickson, L. E.Algebras and their Arithmetics, p. 72.Google Scholar

page 183 note 1 If ω is a primitive nth root of unity, is a primitive 2nth root of unity. A primitive nth root of unity satisfies an equation of degree φ (n), irreducible in the field of rational numbers, where φ (n) is the Euler φ-function. If n = 2sk, where k is odd, Thus the degrees of the irreducible equations satisfied by ω and are different. Hence the fields R(ω) and R() cannot coincide. This is no longer true if n is odd, since, if n = 2 f + 1, = ωf+1.

page 188 note 1 As both Bddington and Newman consider matrices whose squares are —E, the number of imaginary matrices in a set of such matrices is the same as the number of real matrices in an E-set, satisfying (2) with n = 2.Google Scholar