Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T07:09:56.006Z Has data issue: false hasContentIssue false
  • English
  • Français

The Composition of Linear Differential Systems

Published online by Cambridge University Press:  20 January 2009

J. M. Whittaker
J. M. Whittaker
Affiliation:
Pembroke College, Cambridge.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A common method of solving a linear differential equation consists in expressing the differential operator as a product of factors. The possibility of doing so has been studied extensively by Vessiot, following the work of Picard and Drach, on the lines of the Galois theory of algebraic equations. The analogous process of resolving a, linear differential system, consisting of an equation together with boundary conditions, into two or more systems of lower order does not seem to have been investigated. Such a resolution is not always possible, even in cases where the differential equation can be factorised. Thus the system

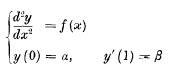
is equivalent to the systems

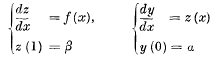
but the system

cannot be so resolved.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , Issue 1 , March 1932 , pp. 10 - 15
Copyright
Copyright © Edinburgh Mathematical Society 1932

References

page 10 note 1 See the account in Picard's Traité d'Analyse, 3 (1928), chap. 17.Google Scholar

page 12 note 1 CfInce, , Ordinary Differential Equations (1927), 254.Google Scholar

page 12 note 2 CfVolterra, , Theory of Functionals (1930), 99.Google Scholar

page 14 note 1 Bôcher, , Annals of Mathematics, 13 (1911), 71–88. Not K(ζ, x) as sometimes stated.CrossRefGoogle Scholar

page 14 note 2 Math. Ann., 63 (1907), 433–476. p. 461.CrossRefGoogle Scholar

page 14 note 3 CfSchmidt, , loc. cit.,Google Scholar or Courant-Hilbert, , Methoden der Mathematischen Physik, 1 (1924), 137.Google Scholar

page 15 note 1 Ince, , op. cit., 256. (αy) is assumed to be incompatible.Google Scholar