Research Article
On the foundations of inverse monoids and inverse algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-21
-
- Article
-
- You have access
- Export citation
The Cartan determinant and generalizations of quasihereditary rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 23-32
-
- Article
-
- You have access
- Export citation
Radial functions on compact support
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 33-46
-
- Article
-
- You have access
- Export citation
Hypoelliptic differential operators with generalized constant coefficients
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 47-60
-
- Article
-
- You have access
- Export citation
Construction of Schauder decomposition on banach spaces of periodic functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 61-91
-
- Article
-
- You have access
- Export citation
On some “stability” properties of the full C*-algebra associated to the free group F∞
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 93-116
-
- Article
-
- You have access
- Export citation
Nonlinear periodic parabolic problems with nonmonotone discontinuities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 117-132
-
- Article
-
- You have access
- Export citation
The spectra of Toeplitz operators with unimodular symbols
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 133-139
-
- Article
-
- You have access
- Export citation
Geometrically finite kleinian groups and parabolic elements
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 141-159
-
- Article
-
- You have access
- Export citation
Closed ideals in the Banach algebra ℓ1(ω) when ω is ∈-star shaped
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 161-176
-
- Article
-
- You have access
- Export citation
Generalized blocked triangular matrix rings associated with finite abelian centralizer near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 177-195
-
- Article
-
- You have access
- Export citation
A measure of non-immersability of the Grassmann manifolds in some euclidean spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 197-205
-
- Article
-
- You have access
- Export citation
Book Reviews
J. W. S. Cassels and E. V. Flynn Prolegomena to a middlebrow arithmetic of curves of genus 2 (London Mathematical Society Lecture Note Series Vol. 230, Cambridge University Press, Cambridge, 1996), xiv + 219pp., 0 521 48370 0 (paperback) £22.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 207
-
- Article
-
- You have access
- Export citation
L. J. Mason and N. M. J. Woodhouse Integrability, self-duality and twistor theory (London Mathematical Society Monographs (New Series) No. 15, Clarendon Press, Oxford, 1996), x + 364pp., 0 19 853498 1, (hardback) £45.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 208
-
- Article
-
- You have access
- Export citation
A. Kanamori The higher infinite: large cardinals in set theory from their beginnings (Perspectives in Mathematical Logic, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong, 1994), xxiv + 536 pp., 3 540 57071 3, £77.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 208-209
-
- Article
-
- You have access
- Export citation
S. Shelah Cardinal arithmetic (Oxford Logic Guides Vol. 29, Clarendon Press, Oxford, 1994), xxxi + 481 pp., 0 19 853785 9, (hardback) £65.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 209-210
-
- Article
-
- You have access
- Export citation
A. Iserles A first course in the numerical analysis of differential equations (Cambridge University Press, Cambridge, 1996), xvi + 378pp., 0 521 55655 4 (paperback) £19.95 (US$27.95), 0 521 55376 8 (hardback) £55 (US$74.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 211
-
- Article
-
- You have access
- Export citation
M. Audin Spinning Tops (Cambridge Studies in Advanced Mathematics Vol. 51, Cambridge University Press, Cambridge, 1996), viii + 139pp., 0 521 56129 9, (hardback) £25 (US$34.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 211-213
-
- Article
-
- You have access
- Export citation
A. M. Stuart and A. R. Humphries Dynamical systems and numerical analysis (Cambridge Monographs on Applied and Computational Mathematics No. 2, Cambridge University Press, 1996), xxii + 685 pp., 0 521 49672 1, (hardback) £40 (US$59.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 213-216
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 41 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

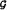 of Colombeau generalized functions is used as a frame for the study of hypoellipticity of a family of differential operators whose coefficients depend on a small parameter ε.
of Colombeau generalized functions is used as a frame for the study of hypoellipticity of a family of differential operators whose coefficients depend on a small parameter ε.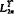 on one hand and by interpolatory projections in the Banach space
on one hand and by interpolatory projections in the Banach space 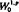 (
(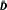 are given. In particular if φ is a unimodular function in
are given. In particular if φ is a unimodular function in