Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:43:47.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypoelliptic differential operators with generalized constant coefficients

Published online by Cambridge University Press:  20 January 2009

M. Nedeljkov  and
S. Pilipović
M. Nedeljkov
Affiliation:
University of Novi Sad, Faculty of Science, Institute for Mathematics, TRG D. Obradovića 4, Novi Sad, Yugoslavia
S. Pilipović
Affiliation:
University of Novi Sad, Faculty of Science, Institute for Mathematics, TRG D. Obradovića 4, Novi Sad, Yugoslavia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space 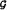of Colombeau generalized functions is used as a frame for the study of hypoellipticity of a family of differential operators whose coefficients depend on a small parameter ε.

There are given necessary and sufficient conditions for the hypoellipticity of a family of differential operators with constant coefficients which depend on ε and behave like powers of ε as ε→0. The solutions of such family of equations should also satisfy the power order estimate with respect to ε.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 41 , Issue 1 , February 1998 , pp. 47 - 60
Copyright
Copyright © Edinburgh Mathematical Society 1998

References

REFERENCES

1.Colombeau, J. F., Elementary Introduction in New Generalized Functions (North Holland, Amsterdam, 1985).Google Scholar
2.Friedman, A., Generalized unctions and Partial Differential Equations (Prentice-Hall, Inc, Englewood Cliffs, New York, 1963).Google Scholar
3.Gorin, E. A., Asymptotic properties of polynomials and algebraic functions of several variables, Russian Math. Surveys (1961), 93–119.CrossRefGoogle Scholar
4.Li Bang-He, , Non-standard analysis and multiplication of distributions, Sci. Sinica 21 (1978), 561–585.Google Scholar
5.Oberguggenberger, M., Multiplication of Distributions and Applications to Partial Differential Equations (Pitman Res. Not. Math. 259, Longman Sci. Techn., Essex, 1992).Google Scholar
6.Oberguggenberger, M., Products of Distributions: Nonstandard Methods, Z. Anal. Anwendungen 7 (12) (1988), 347–365.CrossRefGoogle Scholar
7.Pilipović, S. and Scarpalézos, D., Differential operators with generalized constant coefficients, Portugal. Math. 53 (3) (1996), 305–324.Google Scholar