Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T05:45:12.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Construction of Schauder decomposition on banach spaces of periodic functions

Published online by Cambridge University Press:  20 January 2009

Say Song Goh ,
S. L. Lee ,
Zuowei Shen  and
W. S. Tang
Say Song Goh
Affiliation:
Department of Mathematics, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, Republic of Singapore
S. L. Lee
Affiliation:
Department of Mathematics, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, Republic of Singapore
Zuowei Shen
Affiliation:
Department of Mathematics, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, Republic of Singapore
W. S. Tang
Affiliation:
Department of Mathematics, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, Republic of Singapore
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with Schauder decompositions of Banach spaces X2π of 2π-periodic functions by projection operators Pk onto the subspaces Vk, k = 0,1,…, which form a multiresolution of X2π,. The results unify the study of wavelet decompositions by orthogonal projections in the Hilbert space 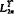on one hand and by interpolatory projections in the Banach space C2π on the other. The approach, using “orthogonal splines”, is constructive and leads to the construction of a Schauder decomposition of X2π and a biorthogonal system for X2π, and its dual X2π. Decomposition and reconstruction algorithms are derived from the construction.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 41 , Issue 1 , February 1998 , pp. 61 - 91
Copyright
Copyright © Edinburgh Mathematical Society 1998

References

REFERENCES

1.Carnicer, J. M., Dahmen, W. and Peña, J. M., Local decomposition of refinable spaces and wavelets, Appl. Comput. Harmonic Anal. 3 (1996), 127–153.CrossRefGoogle Scholar
2.Chui, C. K. and Li, C., Dyadic affine decompositions and functional wavelet transformations, SIAM J. Math. Anal. 27 (1996), 865–890.CrossRefGoogle Scholar
3.Chui, C. K. and Mhaskar, N. H., On trigonometric wavelets, Constr. Approx. 9 (1993), 167–190.CrossRefGoogle Scholar
4.Dahmen, W., Some remarks on multiscale transformations, stability and biorthogonality, in Curves and Surfaces II (Laurent, P. J., Le Méhauté, A. and Schumaker, L. L., eds., Academic Press, San Diego, 1994), 157–188.Google Scholar
5.Dahmen, W., Stability of multiscale transformations, preprint.Google Scholar
6.Daubechies, I., Orthonormal bases of compactly supported wavelets, Comm. Pure Appl. Math. 41 (1988), 909–996.CrossRefGoogle Scholar
7.Donoho, D. L., Interpolating wavelet transform, preprint.Google Scholar
8.Katznelson, Y., An Introduction to Harmonic Analysis (Dover, New York, 1976).Google Scholar
9.Koh, Y. W., Lee, S. L. and Tan, H. H., Periodic orthogonal splines and wavelets, Appl. Comput. Harmonic Anal. 2 (1995), 201–218.CrossRefGoogle Scholar
10.Mallat, S., Multiresolution approximations and wavelet orthonormal bases of L 2(R), Trans. Amer. Math. Soc. 315 (1989), 69–87.Google Scholar
11.Marti, J. T., Introduction to the Theory of Bases (Springer-Verlag, New York, 1969).CrossRefGoogle Scholar
12.Micchelli, C. A., Using refinement equation for the construction of pre-wavelets, Numerical Algorithm 1 (1991), 75–116.CrossRefGoogle Scholar
13.Narcowich, F. J. and Ward, J. D., Wavelets associated with periodic basis functions, Appl. Comput. Harmonic Anal. 3 (1996), 40–56.CrossRefGoogle Scholar
14.Plonka, G. and Tasche, M., A unified approach to periodic wavelets, in Wavelets: Theory, Algorithms, and Applications (Chui, C. K., Montefusco, L. and Puccio, L., eds., Academic Press, New York, 1994), 137–151.Google Scholar
15.Reiter, H., Classical Harmonic Analysis and Locally Compact Groups (Oxford University Press, London, 1968).Google Scholar