Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:43:38.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear periodic parabolic problems with nonmonotone discontinuities

Published online by Cambridge University Press:  20 January 2009

Dimitrios A. Kandilakis  and
Nikolaos S. Papageorgiou
Dimitrios A. Kandilakis
Affiliation:
Department of Mathematics, University of the Aegean, 83200 Karlovassi Samos, Greece
Nikolaos S. Papageorgiou
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus 15780 Athens, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider a nonlinear periodic parabolic boundary value problem with a discontinuous nonmonotone nonlinearity. Using a lifting result for operators of type (S+), a general surjectivity theorem for operators of monotone type and an auxiliary problem defined by truncation and penalization we prove the existence of a solution in the order interval formed by an upper and lower solution. Moreover we show that the set of all such solutions is compact in Lp(T, 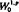(Z)).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 41 , Issue 1 , February 1998 , pp. 117 - 132
Copyright
Copyright © Edinburgh Mathematical Society 1998

References

REFERENCES

1.Ash, R., Real Analysis and Probability (Academic Press, New York, 1972).Google Scholar
2.Carl, S. and Heikkila, S., On a parabolic boundary value problem with discontinuous nonlinearity, Nonlinear Anal. 15(1990), 1091–1095.CrossRefGoogle Scholar
3.Chang, K.-C., Variational methods for nondifferentiable functionals and their applications to partial differential equations, J. Math. Anal. Appl. 80 (1981), 102–129.CrossRefGoogle Scholar
4.Deuel, J. and Hess, P., Nonlinear parabolic boundary value problems with upper and lower solutions, Israel. Math. 29 (1978), 92–104.CrossRefGoogle Scholar
5.Diestel, J. and Uhl, J., Vector Measures (Math. Surveys, 15, AMS, Providence, Rhode Island, 1977).CrossRefGoogle Scholar
6.Feireisl, E., A note on uniqueness for parabolic problems with discontinuous nonlinearities, Nonlinear Anal. 16(1991), 1053–1056.CrossRefGoogle Scholar
7.Feireisl, E. and Norbury, J., Some existence, uniqueness and nonuniqueness theorems for solutions of parabolic equations with discontinuous nonlinearities, Proc. Roy. Soc. Edinburgh 119A (1991), 1–17.CrossRefGoogle Scholar
8.Filippov, V., Differential equations with discontinuous right hand side, Mat. Sb. 51 (1960), 99–128 (English Trans.: Transl. Amer. Math. Soc. 42 (1964), 199–232).Google Scholar
9.Gilbarg, D. and Trudinger, N., Elliptic Partial Differential Equations of Second Order (Springer Verlag, New York, 1977).CrossRefGoogle Scholar
10.Kufner, A. and Fučik, O. J.-S., Function Spaces (Noordhoff, Dordrecht, The Netherlands, 1977).Google Scholar
11.Lions, J.-L., Quelques Methodes de Resolution des Problemes aux Limites Non-Linearies (Dunod, Paris, 1969).Google Scholar
12.Papageorgiou, N. S., Convergence theorems for Banach space valued integrable multifunctions, Internat. J. Math. Math. Sci. 10 (1987), 433–442.CrossRefGoogle Scholar
13.Rauch, J., Discontinuous semilinear differential equations and multiple valued maps, Proc. Amer. Math. Soc. 84 (1977), 277–282.CrossRefGoogle Scholar
14.Stuart, C., Maximal and minimal solutions of elliptic differential equations with discontinuous nonlinearities, Math. Z. 163 (1978), 239–249.CrossRefGoogle Scholar
15.Ton, B.-A., Nonlinear evolution equations in Banach spaces, J.Differential Equations 9 (1971), 608–618.CrossRefGoogle Scholar
16.Zeidler, E., Nonlinear Functional Analysis and its Applications II (Springer Verlag, New York, 1990).Google Scholar
17.Zhikov, V., Kozlov, S. and Oleinik, O., G-convergence of parabolic operators, Russian Math. Surveys 36 (1981), 9–60.CrossRefGoogle Scholar