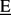Research Article
Some entries in Ramanujan's notebooks
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 255-266
-
- Article
- Export citation
On the intersection of free subgroups in free products of groups
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 511-534
-
- Article
- Export citation
Frobenius n-homomorphisms, transfers and branched coverings
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 1-12
-
- Article
- Export citation
Averages in vector spaces over finite fields
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 13-27
-
- Article
- Export citation
Characteristic elements, pairings and functional equations over the false Tate curve extension
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 535-574
-
- Article
- Export citation
Asymptotic density in quasi-logarithmic additive number systems
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 267-287
-
- Article
- Export citation
On the lines passing through two conjugates of a Salem number
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 29-37
-
- Article
- Export citation
The Nilpotent filtration and the action of automorphisms on the cohomology of finite p-groups
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 575-602
-
- Article
- Export citation
Additive structures in sumsets
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 289-316
-
- Article
- Export citation
Iterated realizability as a comma construction
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 39-51
-
- Article
- Export citation
Jordan homomorphisms revisited
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 317-328
-
- Article
- Export citation
The Brauer–Manin obstruction on del Pezzo surfaces of degree 2 branched along a plane section of a Kummer surface
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 603-622
-
- Article
- Export citation
An algebra-level version of a link-polynomial identity of Lickorish
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 623-638
-
- Article
- Export citation
Periodic cohomology and subgroups with bounded Bredon cohomological dimension
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 329-336
-
- Article
- Export citation
Elementary remarks on units in monoidal categories
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 53-76
-
- Article
- Export citation
Third Mac Lane cohomology
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 337-367
-
- Article
- Export citation
Uniqueness of bridge surfaces for 2-bridge knots
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 639-650
-
- Article
- Export citation
On the action of the Hua subgroups in special Moufang sets
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 77-84
-
- Article
- Export citation
On ϕ-amenability of Banach algebras
-
- Published online by Cambridge University Press:
- 01 January 2008, pp. 85-96
-
- Article
- Export citation
Torelli groups, extended Johnson homomorphisms, and new cycles on the moduli space of curves
-
- Published online by Cambridge University Press:
- 01 May 2008, pp. 651-671
-
- Article
- Export citation

 the free product of
the free product of 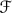 denote the set of all finitely generated subgroups
denote the set of all finitely generated subgroups 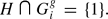 By the Kurosh Subgroup Theorem, every element of
By the Kurosh Subgroup Theorem, every element of 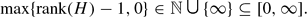 To avoid the vacuous case, we make the additional assumption that
To avoid the vacuous case, we make the additional assumption that 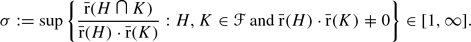
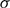 . In the special case where
. In the special case where 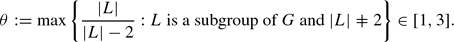
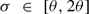 , and, moreover,
, and, moreover, 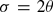 whenever
whenever 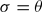 whenever
whenever 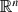 when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.
when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.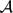 all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function
all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function 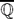 of degree
of degree 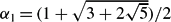 shows that this equation has such a solution.
shows that this equation has such a solution.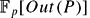 –module. In particular, we study the conjecture, first considered by Martino and Priddy, that, if
–module. In particular, we study the conjecture, first considered by Martino and Priddy, that, if 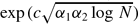 where α
where α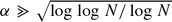 then
then 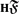 with periodic cohomology after some steps has finite cohomological dimension. In this note we look at similar questions for groups with torsion by considering Bredon cohomology. In particular we show that every elementary amenable group acting freely and properly on some
with periodic cohomology after some steps has finite cohomological dimension. In this note we look at similar questions for groups with torsion by considering Bredon cohomology. In particular we show that every elementary amenable group acting freely and properly on some 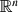 ×
×