Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T08:46:23.888Z Has data issue: false hasContentIssue false
  • English
  • Français

On the intersection of free subgroups in free products of groups

Published online by Cambridge University Press:  01 May 2008

WARREN DICKS  and
S. V. IVANOV
WARREN DICKS
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, E-08193 Bellaterra (Barcelona), Spain. e-mail: [email protected]
S. V. IVANOV
Affiliation:
Department of Mathematics, University of Illinois at Urbana–Champaign, 1409 West Green Street, Urbana IL 61801, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (Gi | i ∈ I) be a family of groups, let F be a free group, and let the free product of F and all the Gi.

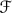Let denote the set of all finitely generated subgroups H of G which have the property that, for each g ∈ G and each i ∈ I, 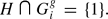By the Kurosh Subgroup Theorem, every element of 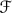is a free group. For each free group H, the reduced rank of H, denoted r(H), is defined as 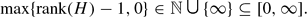To avoid the vacuous case, we make the additional assumption that 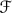contains a non-cyclic group, and we define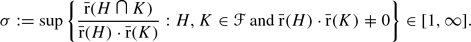We are interested in precise bounds for 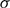. In the special case where I is empty, Hanna Neumann proved that 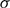∈ [1,2], and conjectured that 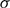= 1; fifty years later, this interval has not been reduced.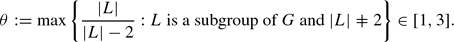

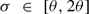With the understanding that ∞/(∞ − 2) is 1, we define

Generalizing Hanna Neumann's theorem we prove that , and, moreover, 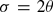whenever G has 2-torsion. Since 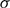is finite, 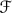is closed under finite intersections. Generalizing Hanna Neumann's conjecture, we conjecture that 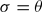whenever G does not have 2-torsion.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 3 , May 2008 , pp. 511 - 534
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bass, H.. Covering theory for graphs of groups. J. Pure Appl. Algebra 89 (1993), 3–47.CrossRefGoogle Scholar
[2]Baumslag, B.. Intersections of finitely generated subgroups in free products. J. London Math. Soc. 41 (1966), 673–679.CrossRefGoogle Scholar
[3]Burns, R. G.. On the intersection of finitely generated subgroups of a free group. Math. Z. 119 (1971), 121–130.CrossRefGoogle Scholar
[4]Burns, R. G., C, T.. Chau normalfont and S. M. Kam. On the rank of intersection of subgroups of a free product of groups. J. Pure Appl. Algebra 124 (1998), 31–45.CrossRefGoogle Scholar
[5]Cauchy, A. L.. Recherches sur les nombres. J. École Polytechnique 9 (1813), 99–116.Google Scholar
[6]Cohen, D. E.. Subgroups of HNN groups. J. Austral. Math. Soc. 17 (1974), 394–405.CrossRefGoogle Scholar
[7]Davenport, H.. On the addition of residue classes. J. London Math. Soc. 10 (1935), 30–32.CrossRefGoogle Scholar
[8]Dicks, W.. Equivalence of the strengthened Hanna Neumann conjecture and the amalgamated graph conjecture. Invent. Math. 117 (1994), 373–389. Errata at http://mat.uab.cat/~dicks/InvErr.htmlCrossRefGoogle Scholar
[9]Dicks, W. and Dunwoody, M. J.. Groups acting on graphs. Cambridge Studies in Advance Math 17. (Cambridge University Press, 1989). Errata at http://mat.uab.cat/~dicks/DDerr.htmlGoogle Scholar
[10]Dicks, W. and Formanek, E.. The rank three case of the Hanna Neumann Conjecture. J. Group Theory 4 (2001), 113–151.CrossRefGoogle Scholar
[11]Gersten, S. S.. Intersections of finitely generated subgroups of free groups and resolutions of graphs. Invent. Math. 71 (1983), 567–591.CrossRefGoogle Scholar
[12]Howson, A. G.. On the intersection of finitely generated free groups. J. London Math. Soc. 29 (1954), 428–434.CrossRefGoogle Scholar
[13]Imrich, W.. On finitely generated subgroups of free groups. Arch. Math. 28 (1977), 21–24.CrossRefGoogle Scholar
[14]Ivanov, S. V.. On the intersection of finitely generated subgroups in free products of groups. Int. J. Algebra Comp. 9 (1999), 521–528.CrossRefGoogle Scholar
[15]Ivanov, S. V.. Intersecting free subgroups in free products of groups. Int. J. Algebra Comp. 11 (2001), 281–290.CrossRefGoogle Scholar
[16]H, J.. Kemperman, B.. On complexes in a semigroup. Indag. Math. 18 (1956), 247–254.Google Scholar
[17]ück, W. L.. L 2-invariants: theory and applications to geometry and K-theory. Ergeb. Math. Grenzgeb. (3) 44 (2002).Google Scholar
[18]Mann, H. B.. A proof of the fundamental theorem on the density of sums of sets of positive integers. Ann. Math. (2) 43 (1942), 523–527.CrossRefGoogle Scholar
[19]Neumann, H.. On intersections of finitely generated subgroups of free groups. Addendum Publ. Math. Debrecen 4 (1956), 186–189.CrossRefGoogle Scholar
[20]Neumann, H.. On intersections of finitely generated subgroups of free groups. Addendum. Publ. Math. Debrecen 5 (1957), 128.CrossRefGoogle Scholar
[21]Neumann, W. D.. On intersections of finitely generated subgroups of free groups. pp. 161–170 in Groups - Canberra 1989 (ed. Kovfics, L. G.), Lect. Notes Math. 1456. (Springer, Berlin, 1990).Google Scholar
[22]Serre, J. P.. Trees. (Springer-Verlag, 1980).CrossRefGoogle Scholar
[23]Shimura, G.. Introduction to the Arithmetic Theory of Automorphic Forms (Princeton University Press, 1971).Google Scholar
[24]Soma, T.. Intersection of finitely generated surface groups. J. Pure Appl. Algebra 66 (1990), 81–95.CrossRefGoogle Scholar
[25]R, J.. Stallings. Topology of finite graphs. Invent. Math. 71 (1983), 551–565.Google Scholar
[26]Sykiotis, M.. On subgroups of finite complexity in groups acting on trees. J. Pure Appl. Algebra 200 (2005), 1–23.CrossRefGoogle Scholar
[27]Tardos, G.. On the intersection of subgroups of a free group. Invent. Math. 108 (1992), 29–36.CrossRefGoogle Scholar
[28]Tardos, G.. Towards the Hanna Neumann conjecture using Dicks' method. Invent. Math. 123 (1996), 95–104.CrossRefGoogle Scholar