Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-30T19:41:11.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Averages in vector spaces over finite fields

Published online by Cambridge University Press:  01 January 2008

ANTHONY CARBERY ,
BRENDAN STONES  and
JAMES WRIGHT
ANTHONY CARBERY
Affiliation:
School of Mathematics and Maxwell Institute of Mathematical Sciences, University of Edinburgh, JCMB, King's Buildings, Mayfield Road, Edinburgh, EH9 3JZ, Scotland. e-mail: [email protected]
BRENDAN STONES
Affiliation:
The John Henry Newman School, Hitchin Road, Stevenage, Hertfordshire, G1 4AE. e-mail: [email protected]
JAMES WRIGHT
Affiliation:
School of Mathematics and Maxwell Institute of Mathematical Sciences, University of Edinburgh, JCMB, King's Buildings, Mayfield Road, Edinburgh, EH9 3JZ, Scotland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

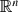We study the analogues of the problems of averages and maximal averages over a surface in when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 1 , January 2008 , pp. 13 - 27
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourgain, J., Katz, N. and Tao, T.. A sum-product estimate in finite fields, and applications, Geom. Funct. Anal. 14, no. 1 (2004), 27–57.Google Scholar
[2]Carlitz, L. and Uchiyama, S., Bounds for exponential sums, Duke Math. Jour. 24, (1957) 37–41.Google Scholar
[3]Christ, M.. Estimates for the k-plane transform. Indiana U. Math. J. 33, no. 6 (1984), 891–910.CrossRefGoogle Scholar
[4]Christ, M.. Convolution, curvature, and combinatorics: a case study. Internat. Math. Res. Notices 19 (1998), 1033–1048.CrossRefGoogle Scholar
[5]Deligne, P.. La conjecture de Weil, I. Inst. Hautes Etudes Sci. Publ. Math. 43 (1974), 273–307.Google Scholar
[6]Mockenhoupt, G. and Tao, T.. Restriction and Kakeya phenomena for finite fields. Duke Math. J. 121 2 (2004), 35–74.Google Scholar
[7]Stones, B.. Three aspects of harmonic analysis over finite fields, Ph.D. thesis. University of Edinburgh (2005).Google Scholar
[8]Schlag, W.. On continuum incidence problems related to harmonic analysis. J. Funct. Anal. 201 2 (2003), 480–521.CrossRefGoogle Scholar
[9]Seeger, A.. Degenerate Fourier integral operators in the plane. Duke Math. J. 71 (1993), 685–745.Google Scholar
[10]Stein, E. M.. Harmonic Analysis (Princeton University Press 1993).Google Scholar
[11]Tao, T. and Wright, J.. Lp-improving estimates for averages along curves. J. Amer. Math. Soc 16 (2003), 605–638.Google Scholar
[12]Weil, A.. On some exponential sums. Proc. Nat. Acad. Sci. U.S.A 34 (1948), 204–207.Google Scholar
[13]Wolff, T.. Recent work connected with the Kakeya problem. Prospects in Mathematics (Princeton, NJ, 1996), Amer. Math. Soc. (1999), 129–162.Google Scholar