Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T18:22:59.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive structures in sumsets

Published online by Cambridge University Press:  01 March 2008

TOM SANDERS
TOM SANDERS*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge, CB3 0WA. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that A and A′ are subsets of ℤ/Nℤ. We write A+A′ for the set {a+a′:a ∈ A and a′ ∈ A′} and call it the sumset of A and A′. In this paper we address the following question. Suppose that A1,. . .,Am are subsets of ℤ/Nℤ. Does A1+· · ·+Am contain a long arithmetic progression?

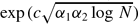The situation for m=2 is rather different from that for m ≥ 3. In the former case we provide a new proof of a result due to Green. He proved that A1+A2 contains an arithmetic progression of length roughly where α1 and α2 are the respective densities of A1 and A2. In the latter case we improve the existing estimates. For example we show that if A ⊂ ℤ/Nℤ has density 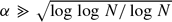then A+A+A contains an arithmetic progression of length Ncα. This compares with the previous best of Ncα2+ϵ.

Two main ingredients have gone into the paper. The first is the observation that one can apply the iterative method to these problems using some machinery of Bourgain. The second is that we can localize a result due to Chang regarding the large spectrum of L2-functions. This localization seems to be of interest in its own right and has already found one application elsewhere.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 289 - 316
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourgain, J.On triples in arithmetic progression. Geom. Funct. Anal. 9 (1999), no. 5, 968–984.CrossRefGoogle Scholar
[2]Chang, M.-C.. A polynomial bound in Freiman's theorem. Duke Math. J. 113 (2002), no. 3, 399–419.CrossRefGoogle Scholar
[3]Croot, E.k-term arithmetic progressions in very sparse sumsets. Preprint.Google Scholar
[4]Green, B.J.Arithmetic progressions in sumsets. Geom. Funct. Anal. 12 (2002), no. 3, 584–597.CrossRefGoogle Scholar
[5]Green, B.J. Restriction and Kakeya phenomena. http://www.maths.bris.ac.uk/~mabjg.Google Scholar
[6]Green, B.J. and Tao, T. An inverse theorem for the Gowers U 3(G)-norm. Preprint.Google Scholar
[7]Rudin, W.Fourier analysis on groups. Interscience Tracts in Pure and Applied Mathematics, No. 12 (Interscience Publishers (a division of John Wiley and Sons), 1962) ix+285 pp.Google Scholar
[8]Ruzsa, I.Z.Generalized arithmetical progressions and sumsets. Acta Math. Hungar. 65 (1994), no. 4, 379–388.CrossRefGoogle Scholar
[9]Tao, T. The Roth–Bourgain theorem. http://www.math.ucla.edu/~tao.Google Scholar
[10]Tao, T. Lecture notes in additive combinatorics. http://www.math.ucla.edu/~tao.Google Scholar
[11]Tao, T. and Vu, V.Additive combinatorics. Cambridge Studies in Advanced Mathematics, 105 (Cambridge University Press, 2006), xviii+512 pp.CrossRefGoogle Scholar