In 1858 Chebyshev, and some years later his students Korkin and Zolotarev, determined the polynomial which deviates least from zero among all polynomials of degree n with leading coefficient one with respect to the maximum- and the L1-norm, respectively; these are now called the Chebyshev polynomial of first and second kind.
The next natural step which is to find, at least asymptotically, the minimal polynomial with respect to a given weight function has not been settled until today. Indeed, Bernstein gave asymptotics for the minimum deviation of weighted minimal polynomials, Fekete and Walsh found nth root asymptotics and, recently, Lubinsky and Saff provided asymptotics outside [−1, 1]. But the main point of interest: the asymptotic representation of the weighted minimal polynomials on the interval of approximation [−1, 1] remained open. Here we settle this problem with respect to the maximum norm for weight functions whose second derivative is Lipα, α ∈ (0, 1), and with respect to the L1-norm under somewhat stronger differentiability conditions.
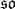 (7)
(7)

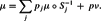
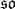 (7)
(7)
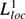 and be of polynomial growth. We use an apparently new technical lemma that implies that certain bounded approximate identities for
and be of polynomial growth. We use an apparently new technical lemma that implies that certain bounded approximate identities for 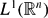 are also topological approximate identities for elements of the space
are also topological approximate identities for elements of the space 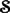 of Schwartz functions.
of Schwartz functions.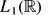 the Haar wavelet basis is not equivalent to any permutation with any signs of the Strω wavelet basis. We also construct a Haar-type system in
the Haar wavelet basis is not equivalent to any permutation with any signs of the Strω wavelet basis. We also construct a Haar-type system in