For countable admissible α, one can add a new infinitary propositional connective to 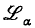so that the extended language obeys the Barwise compactness theorem, and the set of valid sentences is complete α-r.e.

Aside from obeying the compactness theorem and a completeness theorem, ordinary finitary predicate calculus is also truth-functionally complete.

In (1), Barwise shows that for countable admissible A, 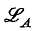provides a fragment of 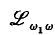which obeys a compactness theorem and a completeness theorem. However, we of course lose truth-functional completeness, with respect to infinitary propositional connectives that operate on infinite sequences of propositional variables. This raises the question of studying extensions of the language 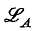obtained by adding infinitary propositional connectives, in connexion with the Barwise compactness and completeness theorems, and other metatheorems, proved for 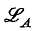Some aspects of this project are proposed in (3). It is the purpose of this paper to answer a few of the more basic questions which arise in this connexion.

We have not attempted to study the preservation of interpolation or implicit definability. This could be quite interesting if done systematically.

1. Introduction. The Nullstellensatz in commutative algebraic geometry may be described as a means of studying certain commutative rings (viz. affine algebras) by their homomorphisms into algebraically closed fields, and a number of attempts have been made to extend the result to the non-commutative case. In particular, Amitsur and Procesi have studied the case of general rings, with homomorphisms into matrix rings over commutative fields ((1), (2)) and Procesi has obtained more precise results for homomorphisms of PI-rings (11). Since a finite-dimensional division algebra can always be embedded in a matrix ring over a field, this includes the case of skew fields that are finite-dimensional over their centre, but it tells us nothing about general skew fields.

A group G is said to be complete if the centre of G is trivial and every automorphism of G is inner; this means that G is naturally isomorphic to Aut G, the group of automorphisms of G. In response to a question of Rose (10) we shall describe the construction of an example demonstrating the following result. (Rose has pointed out that the problem was mentioned earlier by Miller (8).)

1. Cremona's projection of 15 lines on a nodal cubic surface onto a plane π is a striking example of the resolution of a highly complicated figure into its constituent simplicities, for it explains, almost at a glance, so many properties of Pascal's mystic hexagram. These may appropriately be called ((12); (10), p. 162) the Veronese properties and have been described on several occasions ((12); (6); (10); (1), pp. 219–236; (2), pp. 349–355).

1. Introduction. The main purpose of this paper is to present a generalization of Hirzebruch's signature theorem for the case of manifolds with boundary. Our result is in the framework of Riemannian geometry and can be viewed as analogous to the Gauss–Bonnet theorem for manifolds with boundary, although there is a very significant difference between the two cases which is, in a sense, the central topic of the paper. To explain this difference let us begin by recalling that the classical Gauss–Bonnet theorem for a surface X with boundary Y asserts that the Euler characteristic E(X) is given by a formula:

where K is the Gauss curvature of X and σ is the geodesic curvature of Y in X. In particular if, near the boundary, X is isometric to the product Y x R+, the boundary integral in (1.1) vanishes and the formula is the same as for closed surfaces. Similar remarks hold in higher dimensions. Now if X is a closed oriented Riemannian manifold of dimension 4, there is another formula relating cohomological invariants with curvature in addition to the Gauss–Bonnet formula. This expresses the signature of the quadratic form on H2(X, R) by an integral formula

where p1 is the differential 4-form representing the first Pontrjagin class and is given in terms of the curvature matrix R by p1 = (2π)−2Tr R2. It is natural to ask if (1.2) continues to hold for manifolds with boundary, provided the metric is a product near the boundary. Simple examples show that this is false, so that in general

My aim in this paper is to give an abstract characterization of the C∞ spaces described in (6) or (9), and to develop some of the remarkable special properties of these spaces. Although the subject is in some ways highly specialized, inextensible and sequentially inextensible spaces seem common enough (they include all spaces of the forms Rx and L0) to be worth studying, and I have already employed them in the proof of more general results (1).

In the first section I set out those properties that can be described in simple Riesz space terms; much of this work has already been published in slightly different forms. In the second part I go on to questions that arise when we impose a topology on an inextensible Riesz space. Finally, in the third section, I discuss some problems, arising from the work before, which are related to the famous measurable cardinal problem.

1. Introduction. The spaces L1 and L2 of unbounded operators associated with a regular gauge space (von Neumann algebra equipped with a faithful normal semi-finite trace) are defined by Segal(5) definitions 3.3, 3.7. The spaces Lp (1 < p < ∞, p ± 2) are defined by Dixmier(2) as the abstract completions of their bounded parts. Dixmier makes use of the Riesz convexity theorem to prove the Hölder inequality, and the uniform convexity, and hence reflexivity, of LLp (2 < p < ∞).

1. Introduction. Using throughout the definitions and notations contained in (4), we state the following recent results by one of the present authors ((4), Theorem I and Theorem 2) which include as a special case the corresponding |C| – result due to Bosanquet (1), Bosanquet and Hyslop (2) and Hyslop(5).

1. Jurkat and Peyerimhoff(3) (or see (4), pages 50–56) have given a definition of a function, f(A), of an infinite matrix A = (ank). In particular, they considered Aα, where a is any real constant. This is defined wherever A is normal; that is to say, when ank = 0 for k > n, and when, for all n, ann ±0. They also defined the ‘Cesàro iteration’ Aα. This is obtained by defining a matrix B = (bnn) by

(so that every diagonal element of B is 1), forming Bα, and then dividing each row by the row sum; that is to say, if Bα = (b(α)nk), we take

where

The definition requires, of course, that ≠ 0.

Let

be regular in U = {|z| < 1}. Suppose that the values of f(z) all lie in a domain D in the w-plane. If certain geometrical restrictions are made on D we can deduce growth conditions on the maximum modulus

the means

and the coefficients αn. Good bounds for M(r, f) have been obtained under various conditions on D.

1. During the past decade a variety of integral transformations have been extended to various classes of distributions. However, one important integral transformation, which has defied such generalization, is the Kontorovich–Lebedev transformation. The objective of this note is to alter that situation.

Further consideration is given to properties of the Stokes phenomenon associated with a class of nth order differential equations with transition points of order m (a rational fraction) at the origin. The systematic vanishing of the Stokes multipliers leads to the discovery of sets of equations that are transformable from certain specific values of m to particular lower values of m. A series of theorems in the theory of congruences is first proved, from which the main transformation theorem is then deduced. The theory is ifiustrated by various numerical examples.

During the last thirty years an immense amount of research has been done on differential equations of the form

where ε > 0 is small. It is usually assumed that the perturbing term on the right-hand side is a ‘good’ function of its arguments and that its dependence on t is purely trigonometric; this means that there is an expansion of the form

where the ωn are constants, and that one may impose any conditions on the rate of convergence of the series which turn out to be convenient. Without loss of generality we can assume

and for convenience we shall sometimes write ω0 = 0. Often f is assumed to be periodic in t, in which case it is implicit that the period is independent of x and ẋ (We can also allow f to depend on ε, provided it does so in a sensible manner.)

A geometrical representation of the transition matrices of a non-homogeneous chain with N states, in terms of certain convex subsets of , is used to describe aspects of the chain. For example, an important theorem of Cohn on the structure of the tail σ-field is a simple corollary. The embedding problem is shown to be entirely geometrical in character. The representation extends to Markov processes on quite general state spaces, and the tail is then represented by the projective limit of these convex sets.

We introduce the idea of dissociatedness for multiply-subscripted random variables: this is a weaker property than independence in general, coinciding with it in the singly-subscripted case; but it is still strong enough to allow a suitable version of the Strong Law of Large Numbers to hold. This result can be applied to prove a weak convergence result of interest in data analysis.

1. In this paper, the author derives a formula of inversion for the integral transform

where a > 0, k > 0. The actual formula obtained appears as equation (8) of the present paper and is deduced from an integral formula constructed in (1).

This paper continues (and concludes) the mathematical analysis begun in (8) of a formal theory of viscous flow in channels with slowly curving walls. In that paper, the theory was shown to yield strict asymptotic expansions, in powers of the small curvature parameter, of exact solutions of the Navier-Stokes equations, but the proofs were restricted to a set of Reynolds numbers and wall divergence angles that is distinctly smaller than the set on which the formal approximation is defined. In the present paper, we study in more detail a certain linear, partial differential operator TN, the invertibility of which is essential to the proofs. This operator is shown to be invertible (and the formal theory is thereby justified) on a parameter domain that is much larger than and may well be the whole of . A key step is to associate with TN a family of operators that approximate TN locally and have much simpler coefficients.

The concept of ideal strength of perfect crystals as an instability phenomenon is critically reviewed in the context of generalized moduli associated with arbitrary measures of stress and strain. Further aspects of elastic response to finite strain are discussed in relation to the classical model of an atomic lattice.